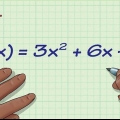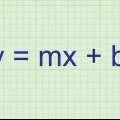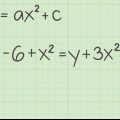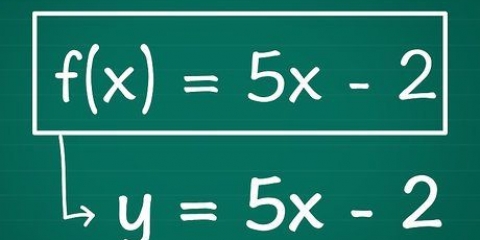As die waarde van a positief is, kry jy die minimum waarde, want die parabool aan die bokant is oop (die hoekpunt is die laagste punt van die grafiek).
As die waarde van a negatief is, sal jy die maksimum waarde vind, want die parabool aan die onderkant is oop (die hoekpunt is die hoogste punt van die grafiek).
Die waarde van a kan nie nul wees nie, anders het ons nie te doen met `n kwadratiese vergelyking nie, reg?







Bepaling van die maksimum en minimum waardes van 'n kwadratiese funksie
Inhoud
Die y-koördinaat van die kruin of vallei van `n parabool (gewoonlik voorgestel deur k) is ook die maksimum of minimum waarde van die kwadratiese vergelyking soos voorgestel deur die parabool. Kom ons kyk hoe om dit te bepaal!
Trappe
Metode 1 van 4: Vir `n kwadratiese vergelyking van die vorm y = ax + bx + c

1. Besluit of jy die maksimum waarde of die minimum waarde wil bepaal. Dit is die een of die ander, jy kan nie albei doen nie.
- Die maksimum of minimum waarde van `n kwadratiese vergelyking is dieselfde as die piek of vallei van daardie funksie.
Die funksie y = ax + bx + c,
(c - b/4a) gee die y-waarde (die waarde van die funksie) as die hoekpunt terug.




Metode 2 van 4: Vir `n kwadratiese vergelyking in die vorm y = a(x-h) + k

1. Vir y = a(x-h) + k, k is die waarde van die funksie by die hoekpunt.
- k gee ons die maksimum of minimum waarde van die kwadratiese vergelyking wanneer a is onderskeidelik negatief of positief.

Metode 3 van 4: Differensieer op `n kwadratiese vergelyking van die vorm y = ax^2 + bx + c

1. Onderskei y vir x. dy/dx = 2ax + b

2. Bepaal wat die afgeleide waardes is in terme van dy/dx. Aangesien dy/dx die afgeleide funksie van `n kromme is, kan die afgeleide van `n kromme op enige gegewe tydstip bepaal word. Die maksimum/minimum waarde kan dus bepaal word deur hierdie waardes gelyk aan 0 te stel, en dan die ooreenstemmende waardes te bepaal. dy/dx = 0, 2ax+b = 0, x = -b/2a

3. Vervang hierdie waarde van x in y vir die minimum/maksimum waarde.
Metode 4 van 4: Voorbeelde

1. Bepaal die maksimum of minimum waarde van die funksie f(x) = x + x + 1.

2. Bepaal die maksimum of minimum waarde van die funksie f(x) = -2(x-1) + 3.
Wenke
- Die simmetrie-as van die parabool is x = h.
- -h is die waarde wat ooreenstem met die maksimum of minimum waarde.
Artikels oor die onderwerp "Bepaling van die maksimum en minimum waardes van 'n kwadratiese funksie"
Оцените, пожалуйста статью
Soortgelyk
Gewilde