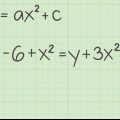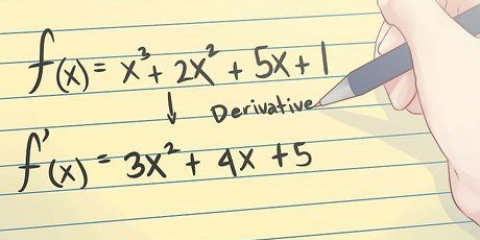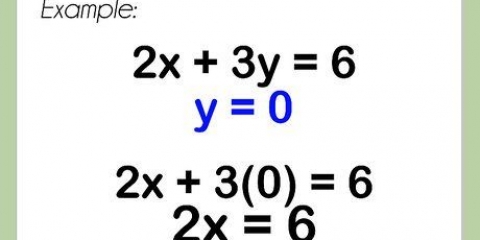Vind die omgekeerde van 'n funksie: 5 stappe (met prente)

Inhoud

Trappe
Wenke

`n Funksie in wiskunde (gewoonlik aangedui as f(x)) kan beskou word as `n soort formule of program waar jy `n waarde invoer "X" steek in, wat dan `n gegewe waarde vir gee y. Die omgekeerde van `n funksie f(x) (aangedui as f(x)) is in wese die omgekeerde: voer a in y-waarde en jy kry hoe vroeër X-waarde terug. Om die inverse van `n funksie te vind mag dalk ingewikkeld lyk, maar vir eenvoudige vergelykings, al wat jy nodig het is `n bietjie kennis van die basiese bewerkings in algebra. Lees die volgende stap-vir-stap instruksies en kyk mooi na die voorbeeld.

Trappe

Prent getiteld Algebraïes Vind die omgekeerde van `n funksie Stap 01

1. Skryf jou funksie deur f(x) te ruil met y Indien nodig. Jou formule behoort y om aan die een kant van die gelykheidsteken te hê en aan die ander kant die X-terme. As jy reeds `n vergelyking ingeskryf het y en X terme (soos byvoorbeeld 2 + y = 3x), dan benodig jy net y om opgelos te word deur dit te isoleer.

Voorbeeld: Ons het `n funksie f(x) = 5x - 2, en herskryf dit as y = 5x - 2, eenvoudig deur "f(x)" vervang te word deur y.
Let wel: f(x) is die standaardfunksienotasie, maar as jy met veelvuldige funksies te doen het, sal elke funksie `n ander beginletter kry om dit makliker te maak om hulle te onderskei. Byvoorbeeld, g(x) en h(x) is algemeen gebruikte letters vir funksies.

Prent getiteld Algebraïes Vind die omgekeerde van `n funksie Stap 02

2. los X aan. Met ander woorde, doen die nodige wysigings aan X om aan die een kant van die gelykheidsteken te isoleer. Om dit te doen, gebruik die basiese bewerkings van algebra: if X het `n koëffisiënt (`n getal vir die veranderlike), deel beide kante van die vergelyking deur hierdie getal om dit uit te kanselleer; is daar `n konstante binne die "X"-term, werk dit dan uit deur albei kante van die gelykheidsteken op te tel of af te trek, ensovoorts.

Onthou dat elke bewerking aan die een kant van die gelykheidsteken ook aan die ander kant gedoen moet word.

Voorbeeld: Om met ons voorbeeld voort te gaan, voeg ons eers 2 aan beide kante van die vergelyking by. Dit gee ons y + 2 = 5x. Dan deel ons beide kante van die vergelyking deur 5 en laat (y + 2)/5 = x. Ten slotte, om dit meer leesbaar te maak, herskryf ons die vergelyking met die "X" aan die linkerkant: x = (y + 2)/5.

Prent getiteld Algebraïes Vind die omgekeerde van `n funksie Stap 03

3. Ruil die veranderlikes om. Ruil X van y en omgekeerd. Die gevolglike vergelyking is die inverse van die oorspronklike funksie. Met ander woorde, as ons `n waarde het vir X vul ons oorspronklike vergelyking in, dan kan ons die antwoord in die omgekeerde invul (weer vir "X") wat die oorspronklike waarde terugstuur!

Voorbeeld: Nadat ons x en y omgeruil het, kry ons y = (x + 2)/5

Prent getiteld Algebraïes Vind die omgekeerde van `n funksie Stap 04

4. vervang y deur middel van "f(x)". Inverse funksies word gewoonlik aangedui as f(x) = (x terme) . Onthou dat die eksponent -1 in hierdie geval nie beteken dat ons `n eksponensiële bewerking op die funksie moet uitvoer nie. Dit is net `n manier om aan te dui dat hierdie funksie die omgekeerde van die oorspronklike is.

Omdat X gelyk is aan 1/x, kan jy ook f(x) skryf as "1/f(x)," `n ander notasie vir die inverse van f(x).

Prent getiteld Algebraïes Vind die omgekeerde van `n funksie Stap 05

5. Gaan jou werk na. Probeer om `n konstante in die oorspronklike funksie in te vul vir X. As jy die korrekte inverse vind, sal jy die oorspronklike waarde van vind "X" moet dit weer sien, as jy die resultaat hiervan in die omgekeerde invoer.

Voorbeeld: Kom ons voer 4 in as die waarde van X in ons oorspronklike vergelyking. Dit gee ons f(x) = 5(4) - 2, of f(x) = 18.

Vervolgens gaan ons hierdie resultaat in die omgekeerde invoer. Dus vervang ons 18 in die inverse funksie as die waarde van X. Deur dit te doen kry ons y = (18 + 2)/5 as gevolg en dit is gelyk aan y = 4. So 4 is die x-waarde waarmee ons begin het en daarmee weet ons ons het die regte inverse funksie gevind.

Wenke

Jy kan beide notasies f(x) = y en f^(-1)(x) = y sonder enige probleme gebruik as jy wiskundige bewerkings op die funksies doen. Maar dit is beter om die oorspronklike funksie en die inverse funksie uitmekaar te hou, so probeer om dit in algemene notasie te hou. In die geval van die inverse funksie die notasie f^(-1)(x).
Let daarop dat die inverse van `n funksie gewoonlik `n funksie self is, maar nie altyd nie.