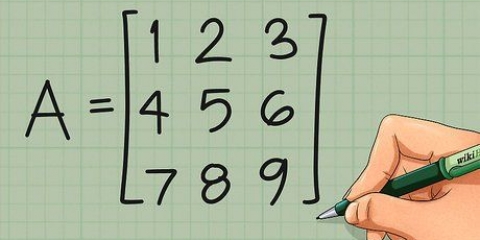Vind die inverse van 'n 3x3-matriks: 6 stappe (met prente)

Inhoud

Trappe
Wenke
Waarskuwings

Om die inverse van `n 3x3-matriks met die hand te bereken is `n vervelige taak. Maar dit is ook nuttig en nie moeilik nie, en dit help om verskeie matriksvergelykings op te los.

Trappe

1. Bepaal det(M), die determinant van die Matriks M. Die determinant is gewoonlik in die noemer van die inverse. As die determinant gelyk is aan nul, dan het die matriks geen inverse nie.

2. Bepaal M, die transposisie van die matriks. Om te transponeer beteken om die matriks in die hoofdiagonaal te weerspieël of wat ook al dieselfde is, deur die (i,j)-element en die (j,i)-element om te ruil.

3. Bepaal die determinant van elk van die minderjarige 2x2-matrikse, die minderjariges.

4. Vertoon dit as `n matriks van kofaktore soos aangedui, en vermenigvuldig elke term met die aangeduide teken.Die resultaat van hierdie stappe is die byvoegingsmatriks (soms ook byvoegingsmatriks), geskryf as Adj(M).

5. Vind die inverse deur die adjuvansmatriks wat in die vorige stap gevind is, te deel deur die determinant van die eerste stap.

6. Hierdie stappe kan gekombineer word deur te transponeer, oor die eerste twee rye en kolomme te kopieer en die 2x2 determinant rondom elke punt te bepaal. Deur die werk na te gaan, word die determinant op drie maniere bereken; as hierdie ooreenstem, dan het jy die korrekte antwoord gevind. Met die "torus" metode, is die teken onmiddellik korrek.

Wenke

Let daarop dat dieselfde metode toegepas kan word op `n matriks van veranderlikes en onbekendes, byvoorbeeld `n algebraïese matriks, M, en sy inverse, M.
Skryf al jou stappe neer, want dit is baie moeilik om die inverse van `n 3x3-matriks uit die kop op te los. Daarbenewens verseker neerskryf dat jy minder vinnig foute maak.
Daar is rekenaarprogramme wat die inverse van `n matriks vir jou bereken. , tot `n grootte van 30x30 matrikse

Die adjuvante matriks is die transponering van die matriks van kofaktore. Dit is hoekom ons die matriks in stap 2 transponeer om `n transposisie van `n kofaktormatriks te vind.
Kontroleer of dit korrek is wanneer M met M vermenigvuldig word. Jy behoort nou te kan bevestig dat M*M = M*M = I. I is die eenheidsmatriks, wat bestaan uit ene langs die hoofhoeklyn en nulle oral anders. Indien nie, het jy iewers `n fout gemaak.

Waarskuwings

Nie elke 3x3-matriks het `n inverse nie. As die determinant van die matriks 0 is, het dit geen inverse nie. (Let daarop dat ons in die formule deel deur det(M). Deel deur nul is nie moontlik nie.)