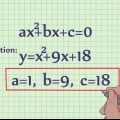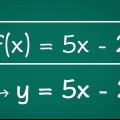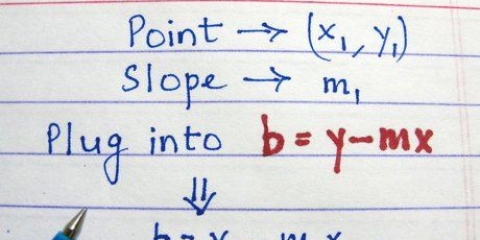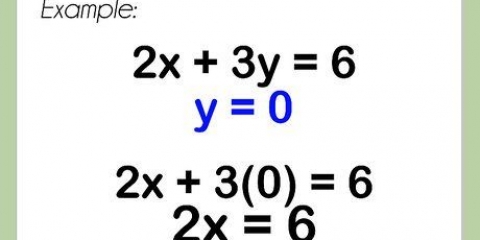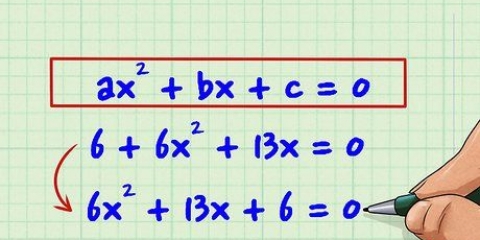Neem die voorbeeld vergelyking  , waar die y-terme na links geskuif kan word deur `n y van beide kante af te trek. Die ander terme kan na die regterkant geskuif word deur 6 aan beide kante by te voeg en
, waar die y-terme na links geskuif kan word deur `n y van beide kante af te trek. Die ander terme kan na die regterkant geskuif word deur 6 aan beide kante by te voeg en  van beide kante af te trek. Die gevolglike vergelyking is
van beide kante af te trek. Die gevolglike vergelyking is  .
. 
Kyk na die voorbeeldvergelyking  . Daar is geen beperking op die toegelate waardes van x vir hierdie vergelyking nie. Jy moet egter besef dat dit die vergelyking van `n parabool is, met x=0 as middelpunt, en `n parabool is nie `n funksie nie, want dit is nie `n een-tot-een vergelyking van x- en y-waardes. Om hierdie vergelyking te beperk en dit `n funksie te maak waarvoor ons `n inverse kan vind, moet ons die domein as x≥0 definieer.
. Daar is geen beperking op die toegelate waardes van x vir hierdie vergelyking nie. Jy moet egter besef dat dit die vergelyking van `n parabool is, met x=0 as middelpunt, en `n parabool is nie `n funksie nie, want dit is nie `n een-tot-een vergelyking van x- en y-waardes. Om hierdie vergelyking te beperk en dit `n funksie te maak waarvoor ons `n inverse kan vind, moet ons die domein as x≥0 definieer. Die reeks is op dieselfde manier beperk. Let daarop dat die eerste kwartaal,  , sal altyd positief of 0 wees, vir enige waarde van x. As die vergelyking dan +2 byvoeg, sal die reeks enige waarde y≥2 wees.
, sal altyd positief of 0 wees, vir enige waarde van x. As die vergelyking dan +2 byvoeg, sal die reeks enige waarde y≥2 wees. Dit is nodig om die domein en omvang in hierdie vroeë stadium te definieer. Jy sal hierdie definisies later gebruik wanneer jy die domein en omvang van die inverse funksie definieer. Trouens, die domein van die oorspronklike funksie word die omvang van die inverse funksie, en die omvang van die oorspronklike funksie word die domein van die inverse. 
Werk met die voorbeeldvergelyking  , hierdie inversiestap sal lei tot die nuwe vergelyking van
, hierdie inversiestap sal lei tot die nuwe vergelyking van  .
. `n Alternatiewe formaat is om die y-terme met x te vervang, maar die x-terme met een van die twee te vervang  of
of  om die inverse funksie aan te dui.
om die inverse funksie aan te dui. 
 (oorspronklike uitgangspunt)
(oorspronklike uitgangspunt) (trek 2 van beide kante af)
(trek 2 van beide kante af) (deel beide kante deur 2)
(deel beide kante deur 2)± (vierkantswortel van beide kante; onthou dat die vierkantswortel beide positiewe en negatiewe moontlike antwoorde tot gevolg het)
(vierkantswortel van beide kante; onthou dat die vierkantswortel beide positiewe en negatiewe moontlike antwoorde tot gevolg het) 
Sien die oplossing van die voorbeeldvergelyking ± . Aangesien die vierkantswortelfunksie nie vir negatiewe waardes gedefinieer is nie, moet die term . wees
. Aangesien die vierkantswortelfunksie nie vir negatiewe waardes gedefinieer is nie, moet die term . wees  wees altyd positief. Daarom moet die toegelate waardes van x (die domein) x≥2 wees. Met dit as die domein, is die resulterende waardes van y (die reeks) óf alle waardes y≥0, as jy die positiewe oplossing van die vierkantswortel neem, of y≤0, as jy die negatiewe oplossing van neem die vierkantswortel. Let daarop dat om die inverse funksie te vind, jy oorspronklik die domein as x≥0 gedefinieer het. Daarom is die korrekte oplossing vir die inverse funksie die positiewe opsie.
wees altyd positief. Daarom moet die toegelate waardes van x (die domein) x≥2 wees. Met dit as die domein, is die resulterende waardes van y (die reeks) óf alle waardes y≥0, as jy die positiewe oplossing van die vierkantswortel neem, of y≤0, as jy die negatiewe oplossing van neem die vierkantswortel. Let daarop dat om die inverse funksie te vind, jy oorspronklik die domein as x≥0 gedefinieer het. Daarom is die korrekte oplossing vir die inverse funksie die positiewe opsie. Vergelyk die domein en omvang van die inverse met die domein en omvang van die oorspronklike. Onthou dit vir die oorspronklike funksie,  , die domein is gedefinieer as alle waardes van x≥0, en die reeks is gedefinieer as alle waardes van y≥2. Vir die omgekeerde funksie, ruil hierdie waardes nou om, en die domein is alle waardes van x≥2, en die reeks is alle waardes van y≥0.
, die domein is gedefinieer as alle waardes van x≥0, en die reeks is gedefinieer as alle waardes van y≥2. Vir die omgekeerde funksie, ruil hierdie waardes nou om, en die domein is alle waardes van x≥2, en die reeks is alle waardes van y≥0. 
As `n voorbeeld, kies die waarde x=1 vir die oorspronklike vergelyking  . Dit gee die resultaat y=4.
. Dit gee die resultaat y=4. Dan plaas jy die waarde 4 in die inverse funksie  . Dit gee inderdaad die resultaat y=1. Jy kan aflei dat jou inverse funksie korrek is.
. Dit gee inderdaad die resultaat y=1. Jy kan aflei dat jou inverse funksie korrek is. 

Let daarop dat hierdie standaardvorm uit `n perfekte kwadratiese term bestaan,  , wat dan deur die ander twee elemente a en k verander word. Om by hierdie perfekte kwadratiese vorm uit te kom, sal jy sekere voorwaardes in jou kwadratiese vergelyking moet skep.
, wat dan deur die ander twee elemente a en k verander word. Om by hierdie perfekte kwadratiese vorm uit te kom, sal jy sekere voorwaardes in jou kwadratiese vergelyking moet skep. 
Om die vierkant te voltooi, werk omgekeerd. Jy begin met  en `n tweede x-termyn. Van die koëffisiënt van daardie term, wat jy as `2b` kan definieer, moet jy kry
en `n tweede x-termyn. Van die koëffisiënt van daardie term, wat jy as `2b` kan definieer, moet jy kry  sien om te vind. Dit vereis `n kombinasie van deling deur twee en dan die resultaat kwadraat.
sien om te vind. Dit vereis `n kombinasie van deling deur twee en dan die resultaat kwadraat. 
Neem byvoorbeeld die kwadratiese funksie  . Jy kan dit vereenvoudig deur alle terme deur 2 te deel om die resulterende funksie te kry
. Jy kan dit vereenvoudig deur alle terme deur 2 te deel om die resulterende funksie te kry  om te kry. Die koëffisiënt 2 bly buite die hakies en sal deel wees van jou finale oplossing.
om te kry. Die koëffisiënt 2 bly buite die hakies en sal deel wees van jou finale oplossing. As alle terme nie veelvoude van a is nie, kry jy breukkoëffisiënte. Byvoorbeeld: die funksie  sal vereenvoudig word om
sal vereenvoudig word om  . Werk die breuke versigtig uit.
. Werk die breuke versigtig uit. 
Byvoorbeeld, as die eerste twee terme van jou kwadratiese funksie  jy vind die nodige derde term deur 3 deur 2 (of 3/2) te deel en dit dan te kwadraat, om 9/4 te kry. Die kwadratiese
jy vind die nodige derde term deur 3 deur 2 (of 3/2) te deel en dit dan te kwadraat, om 9/4 te kry. Die kwadratiese  is `n perfekte vierkant.
is `n perfekte vierkant. Nog `n voorbeeld: veronderstel die eerste twee terme  is. Die helfte van die middelterm is -2, en dan vier jy dit om 4 te kry. Die gevolglike perfekte vierkant is
is. Die helfte van die middelterm is -2, en dan vier jy dit om 4 te kry. Die gevolglike perfekte vierkant is  .
. 
Gestel jy het die funksie  . Soos hierbo genoem, gebruik jy die eerste twee terme om die vierkant te voltooi. Deur die middelterm van -4x te gebruik, genereer jy `n derde term +4. Tel 4 by en trek 4 af van die vergelyking, in die vorm
. Soos hierbo genoem, gebruik jy die eerste twee terme om die vierkant te voltooi. Deur die middelterm van -4x te gebruik, genereer jy `n derde term +4. Tel 4 by en trek 4 af van die vergelyking, in die vorm  . Die hakies word slegs geplaas om die kwadratiese vergelyking wat jy maak, te definieer. Let op die +4 binne die hakies en die -4 aan die buitekant. Vereenvoudig die getalle tot die resultaat
. Die hakies word slegs geplaas om die kwadratiese vergelyking wat jy maak, te definieer. Let op die +4 binne die hakies en die -4 aan die buitekant. Vereenvoudig die getalle tot die resultaat  .
. 
Let daarop dat vir hierdie funksie a=1, h=2 en k=5. Die waarde van die skryf van die vergelyking in hierdie vorm is dat `n, omdat dit positief is, dit vir jou sê dat die parabool na bo wys. Die waardes (h, k) dui die hoekpunt aan die onderkant van die parabool aan, as jy dit wil teken. 
Gaan voort om met die voorskoufunksie te werk  . Aangesien dit in standaardformaat is, kan jy die hoekpunt as x=2, y=5 bepaal. Dus om die simmetrie te vermy, werk jy net met die regterkant van die grafiek, en stel die domein as alle waardes x≥2. Deur die waarde x=2 in die funksie in te voeg, gee dit y=5. Jy kan sien dat die waardes van y sal toeneem soos x toeneem. Daarom is die omvang van hierdie vergelyking y≥5.
. Aangesien dit in standaardformaat is, kan jy die hoekpunt as x=2, y=5 bepaal. Dus om die simmetrie te vermy, werk jy net met die regterkant van die grafiek, en stel die domein as alle waardes x≥2. Deur die waarde x=2 in die funksie in te voeg, gee dit y=5. Jy kan sien dat die waardes van y sal toeneem soos x toeneem. Daarom is die omvang van hierdie vergelyking y≥5. 
Gaan voort om met die funksie te werk  . Voeg x in die plek van f(x), en voeg y (of f(x), as jy verkies) in in die plek van x. Dit gee as `n nuwe funksie
. Voeg x in die plek van f(x), en voeg y (of f(x), as jy verkies) in in die plek van x. Dit gee as `n nuwe funksie  .
. 
 (oorspronklike beginpunt)
(oorspronklike beginpunt) (trek 5 van beide kante af)
(trek 5 van beide kante af)± (vierkantswortel van beide kante; onthou dat die vierkantswortel beide positiewe en negatiewe moontlike antwoorde lewer)
(vierkantswortel van beide kante; onthou dat die vierkantswortel beide positiewe en negatiewe moontlike antwoorde lewer) ± (voeg 2 by aan beide kante)
(voeg 2 by aan beide kante) 
Sien die oplossing van die voorbeeldvergelyking ± . Aangesien die vierkantswortelfunksie nie vir negatiewe waardes gedefinieer is nie, moet die term . wees
. Aangesien die vierkantswortelfunksie nie vir negatiewe waardes gedefinieer is nie, moet die term . wees  wees altyd positief. Daarom moet die toegelate waardes van x (die domein) x≥5 wees. Met dit as die domein, is die resulterende waardes van y (die reeks) óf alle waardes y≥2 (as jy die positiewe oplossing van die vierkantswortel neem), óf y≤2 (as jy die negatiewe oplossing kies van die vierkantswortel). Onthou dat jy oorspronklik die domein as x≥2 gedefinieer het, om die inverse funksie te vind. Daarom is die korrekte oplossing vir die inverse funksie die positiewe opsie.
wees altyd positief. Daarom moet die toegelate waardes van x (die domein) x≥5 wees. Met dit as die domein, is die resulterende waardes van y (die reeks) óf alle waardes y≥2 (as jy die positiewe oplossing van die vierkantswortel neem), óf y≤2 (as jy die negatiewe oplossing kies van die vierkantswortel). Onthou dat jy oorspronklik die domein as x≥2 gedefinieer het, om die inverse funksie te vind. Daarom is die korrekte oplossing vir die inverse funksie die positiewe opsie. Vergelyk die domein en omvang van die inverse met die domein en omvang van die oorspronklike. Onthou dat die domein vir die oorspronklike funksie gedefinieer is as alle waardes van x≥2, en die reeks is gedefinieer as alle waardes van y≥5. Vir hierdie inverse funksie ruil hierdie waardes om, en die domein is nou alle waardes van x≥5, en die reeks is alle waardes van y≥2. 
As `n voorbeeld, kies die waarde x=3 om in die oorspronklike vergelyking in te sluit  te verwerk. Dit gee die resultaat y=6.
te verwerk. Dit gee die resultaat y=6. Dan verwerk jy y=6 in die inverse funksie  . Dit gee y=3 terug, wat die getal is waarmee jy begin het. Jy kan aflei dat jou inverse funksie korrek is.
. Dit gee y=3 terug, wat die getal is waarmee jy begin het. Jy kan aflei dat jou inverse funksie korrek is. 

Vir hierdie afdeling van hierdie artikel sal jy die voorbeeldvergelyking gebruik  .
. 

Gebaseer op die werkvergelyking  , gee dit die resultaat
, gee dit die resultaat  .
. 
Vir die voorbeeldvergelyking, om die linkerkant gelyk aan nul te kry, moet jy x van albei kante van die vergelyking aftrek. Dit gee die resultaat  .
. 
Verlaat  . Dus, x=1
. Dus, x=1 Verlaat  . Dus, b=2
. Dus, b=2 Verlaat  . Dus, c=(-3-x)
. Dus, c=(-3-x) 
x=[-b±√(b^2-4ac)]/2a x=(-2)±√((-2)^2-4(1)(-3-x)) / 2(1) x=((-2)±√(4+12+4x)))/2 x=(-2±√(16+4x))/2 x=(-2±√(4)(4+x)))/2 x=-2±2√(4+x))/2 x=-1±√(4+x) f-inverse = -1±√(4+x)(Hierdie laaste stap is moontlik omdat jy f(x) op `n vroeër stadium vir die veranderlike x verruil het). 




Aanvaar die oorspronklike funksie  , kies jou x=-2. Dit gee y=-3 terug. Vervang nou die waarde van x=-3 in die inverse funksie,
, kies jou x=-2. Dit gee y=-3 terug. Vervang nou die waarde van x=-3 in die inverse funksie,  . Dit gee -2 terug, wat inderdaad die waarde is waarmee jy begin het. So jou definisie van die inverse funksie is korrek.
. Dit gee -2 terug, wat inderdaad die waarde is waarmee jy begin het. So jou definisie van die inverse funksie is korrek.
Vind die inverse van 'n kwadratiese vergelyking
Inhoud
Inverse funksies kan baie nuttig wees om baie wiskundeprobleme op te los. Om `n funksie te neem en die omgekeerde funksie daarvan te vind, is `n kragtige hulpmiddel. Met kwadratiese vergelykings kan dit egter nogal `n ingewikkelde proses wees. Eerstens moet jy die vergelyking noukeurig definieer deur `n toepaslike domein en reeks te bepaal. Jy het dan `n keuse van drie metodes om die inverse funksie te bereken. Die keuse van metode is hoofsaaklik `n kwessie van persoonlike voorkeur.
Trappe
Metode 1 van 3: Vind die inverse van `n eenvoudige funksie

1. Vind `n funksie in die vorm van y = a X 2 + c  . As jy die `regte` soort funksie het om mee te begin, kan jy die inverse vind met een of ander eenvoudige algebra. Hierdie vorm is `n soort variasie op
. As jy die `regte` soort funksie het om mee te begin, kan jy die inverse vind met een of ander eenvoudige algebra. Hierdie vorm is `n soort variasie op  . As jy dit vergelyk met `n standaard kwadratiese funksie,
. As jy dit vergelyk met `n standaard kwadratiese funksie,  , sien dat die middeltermyn
, sien dat die middeltermyn  is weg. Nog `n manier om dit te sê is dat die waarde van b nul is. As jou funksie hierdie vorm het, is dit redelik maklik om die inverse te vind.
is weg. Nog `n manier om dit te sê is dat die waarde van b nul is. As jou funksie hierdie vorm het, is dit redelik maklik om die inverse te vind.
 . As jy die `regte` soort funksie het om mee te begin, kan jy die inverse vind met een of ander eenvoudige algebra. Hierdie vorm is `n soort variasie op
. As jy die `regte` soort funksie het om mee te begin, kan jy die inverse vind met een of ander eenvoudige algebra. Hierdie vorm is `n soort variasie op  . As jy dit vergelyk met `n standaard kwadratiese funksie,
. As jy dit vergelyk met `n standaard kwadratiese funksie,  , sien dat die middeltermyn
, sien dat die middeltermyn  is weg. Nog `n manier om dit te sê is dat die waarde van b nul is. As jou funksie hierdie vorm het, is dit redelik maklik om die inverse te vind.
is weg. Nog `n manier om dit te sê is dat die waarde van b nul is. As jou funksie hierdie vorm het, is dit redelik maklik om die inverse te vind. - Jou aanvanklike funksie hoef nie presies so te lyk nie
. Solank jy daarna kan kyk en sien dat die funksie net bestaan uit
terme en konstante getalle, sal jy hierdie metode kan gebruik.
- Gestel jy begin met die vergelyking
. `n Vinnige ondersoek van hierdie vergelyking toon dat daar geen terme van
om tot die eerste mag te wees. Hierdie vergelyking is `n kandidaat vir hierdie metode om `n inverse funksie te vind.

2. Vereenvoudig deur soortgelyke terme te kombineer. Die aanvanklike vergelyking kan veelvuldige terme hê in `n kombinasie van optelling en aftrekking. Jou eerste stap is om soortgelyke terme te kombineer om die vergelyking te vereenvoudig en dit in die standaardformaat te herskryf  .
.
 .
. , waar die y-terme na links geskuif kan word deur `n y van beide kante af te trek. Die ander terme kan na die regterkant geskuif word deur 6 aan beide kante by te voeg en
, waar die y-terme na links geskuif kan word deur `n y van beide kante af te trek. Die ander terme kan na die regterkant geskuif word deur 6 aan beide kante by te voeg en  van beide kante af te trek. Die gevolglike vergelyking is
van beide kante af te trek. Die gevolglike vergelyking is  .
.
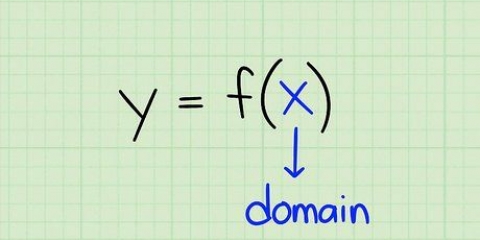
3. Bepaal die domein en omvang van die vereenvoudigde funksie. Onthou dat die domein van `n funksie bestaan uit die moontlike waardes van x wat toegepas kan word om `n werklike oplossing te gee. Die omvang van `n funksie bestaan uit die waardes van y wat sal terugkeer. Om die domein van die funksie te bepaal, soek waardes wat `n wiskundig onmoontlike resultaat lewer. Jy dui dan die domein aan as alle ander waardes van x. Om die reeks te vind, oorweeg die waardes van y by arbitrêre grenspunte en kyk na die gedrag van die funksie.
 . Daar is geen beperking op die toegelate waardes van x vir hierdie vergelyking nie. Jy moet egter besef dat dit die vergelyking van `n parabool is, met x=0 as middelpunt, en `n parabool is nie `n funksie nie, want dit is nie `n een-tot-een vergelyking van x- en y-waardes. Om hierdie vergelyking te beperk en dit `n funksie te maak waarvoor ons `n inverse kan vind, moet ons die domein as x≥0 definieer.
. Daar is geen beperking op die toegelate waardes van x vir hierdie vergelyking nie. Jy moet egter besef dat dit die vergelyking van `n parabool is, met x=0 as middelpunt, en `n parabool is nie `n funksie nie, want dit is nie `n een-tot-een vergelyking van x- en y-waardes. Om hierdie vergelyking te beperk en dit `n funksie te maak waarvoor ons `n inverse kan vind, moet ons die domein as x≥0 definieer. , sal altyd positief of 0 wees, vir enige waarde van x. As die vergelyking dan +2 byvoeg, sal die reeks enige waarde y≥2 wees.
, sal altyd positief of 0 wees, vir enige waarde van x. As die vergelyking dan +2 byvoeg, sal die reeks enige waarde y≥2 wees.
4. Ruil die rolle van die x- en y-terme om. Sonder om die vergelyking op enige ander manier te verander, moet jy alle vorme van y met x vervang, en alle vorme van x met y. Dit is die stap wat eintlik die vergelyking `omkeer`.
 , hierdie inversiestap sal lei tot die nuwe vergelyking van
, hierdie inversiestap sal lei tot die nuwe vergelyking van  .
. of
of  om die inverse funksie aan te dui.
om die inverse funksie aan te dui.
5. Herskryf die omgekeerde vergelyking in terme van y. Deur `n kombinasie van algebraïese stappe te gebruik en seker te maak dat dieselfde bewerking aan beide kante van die vergelyking uitgevoer word, sal jy die veranderlike y moet isoleer. Vir die vergelyking  , hierdie hersiening lyk soos volg:
, hierdie hersiening lyk soos volg:
 , hierdie hersiening lyk soos volg:
, hierdie hersiening lyk soos volg: (oorspronklike uitgangspunt)
(oorspronklike uitgangspunt) (trek 2 van beide kante af)
(trek 2 van beide kante af) (deel beide kante deur 2)
(deel beide kante deur 2) (vierkantswortel van beide kante; onthou dat die vierkantswortel beide positiewe en negatiewe moontlike antwoorde tot gevolg het)
(vierkantswortel van beide kante; onthou dat die vierkantswortel beide positiewe en negatiewe moontlike antwoorde tot gevolg het)
6. Bepaal die domein en omvang van die inverse funksie. Soos in die begin, ondersoek die omgekeerde vergelyking om die domein en omvang te bepaal. Met twee moontlike oplossings, kies die oplossing wat `n domein en reeks het wat die omgekeerde van die oorspronklike domein en reeks is.
 . Aangesien die vierkantswortelfunksie nie vir negatiewe waardes gedefinieer is nie, moet die term . wees
. Aangesien die vierkantswortelfunksie nie vir negatiewe waardes gedefinieer is nie, moet die term . wees  wees altyd positief. Daarom moet die toegelate waardes van x (die domein) x≥2 wees. Met dit as die domein, is die resulterende waardes van y (die reeks) óf alle waardes y≥0, as jy die positiewe oplossing van die vierkantswortel neem, of y≤0, as jy die negatiewe oplossing van neem die vierkantswortel. Let daarop dat om die inverse funksie te vind, jy oorspronklik die domein as x≥0 gedefinieer het. Daarom is die korrekte oplossing vir die inverse funksie die positiewe opsie.
wees altyd positief. Daarom moet die toegelate waardes van x (die domein) x≥2 wees. Met dit as die domein, is die resulterende waardes van y (die reeks) óf alle waardes y≥0, as jy die positiewe oplossing van die vierkantswortel neem, of y≤0, as jy die negatiewe oplossing van neem die vierkantswortel. Let daarop dat om die inverse funksie te vind, jy oorspronklik die domein as x≥0 gedefinieer het. Daarom is die korrekte oplossing vir die inverse funksie die positiewe opsie. , die domein is gedefinieer as alle waardes van x≥0, en die reeks is gedefinieer as alle waardes van y≥2. Vir die omgekeerde funksie, ruil hierdie waardes nou om, en die domein is alle waardes van x≥2, en die reeks is alle waardes van y≥0.
, die domein is gedefinieer as alle waardes van x≥0, en die reeks is gedefinieer as alle waardes van y≥2. Vir die omgekeerde funksie, ruil hierdie waardes nou om, en die domein is alle waardes van x≥2, en die reeks is alle waardes van y≥0.
7. Kyk of jou inverse funksie werk. Om seker te maak dat jou werk korrek is en jou inverse die korrekte vergelyking is, kies enige waarde vir x en plaas dit in die oorspronklike vergelyking om y te vind. Plaas dan daardie waarde van y in die plek van x in jou inverse vergelyking, en kyk of jy die getal kry waarmee jy begin het. Indien wel, is jou inverse funksie korrek.
 . Dit gee die resultaat y=4.
. Dit gee die resultaat y=4. . Dit gee inderdaad die resultaat y=1. Jy kan aflei dat jou inverse funksie korrek is.
. Dit gee inderdaad die resultaat y=1. Jy kan aflei dat jou inverse funksie korrek is.Metode 2 van 3: Voltooi die vierkant om die inverse funksie te vind

1. Gee die kwadratiese vergelyking die korrekte vorm. Om die inverse te vind, moet jy met die vergelyking van die vorm begin  . Indien nodig, moet jy soortgelyke terme kombineer om die vergelyking in hierdie formaat te kry. Met die vergelyking wat so geskryf is, kan jy `n bietjie meer daaroor vertel.
. Indien nodig, moet jy soortgelyke terme kombineer om die vergelyking in hierdie formaat te kry. Met die vergelyking wat so geskryf is, kan jy `n bietjie meer daaroor vertel.
 . Indien nodig, moet jy soortgelyke terme kombineer om die vergelyking in hierdie formaat te kry. Met die vergelyking wat so geskryf is, kan jy `n bietjie meer daaroor vertel.
. Indien nodig, moet jy soortgelyke terme kombineer om die vergelyking in hierdie formaat te kry. Met die vergelyking wat so geskryf is, kan jy `n bietjie meer daaroor vertel. - Die eerste ding wat jy sal opmerk is die waarde van die koëffisiënt a. As `n>0, dan definieer die vergelyking `n parabool waarvan die punte opwaarts wys (vallei-parabool). As `n<0, dan definieer die vergelyking `n parabool waarvan die punte afwaarts wys (bergparabool). Let daarop dat a≠0. As dit nie was nie, sou dit `n lineêre funksie wees en nie `n kwadratiese nie.

2. Herken die standaardformaat van die kwadratiese. Voordat jy die inverse funksie kan vind, moet jy die vergelyking in die standaardformaat herskryf. Die standaardformaat vir `n kwadratiese funksie is  . Die numeriese terme a, h en k sal geëvalueer word as jy die vergelyking transformeer deur die vierkant te bereken.
. Die numeriese terme a, h en k sal geëvalueer word as jy die vergelyking transformeer deur die vierkant te bereken.
 . Die numeriese terme a, h en k sal geëvalueer word as jy die vergelyking transformeer deur die vierkant te bereken.
. Die numeriese terme a, h en k sal geëvalueer word as jy die vergelyking transformeer deur die vierkant te bereken. , wat dan deur die ander twee elemente a en k verander word. Om by hierdie perfekte kwadratiese vorm uit te kom, sal jy sekere voorwaardes in jou kwadratiese vergelyking moet skep.
, wat dan deur die ander twee elemente a en k verander word. Om by hierdie perfekte kwadratiese vorm uit te kom, sal jy sekere voorwaardes in jou kwadratiese vergelyking moet skep.
3. Dink terug aan die vorm van `n perfekte kwadratiese funksie. Onthou dat `n kwadratiese funksie wat `n perfekte vierkant is, ontstaan uit twee binomiale van  , of
, of  . As jy hierdie vermenigvuldiging doen, kry jy
. As jy hierdie vermenigvuldiging doen, kry jy  . So die eerste term van die kwadratiese is die eerste term van die binomiaal, kwadraat, en die laaste term van die kwadratiese is die kwadraat van die tweede term van die binomiaal. Die middelterm bestaan uit twee keer die produk van die twee terme, in hierdie geval
. So die eerste term van die kwadratiese is die eerste term van die binomiaal, kwadraat, en die laaste term van die kwadratiese is die kwadraat van die tweede term van die binomiaal. Die middelterm bestaan uit twee keer die produk van die twee terme, in hierdie geval  .
.
 , of
, of  . As jy hierdie vermenigvuldiging doen, kry jy
. As jy hierdie vermenigvuldiging doen, kry jy  . So die eerste term van die kwadratiese is die eerste term van die binomiaal, kwadraat, en die laaste term van die kwadratiese is die kwadraat van die tweede term van die binomiaal. Die middelterm bestaan uit twee keer die produk van die twee terme, in hierdie geval
. So die eerste term van die kwadratiese is die eerste term van die binomiaal, kwadraat, en die laaste term van die kwadratiese is die kwadraat van die tweede term van die binomiaal. Die middelterm bestaan uit twee keer die produk van die twee terme, in hierdie geval  .
. en `n tweede x-termyn. Van die koëffisiënt van daardie term, wat jy as `2b` kan definieer, moet jy kry
en `n tweede x-termyn. Van die koëffisiënt van daardie term, wat jy as `2b` kan definieer, moet jy kry  sien om te vind. Dit vereis `n kombinasie van deling deur twee en dan die resultaat kwadraat.
sien om te vind. Dit vereis `n kombinasie van deling deur twee en dan die resultaat kwadraat.
4. Maak seker dat die koëffisiënt van X 2  1 is. Onthou jy die oorspronklike vorm van die kwadratiese funksie
1 is. Onthou jy die oorspronklike vorm van die kwadratiese funksie  . As die eerste koëffisiënt enigiets anders as 1 is, moet jy alle terme deur daardie waarde deel om a=1 te kry.
. As die eerste koëffisiënt enigiets anders as 1 is, moet jy alle terme deur daardie waarde deel om a=1 te kry.
 1 is. Onthou jy die oorspronklike vorm van die kwadratiese funksie
1 is. Onthou jy die oorspronklike vorm van die kwadratiese funksie  . As die eerste koëffisiënt enigiets anders as 1 is, moet jy alle terme deur daardie waarde deel om a=1 te kry.
. As die eerste koëffisiënt enigiets anders as 1 is, moet jy alle terme deur daardie waarde deel om a=1 te kry. . Jy kan dit vereenvoudig deur alle terme deur 2 te deel om die resulterende funksie te kry
. Jy kan dit vereenvoudig deur alle terme deur 2 te deel om die resulterende funksie te kry  om te kry. Die koëffisiënt 2 bly buite die hakies en sal deel wees van jou finale oplossing.
om te kry. Die koëffisiënt 2 bly buite die hakies en sal deel wees van jou finale oplossing. sal vereenvoudig word om
sal vereenvoudig word om  . Werk die breuke versigtig uit.
. Werk die breuke versigtig uit.
5. Vind die helfte van die middelste koëffisiënt en vierkant dit. Jy het reeds die eerste twee terme van die kwadratiese formule. Dit is die term  en die koëffisiënt wat die x-term verteenwoordig. Deur daardie koëffisiënt te neem as die waarde wat dit het, kan jy die getal wat nodig is om `n perfekte vierkant te maak, optel of aftrek. Onthou van bo af dat die vereiste derde term van die vierkant hierdie tweede koëffisiënt is gedeel deur twee, en dan kwadraat.
en die koëffisiënt wat die x-term verteenwoordig. Deur daardie koëffisiënt te neem as die waarde wat dit het, kan jy die getal wat nodig is om `n perfekte vierkant te maak, optel of aftrek. Onthou van bo af dat die vereiste derde term van die vierkant hierdie tweede koëffisiënt is gedeel deur twee, en dan kwadraat.
 en die koëffisiënt wat die x-term verteenwoordig. Deur daardie koëffisiënt te neem as die waarde wat dit het, kan jy die getal wat nodig is om `n perfekte vierkant te maak, optel of aftrek. Onthou van bo af dat die vereiste derde term van die vierkant hierdie tweede koëffisiënt is gedeel deur twee, en dan kwadraat.
en die koëffisiënt wat die x-term verteenwoordig. Deur daardie koëffisiënt te neem as die waarde wat dit het, kan jy die getal wat nodig is om `n perfekte vierkant te maak, optel of aftrek. Onthou van bo af dat die vereiste derde term van die vierkant hierdie tweede koëffisiënt is gedeel deur twee, en dan kwadraat. jy vind die nodige derde term deur 3 deur 2 (of 3/2) te deel en dit dan te kwadraat, om 9/4 te kry. Die kwadratiese
jy vind die nodige derde term deur 3 deur 2 (of 3/2) te deel en dit dan te kwadraat, om 9/4 te kry. Die kwadratiese  is `n perfekte vierkant.
is `n perfekte vierkant. is. Die helfte van die middelterm is -2, en dan vier jy dit om 4 te kry. Die gevolglike perfekte vierkant is
is. Die helfte van die middelterm is -2, en dan vier jy dit om 4 te kry. Die gevolglike perfekte vierkant is  .
.
6. Tel op en trek terselfdertyd af van die vereiste derde kwartaal. Dit is `n moeilike konsep, maar dit werk. Om dieselfde getal op verskillende plekke van jou funksie op te tel en af te trek, verander nie regtig die waarde van die funksie nie. Deur dit te doen sal jy egter jou funksie in behoorlike vorm kry.
 . Soos hierbo genoem, gebruik jy die eerste twee terme om die vierkant te voltooi. Deur die middelterm van -4x te gebruik, genereer jy `n derde term +4. Tel 4 by en trek 4 af van die vergelyking, in die vorm
. Soos hierbo genoem, gebruik jy die eerste twee terme om die vierkant te voltooi. Deur die middelterm van -4x te gebruik, genereer jy `n derde term +4. Tel 4 by en trek 4 af van die vergelyking, in die vorm  . Die hakies word slegs geplaas om die kwadratiese vergelyking wat jy maak, te definieer. Let op die +4 binne die hakies en die -4 aan die buitekant. Vereenvoudig die getalle tot die resultaat
. Die hakies word slegs geplaas om die kwadratiese vergelyking wat jy maak, te definieer. Let op die +4 binne die hakies en die -4 aan die buitekant. Vereenvoudig die getalle tot die resultaat  .
.
7. Faktoreer die kwadratiese vergelyking. Die polinoom tussen hakies is `n kwadratiese vergelyking, wat jy kan herskryf as  . In die voorbeeld van die vorige stap (
. In die voorbeeld van die vorige stap ( ) jy faktoreer die kwadratiese faktor in
) jy faktoreer die kwadratiese faktor in  . Kopieer die res van die vergelyking sodat jou oplossing
. Kopieer die res van die vergelyking sodat jou oplossing  word. Dit is dieselfde funksie as jou oorspronklike kwadratiese vergelyking (
word. Dit is dieselfde funksie as jou oorspronklike kwadratiese vergelyking ( ), herskryf as die standaardvorm
), herskryf as die standaardvorm  .
.
 . In die voorbeeld van die vorige stap (
. In die voorbeeld van die vorige stap ( ) jy faktoreer die kwadratiese faktor in
) jy faktoreer die kwadratiese faktor in  . Kopieer die res van die vergelyking sodat jou oplossing
. Kopieer die res van die vergelyking sodat jou oplossing  word. Dit is dieselfde funksie as jou oorspronklike kwadratiese vergelyking (
word. Dit is dieselfde funksie as jou oorspronklike kwadratiese vergelyking ( ), herskryf as die standaardvorm
), herskryf as die standaardvorm  .
.
8. Definieer die domein en omvang van die funksie. Die domein is die stel x-waardes wat as insette vir die funksie gebruik kan word. Die reeks is die stel y-waardes wat die resultaat kan wees. Onthou dat `n parabool nie `n funksie met `n definieerbare inverse is nie, want daar is geen een-tot-een verband tussen x-waardes en y-waardes nie, as gevolg van die simmetrie van die parabool. Om hierdie probleem op te los, moet jy die domein definieer as alle waardes van x wat groter is as x=h, die hoekpunt van die parabool.
 . Aangesien dit in standaardformaat is, kan jy die hoekpunt as x=2, y=5 bepaal. Dus om die simmetrie te vermy, werk jy net met die regterkant van die grafiek, en stel die domein as alle waardes x≥2. Deur die waarde x=2 in die funksie in te voeg, gee dit y=5. Jy kan sien dat die waardes van y sal toeneem soos x toeneem. Daarom is die omvang van hierdie vergelyking y≥5.
. Aangesien dit in standaardformaat is, kan jy die hoekpunt as x=2, y=5 bepaal. Dus om die simmetrie te vermy, werk jy net met die regterkant van die grafiek, en stel die domein as alle waardes x≥2. Deur die waarde x=2 in die funksie in te voeg, gee dit y=5. Jy kan sien dat die waardes van y sal toeneem soos x toeneem. Daarom is die omvang van hierdie vergelyking y≥5.
9. Ruil die x- en y-waardes om. Dit is die stap waar jy begin deur die inverse vorm van die vergelyking te vind. Los die vergelyking in sy geheel, behalwe om hierdie veranderlikes om te ruil.
 . Voeg x in die plek van f(x), en voeg y (of f(x), as jy verkies) in in die plek van x. Dit gee as `n nuwe funksie
. Voeg x in die plek van f(x), en voeg y (of f(x), as jy verkies) in in die plek van x. Dit gee as `n nuwe funksie  .
.
10. Herskryf die omgekeerde vergelyking in terme van y. Gebruik `n kombinasie van algebraïese stappe, maak seker dat jy dieselfde bewerking eweredig aan beide kante van die vergelyking uitvoer, isoleer die veranderlike y. Vir die werkvergelyking  hierdie hersiening lyk soos volg:
hierdie hersiening lyk soos volg:
 hierdie hersiening lyk soos volg:
hierdie hersiening lyk soos volg: (oorspronklike beginpunt)
(oorspronklike beginpunt) (trek 5 van beide kante af)
(trek 5 van beide kante af) (vierkantswortel van beide kante; onthou dat die vierkantswortel beide positiewe en negatiewe moontlike antwoorde lewer)
(vierkantswortel van beide kante; onthou dat die vierkantswortel beide positiewe en negatiewe moontlike antwoorde lewer) (voeg 2 by aan beide kante)
(voeg 2 by aan beide kante)
11. Bepaal die domein en omvang van die inverse funksie. Soos in die begin, ondersoek die omgekeerde vergelyking om die domein en omvang te bepaal. Met twee moontlike oplossings, kies die oplossing wat `n domein en reeks het wat die omgekeerde van die oorspronklike domein en reeks is.
 . Aangesien die vierkantswortelfunksie nie vir negatiewe waardes gedefinieer is nie, moet die term . wees
. Aangesien die vierkantswortelfunksie nie vir negatiewe waardes gedefinieer is nie, moet die term . wees  wees altyd positief. Daarom moet die toegelate waardes van x (die domein) x≥5 wees. Met dit as die domein, is die resulterende waardes van y (die reeks) óf alle waardes y≥2 (as jy die positiewe oplossing van die vierkantswortel neem), óf y≤2 (as jy die negatiewe oplossing kies van die vierkantswortel). Onthou dat jy oorspronklik die domein as x≥2 gedefinieer het, om die inverse funksie te vind. Daarom is die korrekte oplossing vir die inverse funksie die positiewe opsie.
wees altyd positief. Daarom moet die toegelate waardes van x (die domein) x≥5 wees. Met dit as die domein, is die resulterende waardes van y (die reeks) óf alle waardes y≥2 (as jy die positiewe oplossing van die vierkantswortel neem), óf y≤2 (as jy die negatiewe oplossing kies van die vierkantswortel). Onthou dat jy oorspronklik die domein as x≥2 gedefinieer het, om die inverse funksie te vind. Daarom is die korrekte oplossing vir die inverse funksie die positiewe opsie.
12. Kyk of jou inverse funksie werk. Om seker te maak dat jou werk korrek is en jou inverse die korrekte vergelyking is, kies enige waarde vir x en plaas dit in die oorspronklike vergelyking om y te vind. Plaas dan daardie waarde van y in die plek van x in jou inverse vergelyking, en kyk of jy die getal kry waarmee jy begin het. Indien wel, dan is jou inverse funksie korrek.
 te verwerk. Dit gee die resultaat y=6.
te verwerk. Dit gee die resultaat y=6. . Dit gee y=3 terug, wat die getal is waarmee jy begin het. Jy kan aflei dat jou inverse funksie korrek is.
. Dit gee y=3 terug, wat die getal is waarmee jy begin het. Jy kan aflei dat jou inverse funksie korrek is.Metode 3 van 3: Gebruik die vierkantige formule

1. Gebruik die kwadratiese formule om x op te los. Onthou, wanneer kwadratiese vergelykings opgelos word, is daar een metode om dit te faktoriseer (indien moontlik). As faktorisering nie gewerk het nie, kan jy die vierkantsformule gebruik, wat die werklike oplossings vir enige kwadratiese vergelyking sal gee. Jy kan ook die vierkantsformule gebruik as `n metode om inverse funksies te vind.
- Die vierkantige formule is x=[-b±√(b^2-4ac)]/2a.
- Let daarop dat die vierkantsformule twee moontlike oplossings gee, `n positiewe en `n negatiewe. Jy sal hierdie keuse maak op grond van die bepaling van die domein en omvang van die funksie.

2. Begin met `n kwadratiese vergelyking om die inverse te vind. Jou kwadratiese vergelyking moet in die formaat begin  . Neem die algebraïese stappe wat nodig is om jou vergelyking in daardie vorm te kry.
. Neem die algebraïese stappe wat nodig is om jou vergelyking in daardie vorm te kry.
 . Neem die algebraïese stappe wat nodig is om jou vergelyking in daardie vorm te kry.
. Neem die algebraïese stappe wat nodig is om jou vergelyking in daardie vorm te kry. .
.
3. Stip die vergelyking om die domein en omvang te bepaal. Teken die funksie in grafieke deur óf `n grafiese sakrekenaar te gebruik óf teken verskeie punte totdat jy die parabool kan teken. Jy sal sien dat hierdie vergelyking `n parabool definieer met die hoogste punt by (-1,-4). Dus om dit te definieer as `n funksie wat `n inverse sal hê, definieer jy die domein as alle waardes van x≤-1. Die reeks is dan alle waardes y≥-4.

4. Ruil die veranderlikes x en y om. Om die inverse te vind, ruil die veranderlikes x en y om. Laat die vergelyking onveranderd, behalwe om die veranderlikes om te ruil. Op hierdie stadium, vervang x met f(x).
 , gee dit die resultaat
, gee dit die resultaat  .
.
5. Stel die linkerkant van die vergelyking gelyk aan nul. Onthou dat om die kwadratiese formule te gebruik jy die vergelyking gelyk aan nul moet stel, gebruik dan die koëffisiënte in die formule. Net so begin hierdie metode om `n inverse funksie te vind deur die vergelyking gelyk aan nul te stel.
 .
.
6. Herdefinieer die veranderlikes om by die vierkantsformule te pas. Hierdie stap is `n bietjie moeilik. Weet dat die vierkantsformule vir x in die vergelyking oplos  . So, vir die vergelyking wat jy nou het,
. So, vir die vergelyking wat jy nou het,  , om aan daardie klassifikasie te voldoen, moet jy die terme soos volg herdefinieer:
, om aan daardie klassifikasie te voldoen, moet jy die terme soos volg herdefinieer:
 . So, vir die vergelyking wat jy nou het,
. So, vir die vergelyking wat jy nou het,  , om aan daardie klassifikasie te voldoen, moet jy die terme soos volg herdefinieer:
, om aan daardie klassifikasie te voldoen, moet jy die terme soos volg herdefinieer: . Dus, x=1
. Dus, x=1 . Dus, b=2
. Dus, b=2 . Dus, c=(-3-x)
. Dus, c=(-3-x)
7. Los die vierkantige formule op met hierdie herdefinieerde waardes. Normaalweg sal jy die waardes van a, b en c in die vierkantsformule verwerk om vir x op te los. Onthou egter dat jy voorheen x en y omgeruil het om die van die inverse funksie te vind. So wanneer jy die vierkantsformule gebruik om vir x op te los, los jy eintlik y op, of die f-inverse. Die stappe om die vierkantige formule op te los werk soos volg:

8. Skryf die twee moontlike oplossings neer. Let daarop dat die vierkantsformule twee moontlike uitkomste gee deur die ±-simbool te gebruik. Skryf die twee aparte oplossings neer om dit makliker te maak om die domein en omvang te bepaal en gee die korrekte finale oplossing. Hierdie twee oplossings is:



9. Bepaal die domein en omvang van die inverse funksie. Let daarop dat die domein x≥-4 moet wees om die vierkantswortel te definieer. Onthou dat die domein van die oorspronklike funksie x≤-1 was en die reeks was y≥-4. Om die inverse funksie te kies wat ooreenstem, benodig jy die tweede oplossing,  kies as die korrekte inverse funksie.
kies as die korrekte inverse funksie.
 kies as die korrekte inverse funksie.
kies as die korrekte inverse funksie.
10. Kyk of jou inverse funksie korrek is. Om seker te maak dat jou werk korrek is en jou inverse die korrekte vergelyking is, kies enige waarde vir x en plaas dit in die oorspronklike vergelyking om y te vind. Plaas dan daardie waarde van y in die plek van x in jou inverse vergelyking, en kyk of jy die getal kry waarmee jy begin het. Indien wel, dan is jou inverse funksie korrek.
 , kies jou x=-2. Dit gee y=-3 terug. Vervang nou die waarde van x=-3 in die inverse funksie,
, kies jou x=-2. Dit gee y=-3 terug. Vervang nou die waarde van x=-3 in die inverse funksie,  . Dit gee -2 terug, wat inderdaad die waarde is waarmee jy begin het. So jou definisie van die inverse funksie is korrek.
. Dit gee -2 terug, wat inderdaad die waarde is waarmee jy begin het. So jou definisie van die inverse funksie is korrek.Artikels oor die onderwerp "Vind die inverse van 'n kwadratiese vergelyking"
Оцените, пожалуйста статью
Soortgelyk
Gewilde