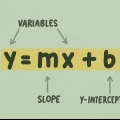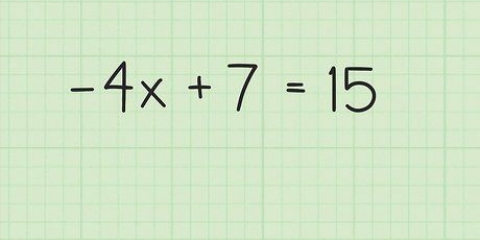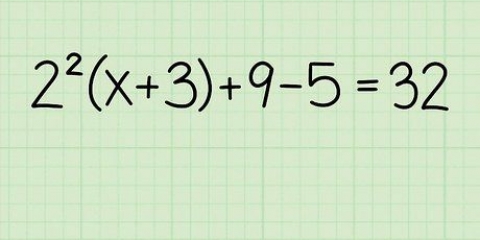Daar is `n punt en `n helling gegee. Twee punte word gegee, maar geen helling nie. Gegee `n punt en `n ander lyn parallel daaraan. Gegee `n punt en `n ander lyn loodreg daarop. 




Herrangskik jou vergelyking. b = y - mx. Voer die waardes in en los op. b = -5 - (2/3)6. b = -5 - 4. b = -9 Kontroleer dat die kruising met die y-as werklik -9 is. Skryf die vergelyking neer: y = 2/3 x - 9 

Gebruik jou helling en koördinate in die vergelyking hierbo. Vermenigvuldig die helling (m) met die x-koördinaat van die punt. Trek die waarde van die y-koördinaat van die punt af. jy het nou b opgelos, die kruising met die y-as. 



Bereken die helling. Die helling = (Y2 - Y1) / (X2 - X1) -12 - (-5) / 8 - 6 = -7 / 2 Die helling is -7/2 (van die eerste punt na die tweede gaan ons 7 af en 2 na regs, so die helling is -7 oor 2). Herrangskik jou vergelyking. b = y - mx. Voer die waardes in en los op. b = -12 - (-7/2)8. b = -12 - (-28). b = -12 + 28. b = 16 Opmerking: omdat ons die 8 vir die koördinate gebruik het, moet ons ook die -12 gebruik.As jy die 6 vir jou koördinate gebruik, moet jy ook die -5 gebruik. Maak seker dat jou kruising met die y-as werklik 16 is. Skryf die vergelyking neer: y = -7/2 x + 16 
Vervang die helling en koördinate in die bogenoemde vergelyking. Vermenigvuldig die helling (m) met die x-koördinaat van die punt. Trek die waarde van die y-koördinaat van die punt af. Jy het b opgelos, die kruising met die y-as. 


Los die helling op. Die helling van ons nuwe lyn sal dieselfde wees as die helling van die ou lyn. Bepaal die helling van die ou lyn: -2j = -5x + 1 trek "-2" van beide kante af: y = 5/2x - 1/2 Die helling is 5/2. Herrangskik jou vergelyking. b = y - mx. Vul in en los op. b = 3 - (5/2)4. b = 3 - (10). b = -7. Kyk of die kruising met die y-as werklik -7 is. Skryf die vergelyking neer: y = 5/2 x - 7 
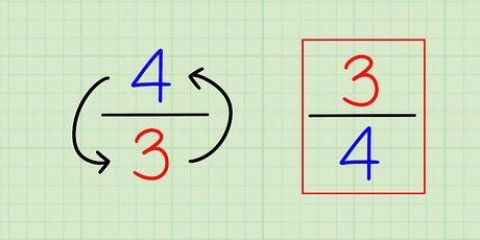
2/3 word -3/2 -6/5 word 5/6 3 (of 3/1 — is dieselfde) word -1/3 -1/2 word 2 
Koppel jou helling en koördinate in die vergelyking hierbo. Vermenigvuldig die helling (m) met die x-koördinaat van die punt. Trek daardie waarde af van die y-koördinaat van die punt. Jy het nou die vergelyking opgelos vir b; die kruising met die y-as. 


Los die helling op. Die helling van ons nuwe lyn word die negatiewe inverse van die helling van die ou lyn. Bepaal die helling van die ou lyn: 2j = -4x + 9 trek "2" van beide kante af: y = -4/2x + 9/2 Die helling is -4/2 of -2. Die negatiewe wederkerige van -2 is 1/2. herrangskik jou vergelyking. b = y - mx. Vul in en los op. b = -1 - (1/2)8. b = -1 - (4). b = -5. Kontroleer dat jou kruising met die y-as werklik -5 is. Skryf die vergelyking: y = 1/2 x - 5
Vind die vergelyking van 'n lyn
Inhoud
Om die vergelyking van `n lyn wat jy het te vind twee dinge nodig:a) `n punt op die lyn; en b) die helling (soms ook die helling) van die lyn. Maar hoe jy hierdie twee stukke inligting insamel en wat jy daarna daarmee doen, kan baie verskil na gelang van die situasie. Ter wille van eenvoud, sal hierdie artikel fokus op vergelykings van die vorm y = mx + b in plaas van (j-j1) = m(x - x1).
Trappe
Metode 1 van 5: Algemene inligting
1. Weet waarna om te kyk.Voordat jy die vergelyking kan soek, moet jy seker weet wat jy probeer vind. Hou die volgende in gedagte:
- Punte word geklassifiseer as bestelde paar, soos (-7, -8) of (-2,-6).
- Die eerste nommer in `n geordende paar is die x koördinaat. Dit is die horisontale posisie van die punt (hoeveel eenhede links of regs van die oorsprong).
- Die tweede nommer in `n geordende paar is die y koördinaat. Dit is die vertikale posisie van die punt (hoeveel eenhede op of af vanaf die oorsprong).
- Die gradiënt tussen die twee punte word die genoem "die helling" — met ander woorde, hoe ver jy op (of af) en regs (of links) moet gaan om van een punt na `n ander te kom.
- Twee lyne is parallel as hulle nie kruis nie.
- Twee reëls is loodreg op mekaar as hulle teen `n regte hoek (90 grade) sny.
2. Bepaal watter tipe opdrag jy te doen het.
3. Pak die probleem aan deur een van die vier metodes hieronder te gebruik. Afhangende van die inligting wat gegee word, is daar verskillende maniere om dit op te los.
Metode 2 van 5: `n Punt en `n helling word gegee

1. Vind die snypunt van jou vergelyking met die y-as. Die kruising met die y-as (of die veranderlike b in ons vergelyking) is die punt waar die lyn met die y-as sny. Jy kan die snypunt met die y-as bereken deur die vergelyking om op te los te herrangskik b. Ons nuwe vergelyking lyk nou so: b = y - mx.
- Voer jou helling en koördinate in in die vergelyking hierbo.
- Vermenigvuldig die helling (m) met die x-koördinaat van die punt.
- Trek daardie waarde af van die y-koördinaat van die punt.
- Nou het jy b opgelos, die kruising met die y-as.

2. Skryf die formule uit:y = ____ x + ____ , saam met die spasies.

3. Vul die eerste leë spasie in, die een vir die x, met die helling.

4. Vul die tweede spasie in met die kruising met die y-as wat jy voorheen bereken het.

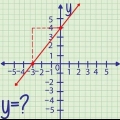
5. Los die voorbeeldprobleem op. "Gegewe die punt (6, -5) en die helling 2/3, wat is die vergelyking van die lyn?"
Metode 3 van 5:Twee punte word gegee
1. Bereken die helling tussen twee punte. Die helling word ook die gradiënt en jy kan hieraan dink as die tempo waarteen iets langs `n denkbeeldige y-as en x-as beweeg. Die vergelyking vir die helling is: (Y2 - Y1) / (X2 - X1)
- Neem die twee punte en gebruik hulle in die vergelyking (twee koördinate beteken twee y-waardes en twee X-waardes). Dit maak nie saak watter koördinate jy eerste invoer nie, solank jy dit konsekwent doen. Enkele voorbeelde:
- Punte (3, 8) en (7, 12). (Y2 - Y1) / (X2 - X1) = 12 - 8 / 7 - 3 = 4/4, of 1.
- Punte (5, 5) en (9, 2). (Y2 - Y1) / (X2 - X1) = 2 - 5 / 9 - 5 = -3/4.

2. Kies `n stel koördinate vir die res van die probleem. Trek die ander stel koördinate deur of bedek die ander stel koördinate sodat jy dit nie per ongeluk gebruik nie.

3. Bereken die snypunt met die y-as van jou vergelyking. Herrangskik weer die formule y = mx + b om `n vergelyking van die vorm b = y – mx te kry. Dit is steeds dieselfde vergelyking; jy het dit net herrangskik.

4. Skryf die formule uit:y = ____ x + ____ , insluitend die spasies.

5. Vul die eerste leë spasie in, die een vir die x, met die helling.

6. Vul die tweede spasie in met die kruising met die y-as.

7. Los die voorbeeldprobleem op. "Gegewe die punte (6, -5) en (8, -12), wat is die vergelyking van die lyn?"
Metode 4 van 5: Wanneer `n punt en `n parallelle lyn gegee word
1. Bepaal die helling van die parallelle lyn. Onthou dat die helling die koëffisiënt van is X waardeur y het geen koëffisiënt nie.
- In `n vergelyking soos y = 3/4 x + 7, is die helling 3/4.
- In `n vergelyking soos y = 3x - 2, is die helling 3.
- In `n vergelyking soos y = 3x, is die helling steeds 3.
- In `n vergelyking soos y = 7, is die helling nul (omdat daar nul x`e in die probleem is).
- In `n vergelyking soos y = x - 7, is die helling 1.
- In `n vergelyking soos -3x + 4y = 8, is die helling 3/4.
- Om die helling van `n vergelyking soos hierdie te vind, herrangskik dit net sodat die y is geïsoleer:
- 4j = 3x + 8
- Deel beide kante deur 4: y = 3/4x + 2

2. Bereken die snypunt met die y-as, gebruik die helling van die eerste stap en die vergelyking b = y - mx.

3. Skryf die formule neer:y = ____ x + ____ , met die spasies.

4. Vul die eerste leë spasie, voor die x, in met die helling wat jy in stap 1 bepaal het.Die merkwaardige ding van parallelle lyne is dat hulle dieselfde helling het, so jy eindig met wat jy begin het.

5. Vul die kruising met die y-as in die tweede leë spasie in.
6. Los die voorbeeldprobleem op. "Gegee die punt (4, 3) en die ewewydige lyn 5x - 2y = 1; wat is die vergelyking van die lyn?"
Metode 5 van 5: Met `n gegewe punt en `n loodregte lyn
1. Vind die helling van die gegewe lyn. Kyk na die voorbeelde hierbo vir meer inligting.

2. Vind die negatiewe wederkerige van daardie helling. Met ander woorde, draai dit om en verander die teken. Die punt met loodregte lyne is dat hulle `n negatiewe inverse helling het, so jy sal veranderinge aan die helling moet maak voordat jy dit kan gebruik.

3. Bereken die snypunt met die y-as deur die helling te gebruik vanaf stap 2 en die vergelyking b = y - mx

4. Skryf die formule neer:y = ____ x + ____ , met die spasies.

5. Vul die eerste leë spasie, voor die x, in met die helling wat jy in stap 2 bereken het.

6. Vul die kruising met die y-as in die tweede leë spasie in.
7. Los die voorbeeldprobleem op. "Gegee (8, -1) en en die loodregte 4x + 2y = 9; wat is die vergelyking van die lyn?"
Artikels oor die onderwerp "Vind die vergelyking van 'n lyn"
Оцените, пожалуйста статью
Soortgelyk
Gewilde