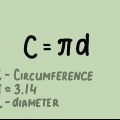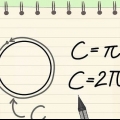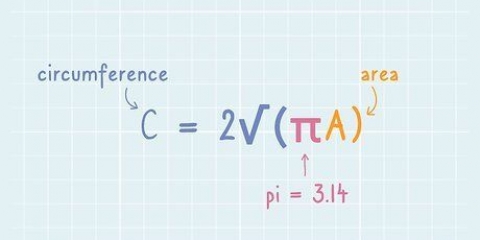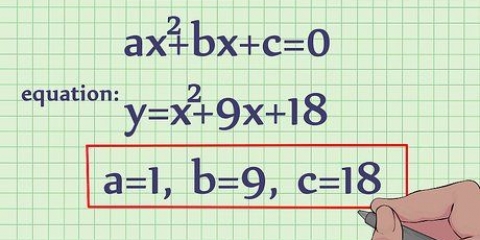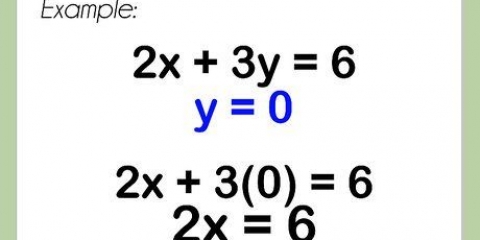Selfs die π-knoppie op `n sakrekenaar gebruik nie die presiese waarde van π nie, alhoewel dit akkuraat genoeg is. 
C is net `n korter manier om `omtrek` te skryf. 
Jy het dalk die linkerkant geskryf as π2r, wat ook korrek is. Mense hou daarvan om die getalle voor die simbole te plaas om die vergelyking makliker te lees, maar dit verander nie die resultaat van die vergelyking nie. In `n wiskundevergelyking kan jy altyd die linker- en regtersye met dieselfde hoeveelheid vermenigvuldig en steeds `n korrekte vergelyking kry. 
Byvoorbeeld, as die radius twee eenhede lank is, dan is 2πr = 2 x (3.14) x (2 eenhede) = 12.56 eenhede = die omtrek. In dieselfde voorbeeld, maar met die π-knoppie van `n sakrekenaar vir beter akkuraatheid, kry jy 2 x π x 2 eenhede = 12,56637... eenhede, maar tensy jou onderwyser anders opdrag gee, kan jy die getal afrond tot 12,57 eenhede. 

Ons gebruik d`, nie2r, want jou wiskunde probleem vertel jou wat d beteken. Dit is egter belangrik om hierdie stap te verstaan sodat jy nie deurmekaar raak as jou onderwyser of wiskunde boek 2r gebruik waar jy `n d sou verwag. 
Selfs die π-knoppie op `n sakrekenaar gebruik nie die presiese waarde van π nie, alhoewel dit baie akkuraat is. 

π x d = (C / d) x d πd = C 
Byvoorbeeld, as die deursnee ses is, kry jy (3,14) x (6) = 18,84. In dieselfde voorbeeld, maar met `n sakrekenaar se π-knoppie vir meer akkuraatheid, kry jy π x 6 = 18,84956... maar tensy anders vermeld, kan jy die getal afrond tot 18,85. 


A = r A / π = πr / π = r √(A/π) = √(r) = r r = √(A/π) 
C = 2πr C = 2π(√(A/π)) 
Die antwoord vir hierdie voorbeeld is 13.72937... maar tensy anders aangedui, kan jy die antwoord afrond tot 13.73. 


Maak seker dat jy die tou meer as een keer om dit draai. Jy moet eindig met `n enkele lus sodat daar geen deel van die sirkel is waar die tou dubbel toegedraai is nie. 

Vind die omtrek van 'n sirkel
Inhoud
Die omtrek van `n sirkel is die afstand om sy rand. As `n sirkel `n omtrek van 2 myl het, moet jy 2 myl om die sirkel loop voordat jy terugkeer na waar jy begin het. As jy egter aan `n meetkundige probleem werk, hoef jy nie uit jou stoel te klim nie. Lees die probleem aandagtig deur om uit te vind of die `radius` (r), `deursnee` (d) of `oppervlakte` (A) van die sirkel gegee is, en vind dan die deel van hierdie artikel wat bedoel is om jou te help met die taak. Daar is ook instruksies vir die vind van die omtrek van `n bestaande sirkelvormige voorwerp wat jy wil meet.
Trappe
Metode 1 van 4: Bepaal die omtrek deur die radius te gebruik

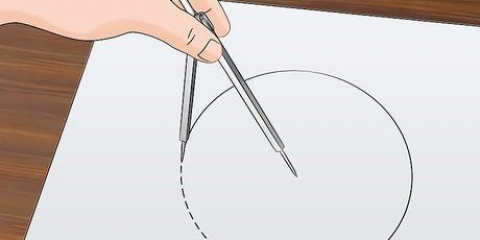
1. Teken `n `straal` op die sirkel. Trek `n lyn van die middel van die sirkel na enige posisie op die rand van die sirkel. Hierdie lyn is die `radius` van die sirkel, dikwels geskryf as `r` in wiskundige vergelykings en formules.
- `Opmerking: as die radius nie in die wiskundeprobleem gegee word nie, is dit dalk nie die korrekte instruksies nie. Kyk of dié oor die deursnee of oppervlak meer bruikbaar is vir die opdrag.

2. Trek `n `deursnee` oor die sirkel. Brei die lyn wat jy pas getrek het uit sodat dit die sirkelrand aan die ander kant bereik. Jy het sopas `n tweede straal geteken. Die twee bygevoegde radiusse het `n lengte van `2 x die radius`, geskryf as 2r. Die lengte van hierdie lyn is die `deursnee` van die sirkel, dikwels geskryf as d.

3. Verstaan π (`pi`). Die simbool π, ook geskryf as PI is nie `n towergetal wat toevallig in hierdie soort wiskundeprobleme gebruik word nie. Eintlik is die getal π oorspronklik `ontdek` deur sirkels te meet: as jy die omtrek van enige sirkel meet (byvoorbeeld met `n maatband), en dan deur die deursnee deel, eindig jy altyd met dieselfde getal. Hierdie getal is ongewoon omdat dit nie as `n eenvoudige breuk of desimale geskryf kan word nie. In plaas daarvan kan ons dit afrond tot `n getal soos 3,14, wat "goed genoeg" is.

4. Skryf die definisie van π as `n algebraprobleem neer. Soos hierbo verduidelik, beteken π net `die getal wat jy kry as jy die omtrek deur die deursnee deel`. In die vorm van `n wiskundige formule is dit: π = C / d. Aangesien ons weet dat die deursnee gelyk is aan 2 x die radius, kan ons dit ook skryf as π = C / 2r.

5. Verander hierdie probleem sodat jy hierdie probleem vir die omtrek C oplos. Ons wil weet wat die omtrek is (C in hierdie wiskundeprobleem). As jy beide kante vermenigvuldig met 2r jy kry π x 2r = (C / 2r) x 2r, en dit is dieselfde as 2πr = C.

6. Vervang die getalle om op te los vir C. Nou weet ons dit 2πr = C. Keer terug na die oorspronklike wiskundeprobleem om te sien wat r (die radius) is. Vervang dan π met 3.14, of gebruik die π-knoppie op jou sakrekenaar om `n meer akkurate antwoord te kry. Bereken 2πr met hierdie getalle. Die antwoord wat jy kry is die omtrek.
Metode 2 van 4: Bepaal die omtrek deur die deursnee te gebruik

1. Verstaan wat `n `deursnee` is. Plaas jou potlood op die rand van die sirkel. Trek `n lyn deur die middel van die sirkel en die rand aan die ander kant. Hierdie lyn (van rand tot rand en deur die middel) is die `deursnee` van die sirkel, dikwels geskryf as d in wiskunde probleme.
- Die lyn gaan deur die presiese middelpunt van die sirkel, nie net enige plek in die sirkel nie.
- Opmerking: As die stelling nie aandui hoe lank die deursnee is nie, gebruik `n ander metode.

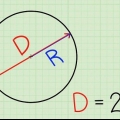
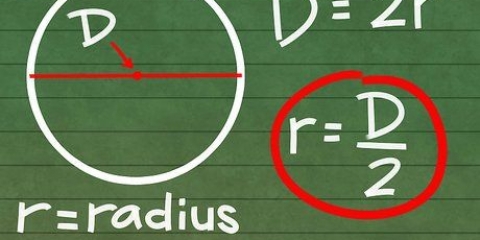
2. Leer wat d = 2r beteken. Die `radius` van die sirkel, ook geskryf as r, is die afstand van die middelpunt na die rand van die sirkel. Aangesien die deursnee deur die sirkel van rand tot rand, deur die middelpunt gaan, is die deursnee gelyk aan twee radiusse. `n Maklike manier om dit te skryf is d = 2r. Dit beteken dat jy d kan altyd vervang met 2r in `n wiskunde probleem, en omgekeerd.

3. Verstaan π (`pi`). Die simbool π, ook geskryf as PI is nie `n towergetal wat toevallig in hierdie soort wiskundeprobleme gebruik word nie. Eintlik is die getal π oorspronklik `ontdek` deur sirkels te meet: as jy die omtrek van enige sirkel meet (byvoorbeeld met `n maatband), en dan deur die deursnee deel, eindig jy altyd met dieselfde getal. Hierdie getal is ongewoon omdat dit nie as `n eenvoudige breuk of desimale geskryf kan word nie. In plaas daarvan kan ons dit afrond tot `n getal soos 3,14, wat "goed genoeg" is.

4. Skryf die definisie van π as `n algebraprobleem neer. Soos hierbo verduidelik, beteken π net `die getal wat jy kry as jy die omtrek deur die deursnee deel`. In die vorm van `n wiskundige formule is dit: π = omtrek / deursnee of π = C / d.

5. Verander hierdie probleem sodat jy hierdie probleem vir die omtrek C oplos. Ons wil weet wat die omtrek is, so ons moet C slegs aan die een kant kry. Doen dit deur elke kant van die vergelyking met d te vermenigvuldig:

6. Vervang die getalle en los C op. Keer terug na die oorspronklike probleem om te sien wat die deursnee is, en vervang die d in hierdie vergelyking met daardie getal. Vervang π met `n afronding soos 3.14, of gebruik die π-knoppie op jou sakrekenaar vir `n meer akkurate resultaat. Vermenigvuldig die waardes en d saam en jy kry die omtrek C.
Metode 3 van 4: Vind die omtrek deur die area te gebruik

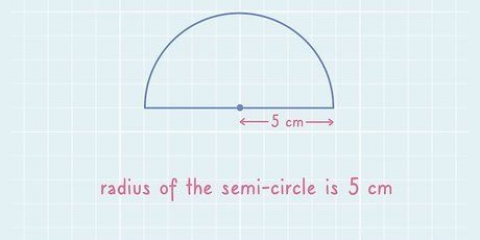
1. Verstaan hoe die oppervlakte van `n sirkel bereken word. Gewoonlik is die area (a) van `n sirkel wat nie direk gemeet is nie. In plaas daarvan, meet jy die radius (r) van die sirkel, en bereken dan die oppervlakte met die formule A = r. Die rede waarom hierdie formule sin maak, is `n bietjie moeilik om te verduidelik, maar jy kan meer leer deur hierdie skakel as jy belangstel en bereid is om tot die onderkant van een of ander swaarder algebra te kom.
- Opmerking: As die wiskundeprobleem nie die oppervlakte van die sirkel noem nie, moet jy dalk `n ander metode as hierdie artikel gebruik.

2. Leer `n formule om omtrek te bereken. Die omtrek (C) is die afstand om die sirkel. Jy bereken dit gewoonlik met die formule C=2πr, maar omdat ons nog nie weet wat die radius is nie (r), sal ons tyd moet spandeer om die waarde van uit te vind r voordat ons die vergelyking kan oplos.

3. Gebruik die oppervlakteformule om r aan die een kant te kry. Aangesien A = πr, kan ons hierdie formule herrangskik om eerder vir r op te los. As jy die stappe hieronder moeilik vind om te volg, wil jy dalk eers `n paar eenvoudiger algebra-probleme probeer of `n paar tegnieke oefen om algebra te verstaan.

4. Verander die omtrekformule deur wat jy gevind het. Elke keer as jy `n vergelyking soos r = √(A/π), kan jy die een kant van die vergelyking met die ander vervang?. Kom ons gebruik hierdie tegniek om die bogenoemde omtrekformule te kry, C=2πr, om te verander. Vir hierdie probleem ken ons nie die waarde van r nie, maar wel dié van A. Kom ons verander dit so om die probleem oplosbaar te maak:

5. Vervang die getalle om die omtrek te vind. Gebruik die area wat in die probleem gegee word om die omtrek van die omtrek te vind. Byvoorbeeld, as die area (a) van `n sirkel is 15 vierkante eenhede, vul dan in 2π(√(15/π)) in jou sakrekenaar. Moenie die hakies vergeet nie.
Metode 4 van 4: Bepaling van die omtrek van `n werklike sirkel

1. Gebruik hierdie metode om werklike sirkelvormige voorwerpe te meet. Jy kan die omtrek meet van sirkels wat jy in die regte wêreld vind, nie net in probleme nie. Probeer dit op `n fietswiel, `n pizza of `n muntstuk.

2. Neem `n stuk tou en `n liniaal. Die tou moet lank genoeg wees om die sirkel een keer te draai en buigsaam genoeg om styf te pas. Jy sal later iets nodig hê om die tou te meet, soos ’n liniaal of maatband. Die tou sal makliker wees om te meet as die liniaal langer is as die lengte van die tou.

3. Draai die tou een keer om die sirkel. Begin deur die een kant van die tou langs die rand van die sirkel te plaas. Draai die tou om die sirkel en trek dit styf. As jy `n muntstuk of ander dun voorwerp meet, kan jy dalk nie die tou styf om dit trek nie. Lê die sirkelvormige voorwerp plat en rangskik die tou om dit so styf as moontlik.

4. Merk of sny die tou. Vind die plek op die tou waar die lus eindig en raak aan die einde van die tou waarmee jy begin het. Merk hierdie plek met `n merker, of sny die tou op hierdie plek.

5. Maak die tou los en meet dit met `n liniaal. Neem die toegedraaide tou en meet dit met `n liniaal. As jy `n merker gebruik het, meet slegs van die einde van die tou tot by die merker. Dit is die deel van die tou wat om die sirkel draai, en aangesien die omtrek van `n sirkel net die afstand om die sirkel is, het jy die antwoord gevind! Die lengte van hierdie tou is gelyk aan die omtrek van die sirkel.
Wenke
- Jy kan die meervoud van radius as radiusse of as radiusse skryf.
Artikels oor die onderwerp "Vind die omtrek van 'n sirkel"
Оцените, пожалуйста статью
Soortgelyk
Gewilde