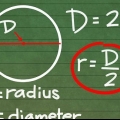
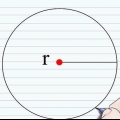
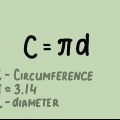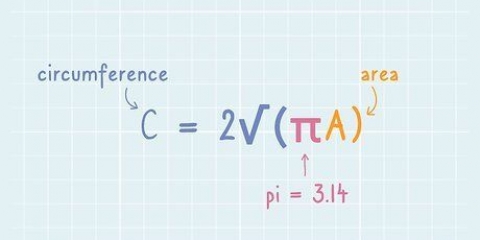Die radius (r) van `n sirkel is die afstand van een punt op die sirkel na die middel van die sirkel. Die deursnee (d) van `n sirkel is die afstand van een punt op die sirkel na `n ander punt direk oorkant die sirkel, wat deur die middel van die sirkel gaan. Die Griekse letter pi (π) staan vir die verhouding van die omtrek gedeel deur die deursnee en word voorgestel deur die getal 3.14159265..., `n irrasionale getal wat nie `n finale syfer of `n herkenbare patroon van herhalende syfers het nie. Hierdie getal word dikwels tot 3,14 afgerond vir standaardberekeninge. 
In die meeste wiskundeprobleme word die radius of deursnee gegee. 
Byvoorbeeld: Wat is die omtrek van `n sirkel met `n radius van 3 cm? Skryf die formule: C = 2πr Vul die veranderlikes in: C = 2π3 Vermenigvuldig: C = (2*3*π) = 6π = 18,84 cm Byvoorbeeld: Wat is die omtrek van `n sirkel met `n deursnee van 9 m? Skryf die formule neer: C = πd Vul die veranderlikes in: C = 9π Vermenigvuldig: C = (9*π) = 28,26 m 
Bepaal die omtrek van `n sirkel met `n deursnee van 5 m. C = πd = 5π = 15,7 m Bepaal die omtrek van `n sirkel met `n radius van 10 m. C = 2πr = C = 2π10 = 2 *10 *π = 62,8 m. 

Die radius (r) van `n sirkel is die afstand van een punt op die sirkel na die middel van die sirkel. Die deursnee (d) van `n sirkel is die afstand van een punt op die sirkel na `n ander punt direk oorkant die sirkel, wat deur die middel van die sirkel gaan. Die Griekse letter pi (π) staan vir die verhouding van die omtrek gedeel deur die deursnee en word voorgestel deur die getal 3.14159265..., `n irrasionale getal wat nie `n finale syfer of `n herkenbare patroon van herhalende syfers het nie. Hierdie getal word gewoonlik afgerond tot 3,14 vir basiese berekeninge. 
In die meeste wiskundeprobleme word die radius of deursnee gegee. 
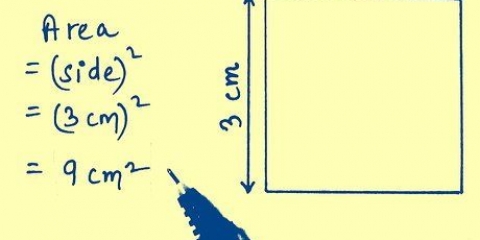
Byvoorbeeld: wat is die oppervlakte van `n sirkel met `n radius van 3 m? Skryf die formule: A = r. Vul die veranderlikes in: A = π3. Vierkant die radius: r = 3 = 9 Vermenigvuldig met pi: a = 9π = 28,26 m Byvoorbeeld: wat is die oppervlakte van `n sirkel met `n deursnee van 4 m? Skryf die formule: A = π(d/2). Vul die veranderlikes in: A = π(4/2). Deel die deursnee deur 2: d/2 = 4/2 = 2 Kwadra die resultaat: 2 = 4 Vermenigvuldig met pi: a = 4π = 12,56 m 
Vind die oppervlakte van `n sirkel met `n deursnee van 7 m. A = π(d/2) = π(7/2) = π(3.5) = 12.25 * π= 38.47 m. Vind die oppervlakte van `n sirkel met `n radius van 3 m. A = πr = π * 3 = 9 * π = 28,26 m 

Byvoorbeeld: bereken die omtrek van `n sirkel met `n radius van (x + 1). Skryf die formule: C = 2πr Vul die gegewe inligting in: C = 2π(x+1) 
Byvoorbeeld: bereken die omtrek van `n sirkel met `n radius van (x = 1). C = 2πr = 2π(x+1) = 2πx + 2π1 = 2πx +2π = 6.28x + 6.28 As die waarde van `x` later in die probleem gegee word, kan jy dit inprop en `n heelgetal kry. 
Vind die oppervlakte van `n sirkel met `n radius van 2x. A = πr = π(2x) = π4x = 12.56x Vind die oppervlakte van `n sirkel met `n deursnee van (x + 2). A = π(d/2) = π((x +2)/2) = ((x +2)/4)π
Berekening van die omtrek en oppervlakte van 'n sirkel
Inhoud
Die omtrek (C) van `n sirkel is sy omtrek, of die afstand daaromheen. Die oppervlakte (A) van `n sirkel is hoeveel spasie die sirkel in beslag neem of die oppervlakte wat deur die sirkel omring word. Beide oppervlakte en omtrek kan met eenvoudige formules bereken word vanaf die radius of deursnee van die sirkel en die waarde van pi.
Trappe
Deel 1 van 3: Berekening van die omtrek

1. Leer die formule vir die omtrek van `n sirkel. Daar is twee formules wat gebruik kan word om die omtrek van `n sirkel te bereken: C = 2πr of C = d, waar π die wiskundige konstante is en ongeveer gelyk aan 3.14,r is gelyk aan die radius en d gelyk aan die deursnee.
- Aangesien die radius van `n sirkel gelyk is aan twee keer sy deursnee, is hierdie vergelykings in wese dieselfde.
- Die eenhede vir die omtrek kan enige eenheid vir die lengtemaat wees: kilometer, meter, sentimeter, ens.

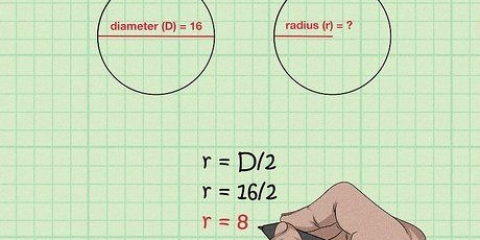
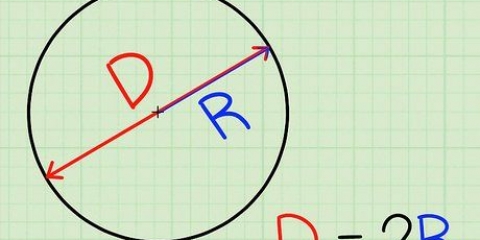
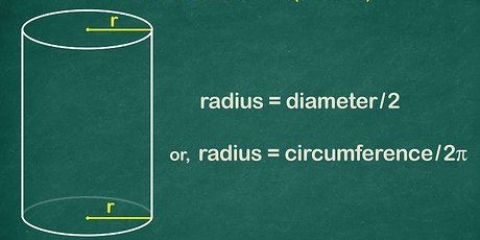
2. Verstaan die verskillende dele van die formule. Daar is drie komponente om die omtrek van `n sirkel te bepaal: radius, deursnee en π. Die radius en die deursnee hou verband: die radius is gelyk aan die helfte van die deursnee, terwyl die deursnee gelyk is aan twee keer die radius.

3. Meet die radius of deursnee van die sirkel. Plaas `n liniaal op die een rand van die sirkel, deur die middel en na die ander kant van die sirkel. Die afstand vanaf die middel van die sirkel is die radius, terwyl die afstand vanaf die ander kant van die sirkel die deursnee is.

4. Verwerk en los die veranderlikes op. Sodra jy die radius en/of deursnee van die sirkel bepaal het, kan jy hierdie veranderlikes in die toepaslike vergelyking plaas. As jy die balk het, gebruik C = 2πr, maar as jy die deursnee ken, gebruik dan C = d.

5. Oefen met `n paar voorbeelde. Noudat jy die formule geleer het, is dit tyd om te oefen met `n paar voorbeelde. Hoe meer probleme jy oplos, hoe makliker sal dit wees om dit in die toekoms op te los.
Deel 2 van 3: Berekening van oppervlakte

1. Leer die formule vir die oppervlakte van `n sirkel. Die oppervlakte van `n sirkel kan bereken word deur óf sy deursnee óf sy radius, met twee verskillende formules: A = r of A = π(d/2), waar π die wiskundige konstante is wat ongeveer gelyk is aan 3,14,r die radius en d die deursnee.
- Aangesien die radius van `n sirkel gelyk is aan die helfte van sy deursnee, is hierdie vergelykings in wese dieselfde.
- Die eenhede vir oppervlakte kan enige eenheid vir lengte kwadraat wees: km kwadraat (km), meter kwadraat (m), sentimeter kwadraat (cm), ens.

2. Verstaan die verskillende dele van die formule. Daar is drie komponente om die omtrek van `n sirkel te bepaal: radius, deursnee en π. Die radius en die deursnee hou verband met mekaar: die radius is gelyk aan die helfte van die deursnee, terwyl die deursnee gelyk is aan dubbel die radius.

3. Meet die radius of deursnee van die sirkel. Plaas die een kant van `n liniaal by `n punt op die sirkel, deur die middel en na die ander kant van die sirkel. Die afstand vanaf die middel van die sirkel is die radius, terwyl die afstand vanaf die ander punt op die sirkel die deursnee is.

4. Vul die veranderlikes in en los dit op. Sodra jy die radius en/of deursnee van die sirkel bepaal het, kan jy hierdie veranderlikes in die toepaslike vergelyking inprop. As jy die radius ken, gebruik A = r, maar as jy die deursnee ken, gebruik dan A = π(d/2).

5. Oefen met `n paar voorbeelde. Noudat jy die formule geleer het, is dit tyd om te oefen met `n paar voorbeelde. Hoe meer probleme jy oplos, hoe makliker sal dit wees om ander probleme op te los.
Deel 3 van 3: Berekening van die oppervlakte en omtrek met veranderlikes

1. Bepaal die radius of deursnee van die sirkel. Sommige probleme gee `n radius of deursnee met `n veranderlike, soos r = (x + 7) of d = (x + 3). In hierdie geval kan jy steeds die oppervlakte of die omtrek bepaal, maar jou finale antwoord sal ook daardie veranderlike bevat. Skryf die radius of deursnee neer soos in die stelling vermeld.
- Byvoorbeeld: bereken die omtrek van `n sirkel met `n radius van (x = 1).

2. Skryf die formule met die gegewe inligting. Of jy nou area of omtrek wil bereken, jy volg steeds die basiese stappe om in te vul wat jy weet. Skryf die formule vir oppervlakte of omtrek en vul dan die gegewe veranderlikes in.

3. Los die probleem op asof die veranderlike `n getal is. Op hierdie punt kan jy net die probleem oplos soos jy normaalweg sou doen, en die veranderlike behandel asof dit net nog `n getal is. Jy mag dalk die gebruik van distributiewe eiendom om die finale antwoord te vereenvoudig.

4. Oefen met `n paar voorbeelde. Noudat jy die formule geleer het, is dit tyd om te oefen met `n paar voorbeelde. Hoe meer probleme jy oplos, hoe makliker word dit om nuwes op te los.
Artikels oor die onderwerp "Berekening van die omtrek en oppervlakte van 'n sirkel"
Оцените, пожалуйста статью
Soortgelyk
Gewilde