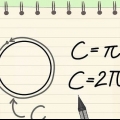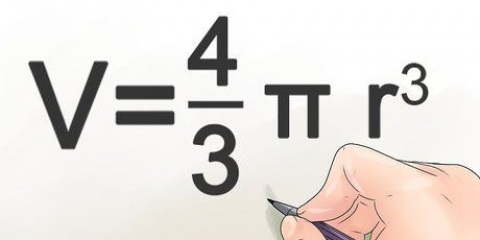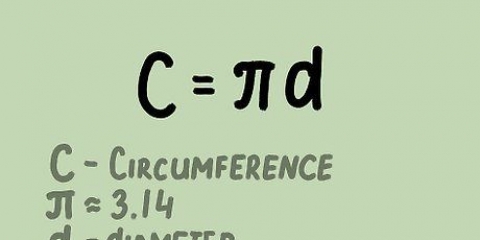Hoe om die radius van 'n sfeer te bereken

Inhoud

Trappe
Wenke

Die radius van `n sfeer (afgekort as die veranderlike r of R) is die afstand vanaf die presiese middelpunt van die sfeer na `n punt op die oppervlak van daardie sfeer. Net soos sirkels, die radius van `n sfeer is dikwels `n noodsaaklike eerste data vir die berekening van die deursnee, omtrek, oppervlakte en volume van `n sfeer. Jy kan egter ook agteruit werk vanaf die deursnee, omtrek, ens. om die radius van die sfeer te vind. Gebruik die formule wat geskik is vir die data wat jy het.

Trappe

Metode 1 van 3: Gebruik radiusformules

Prent getiteld Vind die radius van `n sfeer Stap 1

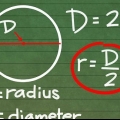
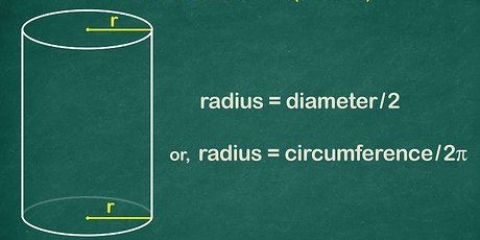
1. Bepaal die radius as jy die deursnee ken. Die radius is `n halwe deursnee, so jy gebruik die formule r = D/2. Dit is identies aan die metode vir die berekening van die radius van `n sirkel gegewe die deursnee.

As jy `n sfeer het met `n deursnee van 16 cm, bereken jy die radius met 16/2 = 8 cm. As die deursnee 42 is, dan is die radius 21.

Prent getiteld Vind die radius van `n sfeer Stap 2

2. Bepaal die radius as jy die omtrek ken. Gebruik die formule C/2π. Aangesien die omtrek gelyk is aan πD, wat op sy beurt gelyk is aan 2πr, bereken jy die radius deur die omtrek deur 2π te deel.

As jy `n sfeer het met `n omtrek van 20 m, sal jy die radius vind met 20/2π = 3,183 m.

Dieselfde formule kan gebruik word om tussen die radius en omtrek van `n sirkel om te skakel.

Prent getiteld Vind die radius van `n sfeer Stap 3

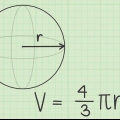
3. Bereken die radius as jy die volume van die sfeer ken. Gebruik die formule ((V/π)(3/4)). Die volume van `n sfeer word afgelei van die vergelyking V = (4/3)πr.Deur die vergelyking vir r op te los, kry jy ((V/π)(3/4)) = r, dus word dit duidelik dat die radius van `n sfeer gelyk is aan die volume gedeel deur π, maal 3/4, tot die 1/3 krag (of kubuswortel).

As jy `n bol met `n volume van 100 cm het, kry jy die radius soos volg:

((V/π)(3/4)) = r

((100/π)(3/4)) = r

((31.83)(3/4)) = r

(23.87) = r

2,88 = r

Prent getiteld Vind die radius van `n sfeer Stap 4

4. Bepaal die radius van die oppervlak. Gebruik die formule r = √(A/(4π)). Die oppervlakte van `n sfeer word bereken deur die vergelyking A = 4πr te gebruik. Die oplossing van die vergelyking vir r gee √(A/(4π)) = r, wat beteken dat die radius van `n sfeer gelyk is aan die vierkantswortel van sy oppervlakte gedeel deur 4π. Jy kan ook krag (A/(4π)) tot 1/2 vir dieselfde resultaat.

As jy `n sfeer met `n oppervlakte van 1200 cm het, bereken jy die radius soos volg:

√(A/(4π)) = r

√(1200/(4π)) = r

√(300/(π)) = r

√(95.49) = r

9,77 cm = r

Metode 2 van 3: Definieer sleutelterme

Prent getiteld Vind die radius van `n sfeer Stap 5

1. Ken die basiese afmetings van `n sfeer. Die radius (r) is die afstand vanaf die presiese middelpunt van die sfeer na enige punt op die sfeer se oppervlak. Oor die algemeen kan jy die radius van `n sfeer vind as jy sy deursnee, omtrek, volume of area ken.

Deursnee (D): die lengte van die lyn deur die middel van `n sfeer & ndash; dubbel die radius. Die deursnee is die lengte van `n lyn deur die middel van die sfeer: van een punt aan die buitekant van die sfeer na `n ooreenstemmende punt direk oorkant dit. Met ander woorde, die grootste moontlike afstand tussen twee punte op die sfeer.
Omtrek (C): die eendimensionele afstand om die sfeer op sy breedste punt. Met ander woorde, die omtrek van die sirkelvormige deursnee van `n sfeer waarvan die vlak deur die middel van die sfeer gaan.
Volume (V): die driedimensionele ruimte binne die sfeer. Dit is die "ruimte wat deur die sfeer ingeneem word".
Gebied (A): die tweedimensionele ruimte op die buitenste oppervlak van die sfeer. Die hoeveelheid plat spasie wat die buitekant van die sfeer bedek.
pi (π): `n konstante wat die verhouding van die omtrek van die sirkel tot die deursnee van die sirkel uitdruk. Die eerste 10 syfers van Pi is altyd 3,141592653, hoewel dit gewoonlik afgerond word tot 3.14.

Prent getiteld Vind die radius van `n sfeer Stap 6

2. Gebruik verskillende lesings om die radius te bepaal. Jy kan die deursnee, omtrek, volume en oppervlakte gebruik om die radius van `n sfeer te bereken. As jy die lengte van die radius ken, kan jy enige van hierdie getalle bereken. Dus, om die radius te vind, kan jy die formules vir die berekening van hierdie dele omkeer. Leer die formules wat radius behels om deursnee, omtrek, oppervlakte en volume te bereken.

D = 2r. Net soos sirkels is die deursnee van `n sfeer twee keer sy radius.

C = πD of 2πr. Net soos sirkels is die omtrek van `n sfeer gelyk aan π keer die deursnee. Aangesien die deursnee twee keer die radius is, kan ons ook sê dat die omtrek gelyk is aan twee keer die radius keer π.

V = (4/3)πr. Die volume van `n sfeer is sy radius na die kubus (r x r x r), keer π, keer 4/3.

A = 4πr. Die oppervlakte van `n sfeer is sy radius tot die tweede mag (r x r), keer π, keer 4. Aangesien die omtrek van `n sirkel gelyk is aan πr, kan daar ook gesê word dat die oppervlakte van `n sfeer gelyk is aan vier keer die oppervlakte van `n sirkel, soos gevorm deur sy omtrek.

Metode 3 van 3: Bepaal die radius as die afstand tussen twee punte

Prent getiteld Vind die radius van `n sfeer Stap 7

1. Bepaal die koördinate (x, y, z) van die middelpunt van die sfeer. Een manier om oor die radius van `n sfeer te dink, is as die afstand tussen die middel van die sfeer en enige punt op sy oppervlak. Aangesien dit waar is, kan jy die radius van die sfeer bepaal deur die koördinate van die middelpunt en `n punt op die oppervlak van die sfeer te gebruik, deur die afstand tussen die twee punte te bereken deur `n variant van die standaardafstandformule te gebruik. Om te begin, vind die koördinate van die middel van die sfeer. Let daarop dat `n sfeer driedimensioneel is, dit sal `n (x, y, z) punt wees in plaas van `n (x, y) punt.

Dit is makliker om te verstaan met `n voorbeeld. Veronderstel dat `n sfeer gegee word met as middelpunt(-1, 4, 12). In die volgende paar stappe gaan ons hierdie punt gebruik wanneer ons die radius bepaal.

Prent getiteld Vind die radius van `n sfeer Stap 8

2. Bepaal die koördinate van `n punt op die oppervlak van die sfeer. Dan moet jy die (x, y, z) koördinate van `n punt op die oppervlak van die sfeer bepaal. Dit is moontlik elk punt op die oppervlak van die sfeer. Omdat per definisie alle punte op die oppervlak van `n sfeer ewe ver van die middelpunt is, kan jy enige punt gebruik om die radius te bepaal.

In die konteks van ons voorbeeldopdrag stel ons dat die punt (3, 3, 0) op die oppervlak van die sfeer, gegee word. Deur die afstand tussen hierdie punt en die middelpunt te bereken, kan ons die radius vind.

Prent getiteld Vind die radius van `n sfeer Stap 9

3. Bepaal die radius met die formule d = √((x₂ - X₁) + (j₂ - y₁) + (z₂ - Z₁)). Noudat jy die middelpunt van die sfeer en `n punt op die oppervlak van die sfeer ken, kan jy die radius uitvind deur die afstand tussen hulle te bereken. Gebruik die driedimensionele afstandsformule d = √((x₂ - X₁) + (j₂ - y₁) + (z₂ - Z₁)), waar d die afstand is, (x₁,y₁,Z₁) verteenwoordig die koördinate van die middelpunt, en (x₂,y₂,Z₂) staan vir die koördinate van die punt op die oppervlak, om die afstand tussen beide punte te bepaal.

In ons voorbeeld vervang ons (4, -1, 12) vir (x₁,y₁,Z₁) en (3, 3, 0) vir (x₂,y₂,Z₂), waar ons dit soos volg oplos:

d = √((x₂ - X₁) + (j₂ - y₁) + (z₂ - Z₁))

d = √((3 - 4) + (3 - -1) + (0 - 12))

d = √((-1) + (4) + (-12))

d = √(1 + 16 + 144)

d = √(161)

d = 12,69. Dit is die radius van ons sfeer.

Prent getiteld Vind die radius van `n sfeer Stap 10

4. Weet dat in die algemeen, r = √((x₂ - X₁) + (j₂ - y₁) + (z₂ - Z₁)). In `n sfeer is elke punt op die oppervlak dieselfde afstand vanaf die middel van die sfeer. Kom ons neem die driedimensionele afstandformule hierbo en vervang die veranderlike "d" deur die veranderlike "r" van die radius, dan kry ons `n vergelyking wat ons in staat stel om die radius by enige gegewe middelpunt te vind (x₁,y₁,Z₁) en enige ooreenstemmende punt op die oppervlak (x₂,y₂,Z₂).

Deur beide kante van hierdie vergelyking te kwadraeer kry ons: r = (x₂ - X₁) + (j₂ - y₁) + (z₂ - Z₁). Let wel: Dit is in wese gelykstaande aan die standaardvergelyking vir `n sfeer (r = x + y + z), met die veronderstelling dat sy middelpunt gelyk is aan (0,0,0).

Wenke

Die volgorde van operasies maak saak. As jy nie seker is hoe die wiskundereëls werk nie, en jou sakrekenaar ondersteun hakies, maak seker dat jy dit gebruik.
Hierdie artikel is geskep omdat hierdie onderwerp hoog in aanvraag was. As jy egter vir die eerste keer probeer om ruimtelike meetkunde te verstaan, is dit waarskynlik beter om met die ander kant te begin: die berekening van die eienskappe van `n sfeer wanneer sy radius gegee word.
Pi of π is `n Griekse letter wat die verhouding van `n sirkel se deursnee tot sy omtrek aandui. Dit is `n irrasionale getal en kan nie as `n verhouding van reële getalle geskryf word nie. Daar is baie benaderings, en 333/106 gee pi tot vier desimale plekke. Vandag onthou die meeste mense die benadering 3.14 wat gewoonlik akkuraat genoeg is vir alledaagse doeleindes.