Berekening van die vertrouensinterval: 6 stappe (met prente)

Inhoud

Trappe
Wenke
Benodigdhede

Die vertrouensinterval is `n aanduiding van die akkuraatheid van jou lesings. Dit dui ook aan hoe stabiel jou skatting is; die mate waarin jou lesings ooreenstem met jou skatting as jy die eksperiment sou herhaal. Volg die stappe hieronder om die vertrouensinterval vir jou data te bereken.

Trappe

Prent getiteld Bereken vertrouensinterval Stap 1

1. Skryf die verskynsel neer wat jy wil toets. Gestel jy werk met die volgende situasie: Die gemiddelde gewig van `n manlike universiteitstudent A is 180 pond. Jy gaan nou toets hoe presies jy die gewig van die manstudente by universiteit A kan voorspel deur `n gegewe vertrouensinterval te gebruik.

Prent getiteld Bereken vertrouensinterval Stap 2

2. Neem `n steekproef uit jou gekose populasie. Dit is wat jy sal gebruik om die data in te samel om jou hipotese te toets. Gestel jy het 1000 ewekansige studente gekies.

Prent getiteld Bereken vertrouensinterval Stap 3

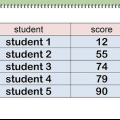
3. Bereken die steekproefgemiddelde en standaardafwyking. Kies `n steekproef (d.w.s. die steekproefgemiddelde en standaardafwyking) wat jy wil gebruik vir die skatting van die gekose populasieparameter. `n Bevolkingsparameter is `n sekere eienskap van die populasie. Hier is die steekproefgemiddelde en standaardafwyking:

Om die steekproefgemiddelde van die data te bereken, tel al die gewigte van die 1000 mans wat jy gekies het by en deel die resultaat deur 1000, die aantal mans. Die gemiddelde in hierdie voorbeeld is 180 pond.

Om die standaardafwyking te bereken, sal jy die gemiddelde van die data moet bereken. Nou is dit nodig om die variansie van die data te bereken, ook bekend as die gemiddelde van die kwadraat van die verskille van die gemiddelde. Sodra jy hierdie getal gevind het, trek sy vierkantswortel af. Gestel die standaardafwyking is 30 pond. (Soms word dit saam met `n taak gegee.)

Prent getiteld Bereken vertrouensinterval Stap 4

4. Kies die vertrouensvlak wat jy wil hê. Die mees algemene vertrouensvlakke is 90 persent, 95 persent en 99 persent. Dit is ook moontlik dat dit met `n taak gegee word. Gestel jy het 95% gekies.

Prent getiteld Bereken vertrouensinterval Stap 5

5. Bereken die foutmarge. U kan die foutmarge vind deur die volgende formule te gebruik: Z_a/2 * σ/√(n).Z_a/2 = vertroueskoëffisiënt, waar a = vertrouensvlak, σ = standaardafwyking en n = steekproefgrootte. Dit is nog `n manier om aan te dui dat jy die kritieke waarde met die standaardfout moet vermenigvuldig.Jy los die formule soos volg op deur dit te deel:

Bepaal die kritieke waarde, Z_a/2: Die vertrouensvlak is 95%. Skakel hierdie persentasie om na `n desimale, 0,95, en deel deur 2 om 0,475 te kry. Kyk dan in die volgende z tafel om die waarde te vind wat ooreenstem met 0,475. Die naaste waarde is 1.96, by die kruising van ry 1.9 en kolom 0.06.

Om die standaardfout te vind, neem die standaardafwyking 30 en deel dit deur die vierkantswortel van die steekproefgrootte (1000). Jy kry nou 30/31.6 = 0.95 pond.

Vermenigvuldig 1,96 met 0,95 (die kritieke waarde keer die standaardfout) en jy kry 1,86 of die foutmarge.

Prent getiteld Bereken vertrouensinterval Stap 6

6. Dui nou aan wat die vertrouensinterval is. Om dit te doen, neem die gemiddelde (180) en merk dit langs die ± en die foutmarge. Die antwoord is: 180 ± 1,86. Jy kan die boonste en onderste grense van die vertrouensinterval vind deur die foutmarge van die gemiddelde op te tel en af te trek. Dus, die ondergrens is 180 – 1,86 of 178,14, en die boonste grens is 180 + 1,86 of 181,86.

Jy kan ook die volgende handige formule gebruik om die vertrouensinterval te vind: x̅ ± Z_a/2 * σ/√(n). Hier stel x̅ die gemiddelde voor.

Wenke

Beide t-tellings en z-tellings kan met die hand, met `n sakrekenaar of met statistiese tabelle bereken word. Z-tellings kan ook met die Normale Verspreiding Sakrekenaar bepaal word, en t-tellings met die t Verspreiding Sakrekenaar. Aanlyn gereedskap is ook beskikbaar.
Die steekproefpopulasie moet normaal wees vir `n korrekte vertrouensinterval.
Die kritieke waarde wat gebruik word om die foutmarge te bereken is `n konstante uitgedruk as `n t-telling of as `n z-telling. T-tellings word gewoonlik verkies bo die populasie standaardafwyking is onbekend of wanneer `n klein steekproef gebruik word.
Daar is baie metodes, soos ewekansige steekproef, sistematiese steekproef en gestratifiseerde steekproef, wat jou toelaat om `n verteenwoordigende steekproef te neem om vir hipotesetoetsing te gebruik.
`n Vertrouensinterval sê niks oor die waarskynlikheid van `n bepaalde uitkoms nie. Byvoorbeeld, as jy 95% seker is dat jou populasiegemiddelde tussen 75 en 100 val, beteken die 95% vertrouensinterval nie dat daar `n 95 persent kans is dat die gemiddelde binne die berekende reeks val nie.