Berekening van die oppervlakte van 'n kubus
Inhoud
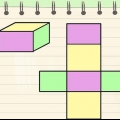
Die oppervlakte van `n voorwerp is die gekombineerde oppervlakte van al sy sye. Al ses sye van `n kubus is kongruent, dus om die oppervlakte van `n kubus te vind, moet jy net die oppervlakte van een kant van die kubus ken en dit dan met ses vermenigvuldig. As jy wil weet hoe om die oppervlakte van `n kubus te bereken, volg hierdie stappe.
Trappe
Metode 1 van 2: Wanneer die oppervlakte van een kant bekend is

1. Verstaan dat die oppervlakte van `n kubus die som is van die oppervlakte van sy ses sye. Aangesien alle kante van `n kubus kongruent is, kan ons net die oppervlakte van een kant vind en dit met ses vermenigvuldig om die totale oppervlakte te kry. Die area kan gevind word deur `n eenvoudige formule te gebruik: 6 x s, waar `s` `n rand van die kubus voorstel.

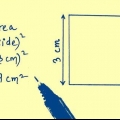
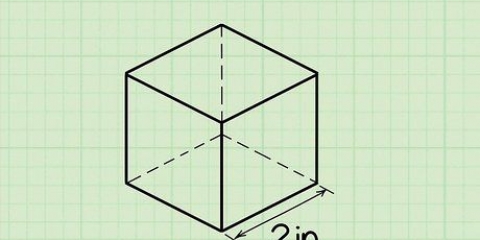
2. Vind die area van een gesig van die kubus. Om die oppervlakte van een vlak van die kubus te vind, moet jy `s` vind, wat die lengte van `n rand van `n kubus verteenwoordig, en dan s bereken. Dit beteken jy vermenigvuldig die lengte van die sy van die kubus met sy breedte om sy area te vind -- die lengte en breedte van die sy van `n kubus is dieselfde. As een kant van die kubus `s` 4 cm is, dan is die oppervlakte van die sy van die kubus (4 cm), of 16 cm. Moenie vergeet om jou antwoord in vierkante eenhede te stel nie.

3. Vermenigvuldig die oppervlakte van die kant van die kubus met ses. Noudat jy die oppervlakte van een vlak van die kubus gevind het, kan jy die oppervlakte van die kubus bepaal deur hierdie getal met ses te vermenigvuldig. 16cm x 6 = 96cm. Die oppervlak van die kubus is 96 cm.
Metode 2 van 2: Wanneer die volume bekend is

1. Vind die volume van die kubus. Kom ons sê die volume van die kubus is 125 cm.

2. Vind die derdemagswortel van die volume. Om die derdemagswortel van die volume te vind, soek `n getal wat tot die derde plek van die volume verhoog kan word, of gebruik `n sakrekenaar. Die getal sal nie altyd `n heelgetal wees nie. In hierdie geval is die getal 125 `n perfekte derdemag, en die vierkantswortel van die derdemag is vyf, want 5 x 5 x 5 x 5 x 5 = 125. So `s` (`n rand van die kubus), is vyf.

3. Pas hierdie antwoord toe op die formule vir die oppervlakte van `n kubus. Noudat jy die lengte van `n sy van `n kubus ken, voer dit in die formule in om die oppervlakte van `n kubus te vind: 6 x s. Aangesien die lengte van een rib gelyk is aan 5 cm, word die voltooide formule: 6 x (5 cm).

4. Los op. Dit is net `n bietjie wiskunde. 6 x (5 cm) = 6 x 25 cm = 150 cm.
Artikels oor die onderwerp "Berekening van die oppervlakte van 'n kubus"
Оцените, пожалуйста статью
Soortgelyk
Gewilde