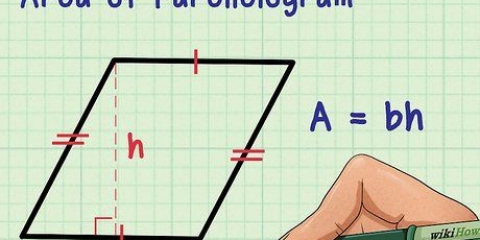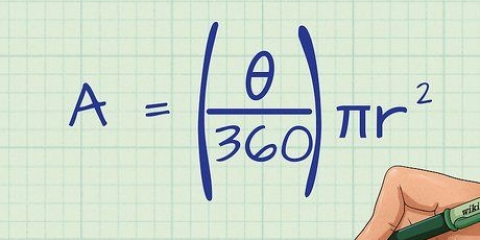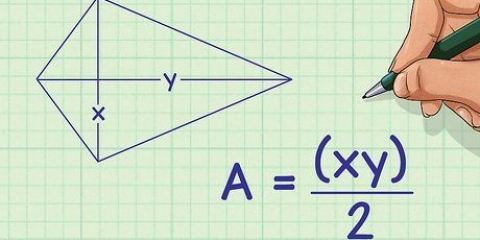Sien die apotem as die "x√3"-sy van `n 30-60-90 driehoek. Jy kan dit so sien omdat die seshoek uit ses gelyksydige driehoeke bestaan. Die apoteem sny een van hierdie driehoeke in die helfte en skep `n driehoek met hoeke van 30, 60 en 90 grade. Jy weet dat die sy oorkant die 60 grade hoek `n lengte van x√3 het, die sy oorkant die 30 grade hoek het `n lengte van x, en die sy oorkant die 90 grade hoek het `n lengte van 2x. As 10√3 staan vir "x√3," dan weet jy dat x = 10. Jy weet dat x die helfte van die lengte van die onderkant van die driehoek is. Verdubbel dit om die volle lengte te bepaal. Die onderkant van die driehoek is dus 20. Daar is ses van hierdie sye in die seshoek, so om die omtrek van die seshoek te vind vermenigvuldig ons 20 met 6 = 120. 
Oppervlakte = 1/2 x 120 x 10√3 Oppervlakte = 60 x 10√3 Oppervlakte = 600√3 


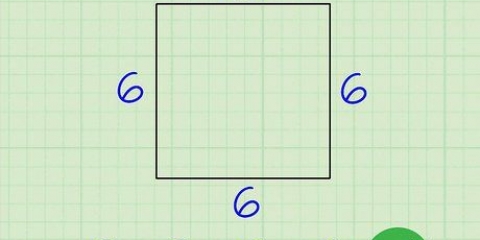
As jy `n vierkant het met sye van lengte 6, dan is die oppervlakte 6 x 6 = 36. 
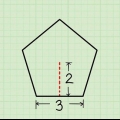
As die basis van `n reghoek 4 is en die hoogte is 3, dan is die oppervlakte 4 x 3 = 12. 
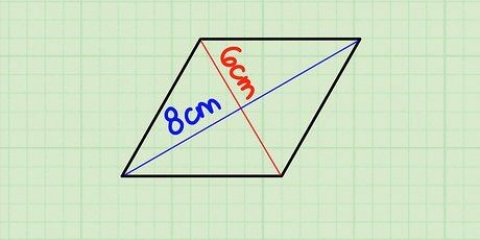
Gestel jy het `n trapesium waarvan die basisse lengtes 6 en 8 het en waarvan die hoogte 10 is. Dan is die area [(6 + 8) x 10]/2, wat vereenvoudig kan word na (14 x 10)/2 of 140/2, wat `n oppervlakte van 70 is. 





Bereken die oppervlakte van 'n veelhoek
Inhoud
Die berekening van die oppervlakte van `n veelhoek kan baie eenvoudig wees wanneer dit by `n gereelde driehoek kom. Maar dit word baie moeiliker as dit kom by `n onreëlmatige vorm met elf kante. As jy wil weet hoe om die oppervlakte van verskillende veelhoeke te bereken, volg hierdie stappe.
Trappe
Deel 1 van 3: Bereken die oppervlakte van veelhoeke deur die apotem te gebruik

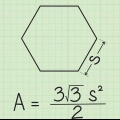
1. Skryf die formule om die oppervlakte van `n gereelde veelhoek te vind. Om die oppervlakte van `n gereelde veelhoek te vind, hoef u net die formule te volg: oppervlakte = 1/2 x omtrek x apotem. Dit beteken die volgende:
- Omtrek = die som van die lengtes van alle sye
- Apotem = die segment en ook die afstand vanaf die middel van die veelhoek na die middel van `n sy

2. Bepaal die apoteem van die veelhoek. As jy die apotem-metode gebruik, sal die apotem altyd `n gegewe wees. Gestel jy werk met `n seshoek waarvan die apoteem `n lengte van 10√3 het.

3. Bepaal die omtrek van die veelhoek. As die omtrek `n gegewe is, is jy amper klaar. Maar waarskynlik is net die apotem `n gegewe. As jy weet dat dit `n gereelde veelhoek is, kan jy die apotem gebruik om die omtrek daarvan te bepaal. Dis hoe jy dit doen:

4. Nou kan ons die apotem en omtrek in die formule plaas. Weereens: oppervlakte = 1/2 x omtrek x apotem, die omtrek is 120 en die apotem is 10√3. Dan lyk die formule soos volg:

5. Vereenvoudig jou antwoord. Miskien moet jy die resultaat in desimale skryf in plaas van `n radikaal. Gebruik jou sakrekenaar om die benaderde vierkantswortel van drie te vind en vermenigvuldig dit met 600. √3 x 600 = 1,039.2. Dit is die resultaat in desimale.
Deel 2 van 3: Vind die oppervlakte van `n gereelde veelhoek deur ander formules te gebruik

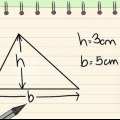
1. Bereken die oppervlakte van `n gelyke driehoek. As jy die oppervlakte van `n gereelde driehoek wil vind, kan jy hierdie formule gebruik: oppervlakte = 1/2 x basis x hoogte.
- As jy `n driehoek het met `n basis van 10 en `n hoogte van 8, dan is die oppervlakte = 1/2 x 8 x 10 = 40.

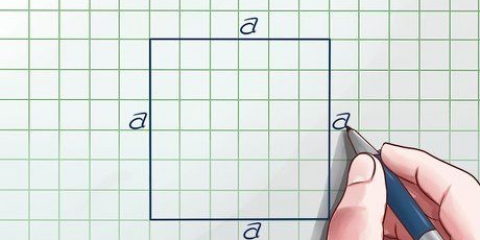
2. Bereken die oppervlakte van `n vierkant. Om die oppervlakte van `n vierkant te vind, hoef jy net een van sy sye met homself te vermenigvuldig, want die basis en hoogte is gelyk vir `n vierkant.

3. Bereken die oppervlakte van `n reghoek. Om die oppervlakte van `n reghoek te vind, hoef jy net die basis met sy hoogte te vermenigvuldig.

4.Bereken die oppervlakte van `n trapezium. Om die area van `n trapezium te vind, kan jy die volgende formule gebruik: oppervlakte = [(basis 1 + basis 2) x hoogte]/2.
Deel 3 van 3: Vind die oppervlakte van `n onreëlmatige veelhoek

1. Gebruik die koördinate van die nodusse om die oppervlakte te bereken. As jy die koördinate ken, kan jy die oppervlakte van `n onreëlmatige veelhoek bereken.

2. Skep `n volgorde. Lys die x- en y-koördinate van elke hoekpunt van die veelhoek, antikloksgewys. Herhaal die koördinate van die eerste punt onderaan die lys.

3. Vermenigvuldig die x-koördinaat van elke hoekpunt met die y-koördinaat van die volgende hoekpunt. Tel die resultate by. Die som van hierdie produkte is 82.

4. Vermenigvuldig die y-koördinaat van elke hoekpunt met die x-koördinaat van die volgende hoekpunt. Tel die resultate by. Die som van hierdie produkte is -38.

5. Trek die som van die produkte wat in stap 4 bereken is af van die som van die produkte wat in stap 3 bereken is. (82) - (-38) = 120.

6. Deel hierdie resultaat deur 2 om die oppervlakte van die veelhoek te vind. Oppervlakte = 120/2 = 60.
Wenke
- As jy die punte kloksgewys lys in plaas van antikloksgewys kry jy ook die area, maar negatief. Byvoorbeeld, jy kan dit as `n instrument gebruik om die sikliese volgorde van `n stel punte wat `n veelhoek vorm, te bepaal.
- Hierdie formule bereken oppervlakte met oriëntasie. As jy dit gebruik op `n vorm waar twee van die lyne sny soos in `n 8, kry jy die antikloksgewys area minus die kloksgewys area.
Artikels oor die onderwerp "Bereken die oppervlakte van 'n veelhoek"
Оцените, пожалуйста статью
Soortgelyk
Gewilde