Hoe om die oppervlakte van 'n gelykbenige driehoek (met prente) te bereken

Inhoud

Trappe
- Metode 1 van 2: Bepaal die oppervlakte deur die lengtes van elke kant te gebruik
- Metode 2 van 2: Gebruik trigonometrie
Wenke

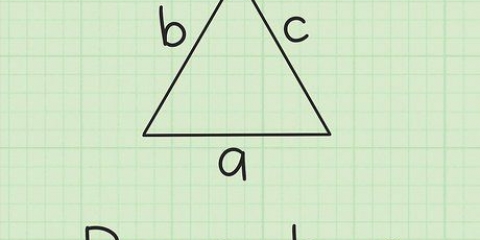
`n Gelykbenige driehoek is `n driehoek met twee sye van dieselfde lengte. Hierdie twee gelyke sye het altyd dieselfde hoek met die basis (die derde sy), en ontmoet direk bo die middel van die basis. Jy kan dit self toets met `n liniaal en twee potlode van gelyke lengte: as jy die driehoek in een rigting probeer kantel, sal die punte van die potlode nie ontmoet nie. Met hierdie spesiale eienskappe van die gelykbenige driehoek kan die oppervlakte met net `n paar stukkies data bereken word.

Trappe

Metode 1 van 2: Bepaal die oppervlakte deur die lengtes van elke kant te gebruik

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 1

1. Neem die oppervlakte van `n parallelogram. Vierkante en reghoeke is parallelogramme, soos enige viersydige vorm waar twee pare sye parallel aan mekaar is. Alle parallelogramme het `n eenvoudige oppervlakteformule: oppervlakte is gelyk aan basis vermenigvuldig met hoogte, of A = bh. As jy `n denkbeeldige parallelogram regop op `n horisontale oppervlak plaas, is die basis die lengte van die sy waarop die figuur is. Die hoogte is die afstand van die basis na die hoogste punt (soos jy sou verwag); dit wil sê die afstand van die basis na die teenoorgestelde kant. Meet altyd die hoogte teen `n regte hoek (90 grade) met die basis.

Vir vierkante en reghoeke is die hoogte gelyk aan die lengte van `n vertikale sy, aangesien hierdie sye reghoekig met die grond is.

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 2

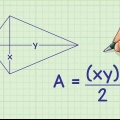
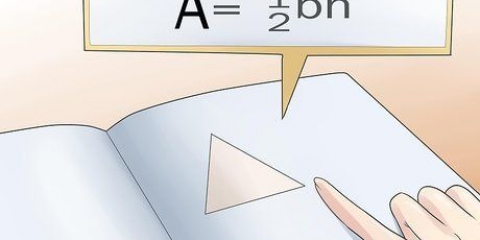
2. Vergelyk Driehoeke en Parallelogramme. Daar is `n eenvoudige verband tussen hierdie twee vorme. Deur `n parallelogram in die helfte langs die diagonaal te sny, verdeel dit in twee gelyke driehoeke. Net so kan jy twee identiese driehoeke saamvoeg om `n parallelogram te vorm. Dit beteken dat die oppervlakte van `n driehoek geskryf kan word as A = bh, presies die helfte van die grootte van `n ooreenstemmende parallelogram.

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 3

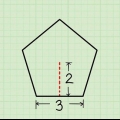
3. Vind die basis van die gelykbenige driehoek. Nou het jy die formule, maar wat presies is die `basis` en die `hoogte` van `n gelykbenige driehoek? Die basis is die maklike deel: neem net die derde, ongelyke sy van die gelykbenige driehoek.

Byvoorbeeld, as `n gelykbenige driehoek sye van 5 cm, 5 cm en 6 cm het, dan is die sy van 6 cm die basis.

As `n driehoek drie gelyke sye het (en dus gelyksydig is), dan kan jy enige sy as basis kies. `n Gelyksydige driehoek is `n spesiale soort gelykbenige driehoek, maar jy kan sy oppervlakte op dieselfde manier vind.

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 4

4. Trek `n lyn tussen die basis en die teenoorgestelde hoekpunt. Maak seker dat die lyn teen `n regte hoek aan die basis raak. Die lengte van hierdie lyn is die hoogte van die driehoek en word dus gemerk h. Sodra jy die waarde van h bereken, kan jy die area bepaal.

In `n gelykbenige driehoek raak hierdie lyn altyd die basis in sy presiese middelpunt.

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 5

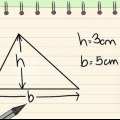
5. Kyk na die een helfte van die gelykbenige driehoek. Let daarop dat die hoogte die gelykbenige driehoek in twee identiese reghoekige driehoeke verdeel. Kyk na een van hulle en wys na die drie kante:

Een van die kort sye is gelyk aan die helfte van die basis:

\frac{b}{2}

${frac{b}{2}}$ .

Die ander kort kant is die hoogte h.

Die skuinssy (skuinssy) van die regte driehoek is een van die twee gelyke sye van die gelykbenige driehoek. Kom ons kry dit s te noem.

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 6

6.Gebruik die Pythagoras-stelling. As jy twee sye van `n reghoekige driehoek ken en die derde wil vind, kan jy die Pythagoras-stelling gebruik: (sy 1) + (sy 2) = (hypotenus) Vervang die veranderlikes wat ons in hierdie probleem gebruik en jy kry

(\frac{b}{2})^{2} + h^{2} = s^{2}

$({frac{b}{2}})^{2}+h^{2}=s^{2}$ .

Jy het waarskynlik die Pythagoras-stelling geleer as

a 2 + b^{2} = c^{2}

$a^{2}+b^{2}=c^{2}$ . Deur dit as `sye` en `hypotenusa` te skryf, verhoed jy om dit met die veranderlikes van die driehoek te verwar.

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 7

7. Los op vir h. Onthou dat jy die oppervlakteformule het b en h gebruik, maar wat jy nie weet wat die waarde daarvan is nie h weet nog nie. Herskryf die formule h om op te los:

(\frac{b}{2})^{2} + h^{2} = s^{2}

$({frac{b}{2}})^{2}+h^{2}=s^{2}$

h 2 = s^{2} - (\frac{b}{2})^{2}

$h^{2}=s^{2}-({frac{b}{2}})^{2}$

h = \sqrt{(} s^{2} - (\frac{b}{2})^{2})

$h={sqrt(}s^{2}-({frac{b}{2}})^{2})$ .

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 8

8. Vervang die waardes van jou driehoek met h Noudat jy hierdie formule ken, kan jy dit gebruik vir `n gelykbenige driehoek waarvan jy die sye ken. Voer net die lengte van die basis in vir b en die lengte van een van die gelyke sye vir s, en bereken daarna h.

Byvoorbeeld, jy het `n gelykbenige driehoek met sye 5 cm, 5 cm en 6 cm. b = 6 en s = 5.

Gebruik hierdie waardes in jou formule:

h = \sqrt{(} s^{2} - (\frac{b}{2})^{2})

$h={sqrt(}s^{2}-({frac{b}{2}})^{2})$

h = \sqrt{(} 5^{2} - (\frac{6}{2})^{2})

$h={sqrt(}5^{2}-({frac{6}{2}})^{2})$

h = \sqrt{(} 25 - 3^{2})

$h={sqrt(}25-3^{2})$

h = \sqrt{(} 25 - 9)

$h={sqrt(}25-9)$

h = \sqrt{(} 16)

$h={sqrt(}16)$

h = 4

$h=4$ cm.

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 9

9. Gebruik die basis- en hoogtewaardes in die oppervlakteformule. Nou het jy wat jy nodig het om die formule vanaf die begin van hierdie afdeling te gebruik: Oppervlakte = ½bh. Vervang die waardes vir b en h in hierdie formule en bereken die antwoord. Moenie vergeet om jou antwoord in vierkante eenhede te skryf nie.

Om voort te gaan met die voorbeeld: die 5-5-6 driehoek het `n basis van 6 cm en `n hoogte van 4 cm.

A = bh
A = ½(6cm)(4cm)
A = 12 cm.

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 10

10. Probeer `n moeiliker voorbeeld. Die meeste gelykbenige driehoeke is moeiliker om mee te werk as in die vorige voorbeeld. Hoogte bevat dikwels `n vierkantswortel wat nie tot `n heelgetal vereenvoudig kan word nie. As dit die geval is, laat die hoogte as die vierkantswortel in die eenvoudigste vorm te staan. Hier is `n voorbeeld:

Wat is die oppervlakte van `n driehoek met sye 8 cm, 8 cm en 4 cm?

Die ongelyke kant is 4 cm, en die basis b.

Die hoogte

h = \sqrt{8} 2 - (\frac{4}{2})^{2}

$h={sqrt{8^{2}-({frac{4}{2}})^{2}}}$

= \sqrt{64 - 4}

$={sqrt{64-4}}$

= \sqrt{60}

$={sqrt{60}}$

Vereenvoudig die vierkantswortel deur te faktoriseer:

h = \sqrt{60} = \sqrt{4 * 15} = \sqrt{4} \sqrt{15} = 2 \sqrt{15} .

$h={sqrt{60}}={sqrt{4*15}}={sqrt{4}}{sqrt{15}}=2{sqrt{15}}$

Oppervlakte

= \frac{1}{2} b h

$={frac{1}{2}}bh$

= \frac{1}{2} (4) (2 \sqrt{15})

$={frac{1}{2}}(4)(2{sqrt{15}})$

= 4 \sqrt{15}

$=4{sqrt{15}}$

Laat hierdie antwoord soos aangedui, of gebruik `n sakrekenaar vir `n desimale skatting (ongeveer 15.49 cm2).

Metode 2 van 2: Gebruik trigonometrie

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 11

1. Begin met `n kant en `n hoek. As jy vertroud is met trigonometrie, dan kan jy die oppervlakte van `n gelykbenige driehoek vind, selfs al is nie een van die lengtes van sy sye bekend nie. Hier is `n voorbeeldprobleem waar slegs die volgende bekend is:

Die lengte s van die twee gelyke sye is 10 cm.
Die hoek θ tussen die twee gelyke sye is 120 grade.

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 12

2. Verdeel die gelykbenige driehoek in twee reghoekige driehoeke. Trek `n lyn van die hoekpunt af tussen die twee gelyke sye, wat die basis teen `n regte hoek sny. Jy het nou twee gelyke reghoekige driehoeke.

Hierdie lyn verdeel θ perfek in die helfte. Elke reghoekige driehoek het `n hoek van ½θ, of in hierdie geval (½)(120) = 60 grade.

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 13

3. Gebruik trigonometrie om die waarde van te bepaal h. Noudat jy `n reghoekige driehoek het, kan jy die trigonometriese funksies (sinus, cosinus en tangens) toepas. In die voorbeeldprobleem weet jy wat die skuinssy is en jy wil die waarde van hê h weet, die kant langs die bekende hoek. Gebruik die feit dat cosinus = aangrensend / skuinssy aan h om op te los:

cos(θ/2) = h/s

cos(60º) = h / 10

h = 10cos(60º)

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 14

4. Bepaal die waarde van die oorblywende kant. Daar is `n nog onbekende sy van die regte driehoek, wat jy X kan noem. Los dit op met die definisie sinus = teenoorgestelde / skuinssy:

sin(θ/2) = x / s

sin(60º) = x / 10

x = 10sin(60º)

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 15

5. Gebruik die verhouding van x tot die basis van die gelykbenige driehoek. Jy kan nou `uitzoem` na die betrokke gelykbenige driehoek. Die basis b van daardie hoek is gelyk aan 2X, aangesien dit in twee segmente verdeel is, elk met `n lengte X.

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 16

6. Gebruik die waardes h en b in die oppervlakteformule vir die driehoek. Noudat jy die basis en hoogte ken, kan jy die standaardformule A = ½bh toepas:

a = \frac{1}{2} b h

$A={frac{1}{2}}bh$

= \frac{1}{2} (2 X) (10 c O s 60)

$={frac{1}{2}}(2x)(10cos60)$

= (10 s i n 60) (10 c O s 60)

$=(10sin60)(10cos60)$

= 100 s i n (60) c O s (60)

$=100sin(60)cos(60)$

Deur `n sakrekenaar te gebruik (gestel op grade), kry jy ongeveer 43,3 cm2 as `n antwoord. Alternatiewelik, gebruik die eienskappe van trigonometrie om hulle te vereenvoudig na A = 50sin(1200).

Prent getiteld Vind die oppervlakte van `n gelykbenige driehoek Stap 17

7. Herskryf dit as `n universele formule. Noudat jy weet hoe om dit reg te stel, kan jy die algemene formule toepas sonder om elke keer deur die hele proses te gaan. Hier is wat jy kry as jy hierdie proses herhaal, sonder om spesifieke waardes te gebruik (en om die trigonometrie-eienskappe te vereenvoudig):

a = \frac{1}{2} s^{2} s i n θ

$A={frac{1}{2}}s^{2}sintheta$

s is die lengte van een van die twee gelyke sye.

Θ is die hoek tussen die twee gelyke sye.

Wenke

As jy te doen het met `n gelykbenige reghoekige driehoek (twee gelyke sye en `n hoek van 90 grade), is dit baie makliker om die area te vind. As jy een van die kort sye as basis gebruik, is die ander kort kant die hoogte. Nou kan die formule A = ½ b * h vereenvoudig word na ½s, waar s die lengte van `n kort sy is.
Vierkantswortels het twee oplossings, een positief en een negatief, maar jy kan die negatiewe in meetkunde ignoreer. Byvoorbeeld, jy kan nie `n driehoek met `n `negatiewe hoogte` hê nie.
Sommige trigonometriese probleme gee jou ander inligting om mee te begin, soos die lengte van die basis en `n hoek (en die feit dat die driehoek gelykbenig is). Die basiese strategie bly dieselfde: verdeel die gelykbenige driehoek in reghoekige driehoeke en werk hulle uit vir hoogte deur gebruik te maak van trigonometriese funksies.