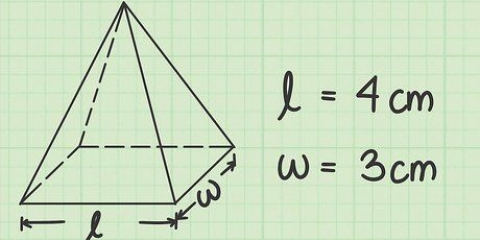Teken hierdie meting as a. Voorbeeld: a = 2 cm 
Let daarop dat hierdie stap die oppervlakte van `n gesig van die kubus bereken. Voorbeeld: a = 2 cm a = 2 x 2 = 4 cm 
Hierdie stap voltooi die berekening van die oppervlakte van die kubus. Voorbeeld: a = 4 cm Oppervlakte = 6 x a = 6 x 4 = 24 cm 

Meet die lengte van die basis om die lengte van die prisma te bepaal, en ken dit toe aan c. Voorbeeld: c = 5 cm Meet die breedte van die basis om die breedte van die prisma te bepaal, en noem dit a. Voorbeeld: a = 2 cm Meet die hoogte van die sy om die hoogte van die prisma te bepaal, en noem dit b. Voorbeeld: b = 3 cm 
Voorbeeld: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 cm 
Voorbeeld: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 cm 
Voorbeeld: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 cm 
Voorbeeld: Oppervlakte = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 cm. 

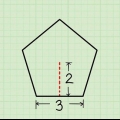
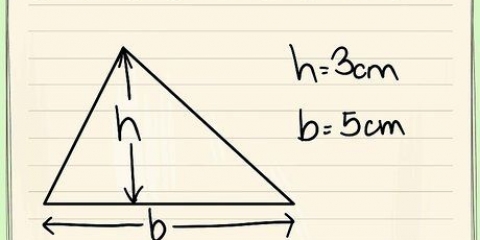
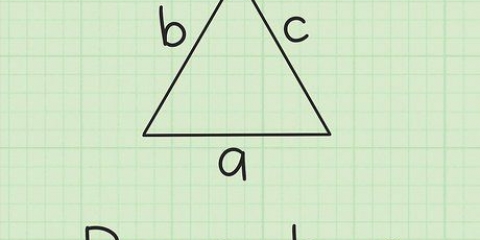
Die basis b, is gelyk aan die lengte van die onderkant van die driehoek. Voorbeeld: b = 4 cm Die hoogte h van die driehoekige basis is gelyk aan die afstand tussen die onderrand en die punt. Voorbeeld: h = 3 cm Die oppervlakte van een driehoek vermenigvuldig met 2 = 2(1/2)b*h = b*h = 4*3 =12 cm 
Voorbeeld: H = 5 cm Die drie sye verwys na die drie sye van die driehoekige basis. Voorbeeld: S1 = 2 cm, S2 = 4 cm, S3 = 6 cm 
Voorbeeld: P = S1 + S2 + S3 = 2 + 4 + 6 = 12 cm 
Voorbeeld: P x H = 12 x 5 = 60 cm 
Voorbeeld: 2A + PH = 12 + 60 = 72 cm. 

Voorbeeld: r = 3 cm 
Voorbeeld: r = r x r = 3 x 3 = 9 cm 
Voorbeeld: π*r = 3,14 x 9 = 28,26 cm 
Voorbeeld: 4π*r = 4 x 28,26 = 113,04 cm 

Voorbeeld: r = 3 cm Voorbeeld: h = 5 cm 
Voorbeeld: Oppervlakte van die basis = π*r = 3,14 x 3 x 3 = 28,26 cm Voorbeeld: 2π*r = 2 x 28,26 = 56,52 cm 
Voorbeeld: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 cm 
Voorbeeld: 2π*r + 2π*rh = 56.52 + 94.2 = 150.72 cm 

Voorbeeld: l = 3 cm Voorbeeld: s = 1 cm 
Voorbeeld: s = s x s = 1 x 1 = 1 cm 
Voorbeeld: 2 x s x l = 2 x 1 x 3 = 6 cm 
Voorbeeld: s + 2 ks = 1 + 6 = 7 cm 

Voorbeeld: r = 2 cm Voorbeeld: h = 4 cm 
Voorbeeld: l = √ (r + h) = √ (2 x 2 + 4 x 4) = √ (4 + 16) = √ (20) = 4,47 cm 
Voorbeeld: π*r = 3,14 x 2 x 2 = 12,56 cm 
Voorbeeld: π*rl = 3,14 x 2 x 4,47 = 28,07 cm 
Voorbeeld: π*r + π*rl = 12,56 + 28,07 = 40,63 cm
Bereken oppervlakte
Inhoud
Oppervlakte is die totale ruimte wat deur alle areas van `n voorwerp beset word. Dit is die som van alle areas van daardie voorwerp. Om die oppervlakte van `n driedimensionele vorm te bepaal is redelik maklik, solank jy die regte formule gebruik. Elke vorm het sy eie aparte formule, so jy sal eers moet kyk watter vorm dit is. Die berekening van die oppervlakteformule vir verskeie voorwerpe kan berekeninge in die toekoms makliker maak. Hier bespreek ons `n paar van die mees algemene vorms wat jy kan teëkom.
Trappe
Metode 1 van 7: Kubus

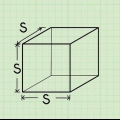
1. Definieer die formule vir die oppervlakte van `n kubus. `n Kubus het ses identiese vlakke. Aangesien beide die lengte en breedte van `n vierkant gelyk is, is die oppervlakte van `n vierkant a, waardeur a die lengte is een kant. Aangesien `n kubus ses gelyke vlakke het, kan jy sy oppervlakte bereken deur die oppervlakte van een van sy vlakke met ses te vermenigvuldig. Die formule vir die oppervlakte van `n kubus O is O = 6a, waardeur a die lengte is een kant.
- Die oppervlakte-eenhede is `n sekere lengte kwadraat: cm, dm, m, ens.

2. Meet die lengte van een kant. Per definisie moet elke sy of rand (rand) van `n kubus gelyk wees aan die ander, so jy hoef net een kant te meet. Meet die lengte van die sy met `n liniaal. Gee aandag aan die eenhede wat jy gebruik.

3. Vierkant jou meting vir a. Vierkant die meting om die lengte van die rib te bereken. Om `n waarde te kwadraat beteken om dit met homself te vermenigvuldig. As jy dit vir die eerste keer leer, kan dit nuttig wees om dit as te onthou NT= 6*a*a.

4. Vermenigvuldig hierdie produk met ses. Onthou dat `n kubus ses identiese vlakke het. Noudat jy die oppervlakte van een van die vlakke ken, vermenigvuldig dit met ses (as gevolg van al ses vlakke).
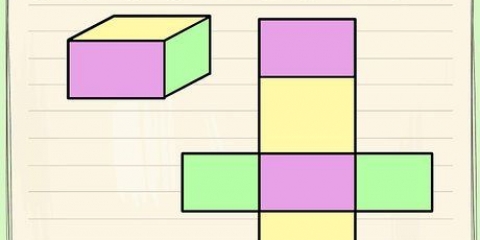
Metode 2 van 7: Reghoekige prisma

1. Definieer die formule vir die oppervlakte van `n reghoekige prisma. Soos `n kubus het `n reghoekige prisma ses vlakke, maar anders as `n kubus is daardie vlakke nie gelyk nie. In `n reghoekige prisma is slegs die teenoorgestelde vlakke gelyk aan mekaar. Daarom, wanneer die oppervlakte van `n reghoekige prisma bereken word, moet die verskillende lengtes van die ribbes in ag geneem word, soos in die formule SA = 2ab + 2bc + 2ac.
- Vir hierdie formule, a gelyk aan die breedte van die prisma, b gelyk aan die hoogte en c gelyk aan die lengte.
- As ons die formule van nader bekyk, sal jy sien dat ons eenvoudig al die areas van elke gesig van die voorwerp bymekaar tel.
- Die eenheid van oppervlakte sal `n sekere lengte kwadraat wees: cm, dm, m, ens.

2. Meet die lengte, hoogte en breedte van elke kant. Al drie lesings kan verskil, so elkeen moet afsonderlik gemeet word. Meet elke kant met `n liniaal en teken die waarde aan. Gebruik dieselfde eenhede vir elke meting.

3. Bereken die oppervlakte van een van die vlakke van die prisma, en vermenigvuldig dit met twee. Onthou dat daar ses vlakke in `n reghoekige prisma is, en die teenoorgestelde vlakke is gelyk aan mekaar. Vermenigvuldig die lengte en hoogte, of c en a, om die area van `n vliegtuig te vind. Neem hierdie meting en vermenigvuldig dit met twee om rekening te hou met die teenoorgestelde identiese vlak.

4. Vind die oppervlakte van die ander vlak van die prisma en vermenigvuldig dit met twee. Soos met die eerste stel gesigte, vermenigvuldig die breedte en hoogte, of a en b vir die bepaling van die area van `n ander vlak van die prisma. Vermenigvuldig hierdie meting met twee om rekening te hou met die teenoorgestelde identiese sye.

5. Bereken die oppervlakte van die punte van die prisma en vermenigvuldig dit met twee. Die ander twee vlakke van die prisma is die punte. Vermenigvuldig die lengte en breedte (c en b) om hul oppervlak te vind. Vermenigvuldig hierdie area met twee om beide kante in ag te neem.

6. Voeg die drie afsonderlike areas bymekaar. Aangesien die oppervlakte van die prisma die totale oppervlakte van alle vlakke van `n voorwerp is, is die laaste stap om alle individueel berekende oppervlaktes op te tel. Voeg die oppervlaktes van alle kante bymekaar om die totale oppervlakte te kry.
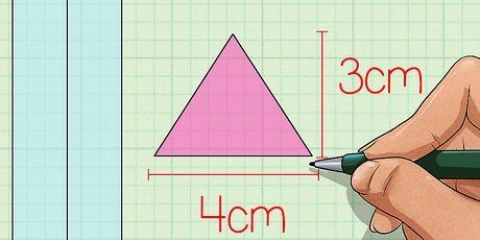
Metode 3 van 7: Driehoekige prisma

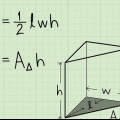
1. Definieer die oppervlakteformule vir `n driehoekige prisma. `n Driehoekige prisma het twee identiese driehoekige vlakke en drie reghoekige vlakke. Om die area te vind, moet jy die oppervlakte van al die gesigte bereken en hulle bymekaar tel. Die oppervlakte van `n driehoekige prisma is SA = 2A + PH, waar A die oppervlakte van die driehoekige basis is, P die omtrek van die driehoekige basis is, en h die hoogte van die prisma is.
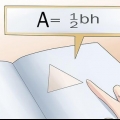
- Want hierdie formule hou dit in a die oppervlakte van `n driehoek en dus A = 1/2bh, waardeur b is die basis van die driehoek en h die hoogte.
- bl is die omtrek van die driehoek wat bereken word deur al drie kante van die driehoek by te tel.
- Die oppervlakte-eenhede is `n eenheid van lengte in die kwadraat: cm, dm, m, ens.

2. Bereken die oppervlakte van die driehoekige vlak en vermenigvuldig dit met twee. Die oppervlakte van `n driehoek is /2b*h waar b die basis van die driehoek is en h die hoogte is. Aangesien daar dus twee identiese driehoeke as vlakke is, vermenigvuldig ons die formule met twee. Dit maak die berekening vir beide vlakke maklik (b*h).

3. Meet elke sy van die driehoek en die hoogte van die prisma. Om die oppervlakteberekening te voltooi, moet jy die lengte van elke sy van die driehoek en die hoogte van die prisma ken. Die hoogte is die afstand tussen die twee driehoekige vlakke.

4. Vind die omtrek van die driehoek. Die omtrek van die driehoek kan bereken word deur al die gemete sye bymekaar te tel: S1 + S2 + S3.

5. Vermenigvuldig die omtrek van die basis met die hoogte van die prisma. Onthou dat die hoogte van die prisma die afstand tussen die twee driehoekige vlakke is. Met ander woorde, vermenigvuldig bl van huh.

6. Voeg die twee afsonderlike lesings saam. Jy moet die twee metings van die vorige twee stappe bymekaar voeg om die oppervlakte van die driehoekige prisma te kry.
Metode 4 van 7: Bol

1. Definieer die oppervlakteformule vir `n sfeer. `n Sfeer het `n geboë oppervlak, so die oppervlakte is `n waarde vermenigvuldig met die konstante, pi. Die oppervlakte van `n sfeer word met behulp van die vergelyking bereken NT = 4π*r.
- Vir hierdie formule, r gelyk aan die radius van die sfeer. Pi (of π) kan tot 3,14 afgerond word.
- Die eenhede van die area sal `n lengte-eenheid wees, kwadraat: cm, dm, m, ens.

2.Meet die radius van die gloeilamp. Die radius van die sfeer is die helfte van die deursnee, of die afstand vanaf die middel van die sfeer na die rand.

3. Vierkant die radius. Om `n getal te kwadraat, vermenigvuldig dit met homself. Vermenigvuldig die meting vir r met homself. Onthou dat hierdie formule herskryf kan word as SA = 4π*r*r.

4. Vermenigvuldig die kwadraatradius met `n afronding van PI. Pi is `n konstante wat die verhouding van `n sirkel se omtrek tot sy deursnee verteenwoordig. Dit is `n irrasionale getal met baie syfers na die desimale punt. Dit word dikwels tot 3,14 afgerond. Vermenigvuldig die kwadraatradius met π, of 3.14, vir die oppervlakte van `n sirkelvormige deursnit van die sfeer.

5. Vermenigvuldig hierdie produk met vier. Om die berekening te voltooi, vermenigvuldig dit met vier. Vind die oppervlakte van die sfeer deur die plat sirkelvormige area met vier te vermenigvuldig.
Metode 5 van 7: Silinder

1. Definieer die oppervlakteformule vir `n silinder. `n Silinder het twee sirkelvormige punte wat `n buisvormige oppervlak toemaak. Die formule vir die oppervlakte van `n silinder is NT = 2π*r + 2π*rh, waardeur r is gelyk aan die radius van die sirkelvormige basis en h gelyk aan die hoogte van die silinder. rond PI (of π) verminder tot 3,14.
- Die formule 2π*r bereken die oppervlakte van die twee sirkelvormige punte, terwyl 2πrh die oppervlakte van die kolom tussen die twee punte is.
- Die oppervlakte-eenhede is `n eenheid van lengte in die kwadraat: cm, dm, m, ens.

2. Meet die radius en hoogte van die silinder. Die radius van `n sirkel is die helfte van sy deursnee, of die afstand vanaf die middel van die sirkel tot by die rand. Die hoogte is die totale afstand van die silinder van die een kant na die ander. Teken hierdie mates met `n liniaal en skryf dit neer.

3. Vind die oppervlakte van die basis en vermenigvuldig dit met twee. Om die oppervlakte van die basis te vind, gebruik die oppervlakteformule of `n sirkel (π*r). Om die berekening te voltooi, vierkant die radius en vermenigvuldig dit met PI. Vermenigvuldig dan met twee as gevolg van die tweede identiese sirkel aan die ander kant van die silinder.

4. Bereken die oppervlak van die silinder self met 2π*rh. Dit is die formule vir die berekening van die oppervlakte van `n buis. Die buis is die spasie tussen die twee sirkelvormige punte van die silinder. Vermenigvuldig die radius met twee, PI en die hoogte.

5. Voeg die twee afsonderlike lesings saam. Voeg die oppervlakte van die twee sirkels by die oppervlakte van die spasie tussen die twee sirkels om die totale oppervlakte van die silinder te bereken. Let wel: Deur hierdie twee stukke by te voeg, herken jy die oorspronklike formule: NT =2π*r + 2π*rh.
Metode 6 van 7: Vierkantige Piramide

1. Definieer die oppervlakteformule vir `n vierkantige piramide. `n Vierkantige piramide het `n vierkantige basis en vier driehoekige sye. Soos genoem, is die oppervlakte van `n vierkant die lengte van een sy in die vierkant. Die oppervlakte van `n driehoek is 1/2sl (die sy van die driehoek maal die lengte of hoogte van die driehoek). Aangesien daar vier driehoeke is, bereken jy die totale oppervlakte deur dit met vier te vermenigvuldig. Deur al hierdie vlakke bymekaar te tel, kry die vergelyking van die oppervlakte vir `n vierkantige piramide: NT = s + 2k.
- In hierdie vergelyking, s die lengte van elke sy van die vierkantige basis en l die skuins hoogte van elke driehoekige sy.
- Die eenheid van oppervlakte is `n sekere lengte-eenheid in die kwadraat: cm, dm, m, ens.

2. Meet die skuins hoogte en basiskant. Die skuins hoogte l, is die hoogte van een van die driehoekige sye. Dit is die afstand van die basis tot by die punt van die piramide, gemeet langs `n plat kant. Die basiese kant s, is die lengte van een sy van die vierkantige basis. Aangesien die basis vierkantig is, is hierdie meting dieselfde vir alle kante. Gebruik `n liniaal vir elke meting.

3. Vind die oppervlakte van die vierkantige basis. Die oppervlakte van `n vierkantige basis kan bereken word deur die lengte van `n sy (s vermenigvuldig met homself).

4. Bereken die totale oppervlakte van die vier driehoekige vlakke. Die tweede deel van die vergelyking is die oppervlakte van die oorblywende vier driehoekige vlakke. Deur die formule 2ls te gebruik, vermenigvuldig ons s van l en twee. Vind die area van elke gesig.

5. Voeg die twee afsonderlike areas bymekaar. Voeg die totale oppervlakte van die vlakke by die oppervlakte van die basis om die totale oppervlakte te bereken.
Metode 7 van 7: Kegel

1. Definieer die oppervlakteformule vir `n keël. `n Kegel het `n sirkelvormige basis en `n ronde oppervlak wat op `n punt taps word. Om die area te vind, neem die area van die sirkelvormige basis en die area van die keël en voeg die twee bymekaar. Die formule vir die oppervlakte van `n keël is: SA = π*r + π*rl, waardeur r die radius is vanaf die sirkelvormige basis, l die skuins hoogte van die keël, en π is die konstante pi (3.14).
- Die eenheid van oppervlakte is `n sekere lengte-eenheid in die kwadraat: cm, dm, m, ens.

2. Meet die radius en hoogte van die keël. Die radius is die afstand vanaf die middel van die sirkelvormige basis na die rand van die basis. Hoogte is die afstand vanaf die middel van die basis tot by die punt van die keël, soos gemeet deur die middel van die keël.

3. Bereken die helling hoogte (l) van die keël. Aangesien die skuins hoogte die werklike skuinssy van `n driehoek is, moet jy die met behulp van Pythagoras se stelling vir die berekening daarvan. Gebruik die herrangskik vorm, l = √ (r + h), waardeur r die radius is en h die hoogte van die keël.

4. Vind die area van die sirkelvormige basis. Die oppervlakte van die basis word met die formule π*r bereken. Nadat jy die radius gemeet het, vier jy dit (sodat jy dit met homself vermenigvuldig) en dan vermenigvuldig jy daardie produk met pi.

5. Bereken die oppervlakte van die bokant van die keël. Gebruik die formule π*rl, waar r die radius is van die sirkel en l die helling soos hierbo bereken, om die oppervlakte van die bokant van die keël te bepaal.

6. Voeg die twee areas bymekaar om die totale oppervlakte van die keël te kry. Bereken die finale oppervlakte van die keël deur die oppervlakte van die sirkelvormige basis by te voeg wanneer die vorige stap bereken word.
Benodigdhede
- Heerser
- Pen of potlood
- Papier
Artikels oor die onderwerp "Bereken oppervlakte"
Оцените, пожалуйста статью
Soortgelyk
Gewilde