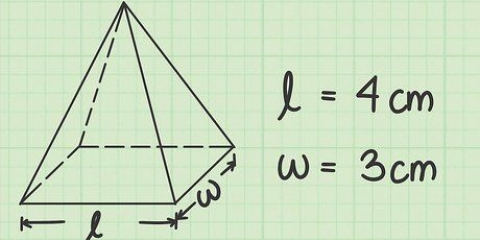Om s³ te vind, vermenigvuldig s drie keer met homself: s³ = s x s x s 
As jy nie 100% seker is of jou vorm `n kubus is nie, meet alle kante om te sien of hulle dieselfde is. Indien nie, sal jy die metode hieronder moet gebruik om die volume van `n balk te bereken. Let wel: In die voorbeeldfoto`s word die afmetings in duim (in) gegee, maar ons gebruik sentimeter (cm). 




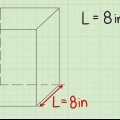
Voorbeeld: Die lengte van hierdie balk is 4 cm, dus l = 4 cm. Moenie te veel bekommer oor watter kant die lengte is nie, ens. Solank jy net drie verskillende kante meet, sal die resultaat dieselfde wees. 
Voorbeeld: Die breedte van hierdie balk is 3 cm, dus b = 3 cm. As jy die balk met `n liniaal of maatband meet, moenie vergeet om alles in dieselfde maateenheid neer te skryf nie. 
Voorbeeld: Die hoogte van hierdie staaf is 6 cm, dus h = 6 cm. 
In hierdie voorbeeld is l = 4, b = 3 en h = 6. Daarom is die uitkoms V = 4 x 3 x 6 = 72. 
Byvoorbeeld, as die balk se afmetings in meter was, sou jy l = 2 m, w = 4 m en h = 8 m kry. Die volume sal dan 2 m x 4 m x 8 m = 64 m³ wees. 

In die meeste gevalle is dit voldoende om pi tot 3,14 af te rond. Vra jou onderwyser wat hy/sy wil hê. Die formule om die volume van `n silinder te vind is eintlik baie soortgelyk aan dié van die volume van `n balk: jy vermenigvuldig die hoogte van die vorm met die oppervlakte van die basis. Vir `n balk is die oppervlakte van die basis l x b, vir `n silinder is dit π x r², die oppervlakte van `n sirkel met radius r. 

Nog `n opsie is om die omtrek van die sirkel (die afstand daaromheen) met `n stuk tou of `n maatband te meet. Plaas dan die resultaat in hierdie formule: C (omtrek) is 2 x π x r. Deel die omtrek deur 2 x π (6.28) en jy het die radius. Byvoorbeeld, as die omtrek wat jy gemeet het 8 cm is, dan is die radius 1,27 cm. As jy regtig `n presiese meting nodig het, kan jy enige metode gebruik om te sien of die resultate dieselfde is. Indien nie, kyk weer. Die omtrekmetode gee gewoonlik `n meer akkurate resultaat. 
As die radius 4 cm is, dan is die oppervlakte van die sirkel A = π x 4². 4² = 4 x 4, of 16. 16 xπ = 16 x 3,14 = 50,24 cm². As die deursnee van die basis bekend is, eerder as die radius, onthou dat d = 2 x r. Dan moet jy die deursnee deur twee deel om die radius te vind. 

V = π x 4² x 10 π x 4²= 50,24 50,24 x 10 = 502,4 V = 502,4 


Die formule vir reguit piramides, waar die toppunt direk bo die middel van die basis is, is dieselfde as vir skuins piramides, waar die toppunt nie in die middel is nie. 
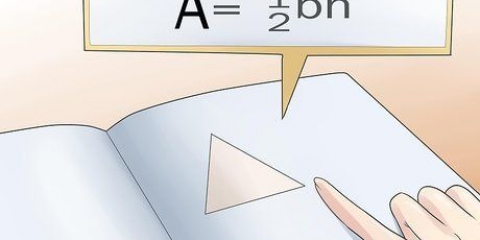
Die formule vir die oppervlakte van `n driehoek is A = 1/2 x b x h, waar b die basis is en h die hoogte is. Dit is moontlik om die oppervlakte van enige gereelde veelhoek te bereken deur die formule A = 1/2 xpxa te gebruik, waar A die oppervlakte is, p die omtrek is en a die apotem is, wat die afstand is vanaf die middel van die vorm na die middel van een van die kante. Jy kan dit ook vir jouself maklik maak en `n aanlyn gewone veelhoekrekenaar gebruik. 

As ons nog `n piramide gehad het met `n basis met `n oppervlakte van 26 en `n hoogte van 8, sou die resultaat gewees het: 1/3 x 26 x 8 = 69.33. 


Die deel π x r² verwys na die oppervlakte van die sirkel wat die basis van die keël vorm. Die formule vir die volume van die keël is dus 1/3 x b x h, net soos die formule vir die piramide in die metode hierbo! 
In hierdie voorbeeld is die radius 3 cm. As ons dit in die formule plaas, kry ons: A = π x 3². 3² = 3 x3, of 9, dus A = π x 9. A = 28.27cm². 


In ons voorbeeld is dit 141.35 x 1/3 = 47.12, die volume van die keël. Weereens: 1/3 x π x 3² x 5 = 47.12. 




Byvoorbeeld, as jy die bal meet en sien dat die omtrek 18 cm is, deel dit deur 6,28, jy weet dat die radius 2,87 cm is. Dit kan moeilik wees om `n sfeer te meet, daarom is dit die beste om dit drie keer te meet en dit te gemiddelde (tel die drie metings bymekaar en deel deur drie) om die meting so akkuraat as moontlik te kry. Byvoorbeeld, as jy drie keer gemeet het en die resultate was 18 cm, 17,75 cm en 18,2 cm, tel dit saam (18 + 17,5 + 18,2 = 53,95) en deel deur 3 (53,95/3 = 17,98). Jy gebruik hierdie gemiddelde wanneer jy die volume bereken. 


So in ons voorbeeld word dit 36 x 3,14 = 113,09. 
Bereken volume
Inhoud
Die volume van `n figuur is die driedimensionele ruimte wat die figuur beslaan. Jy kan volume voorstel as die hoeveelheid water (of lug, sand, ens.).) wat by die vorm sou pas as dit heeltemal vol was. Meeteenhede van volume wat algemeen gebruik word, is kubieke sentimeter en kubieke meter.Hierdie artikel sal jou leer hoe om die volume te bereken van ses verskillende driedimensionele vorms wat algemeen in wiskundetoetse voorkom, insluitend die kubus, sfeer en keël. Jy sal sien dat daar baie ooreenkomste is wat dit vir jou maklik sal maak om te onthou. Kyk of jy daardie pasmaats kan vind!
Trappe
Metode 1 van 6: Bereken die volume van `n kubus

1. Herken `n kubus. `n Kubus is `n driedimensionele vorm met ses identiese vierkantige vlakke.Met ander woorde, dit is `n boks met gelyke sye oral.
- `n Dobbelsteen is `n goeie voorbeeld van `n kubus wat jy dalk by die huis het. Suikerblokkies of kinderblokkies is dikwels ook blokkies.

2. Leer die formule om die volume van die kubus te bereken. Aangesien al die lengtes van die sye van die kubus dieselfde lengte is, is die formule vir die berekening van die volume van die kubus baie maklik. Die plek waar twee kante ontmoet word die rib genoem. Ons verkort volume tot "V". Die ribbes, of die lengte van die sy, noem ons hier "s". Die formule word dan V = s³

3. Vind die lengte van die een kant van die kubus. Afhangende van die opdrag kan hierdie inligting reeds daar wees, maar jy moet dit dalk ook self met `n liniaal meet. Onthou, aangesien dit `n kubus is, moet al die lengtes van die sye gelyk wees, so dit maak nie saak watter een jy meet nie.

4. Plaas die lengte van die sy in die formule V = s³ en bereken dit. Byvoorbeeld, as jy gemeet het dat die sylengte van jou kubus 5 cm is, sal jy die formule soos volg skryf: V = (5)³. 5 x 5 x 5 = 125 cm³, so dit is die volume van jou kubus!

5. Maak seker jy skryf jou antwoord in kubieke sentimeter. In die voorbeeld hierbo is die kubus in sentimeter gemeet, dus moet die antwoord in kubieke sentimeter gegee word. As die lengte van die sy van die kubus 3 meter was, dan sou die volume V = (3 m)³ = 27 m³ gewees het.
Metode 2 van 6: Bereken die volume van `n balk.

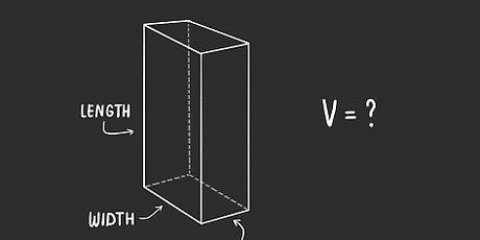
1. Herken `n balk. `n Balk is `n figuur wat uit ses reghoekige oppervlaktes bestaan. Dit is dus eintlik `n driedimensionele reghoek, `n soort boks.
- Eintlik is `n kubus net `n spesiale balk, waar alle kante gelyk is.

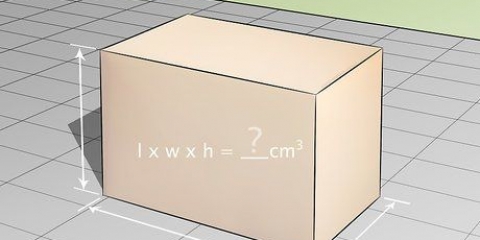
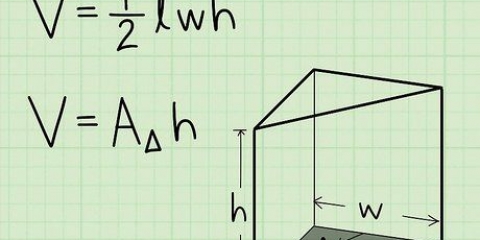
2. Leer die formule om die volume van `n balk te bereken. Die formule vir die volume van `n balk is V = lengte (l) x breedte (w) x hoogte (h), of V = l x b x h. Let wel: Die prente wat hierdie voorbeelde vergesel, wys "w" vir breedte.

3. Vind die lengte van die balk. Die lengte is die langste kant van die balk wat parallel is met die grond of oppervlak waarop dit rus. Die lengte is dalk reeds op die prentjie aangedui, of jy moet dit dalk met `n liniaal meet.

4. Vind die breedte van die balk. Die breedte van die balk kan gevind word deur die kort sy te meet wat parallel is met die grond of oppervlak waarop dit rus. Kontroleer eers weer of dit reeds op die prentjie aangedui is, en meet dit anders met jou liniaal.

5. Vind die hoogte van die balk. Hoogte is die afstand vanaf die grond of oppervlak waarop die balk rus tot by die bokant van die balk. Kyk of dit reeds in die prentjie aangedui is en meet dit anders met jou liniaal of maatband.

6. Tik die afmetings in die formule in en bereken dit. Onthou dat V = l x w x h.

7. Maak seker dat jy jou antwoord in kubieke sentimeter skryf. Die resultaat is dus 72 kubieke sentimeter, of 72 cm³.
Metode 3 van 6: Bereken die volume van `n silinder

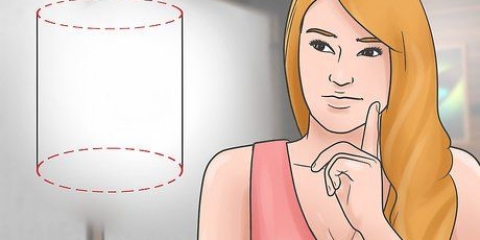
1. Leer hoe om `n silinder te identifiseer. `n Silinder is `n driedimensionele vorm met twee identiese ronde punte wat deur `n enkele geboë sy verbind is. Dit is eintlik `n reguit, ronde staaf.
- `n Blikkie is `n goeie voorbeeld van `n silinder, of `n AA-battery.

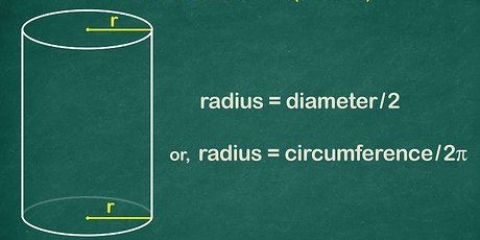
2. Memoriseer die formule vir die volume van `n silinder. Om die volume van `n silinder te bereken, moet jy sy hoogte en die radius van sy sirkelvormige basis ken.Die radius is die afstand vanaf die middel van die sirkel na die rand. Die formule is V =π x r² x h, waar V die volume is, r die radius is, h die hoogte is en π die konstante pi is.

3. Vind die radius van die basis. As dit reeds op die prentjie aangedui is, vul dit net in. As jy die deursnee in plaas van die radius gekry het, deel dit net deur 2 om die radius te vind (d = 2 x r).

4. Meet die vorm as die radius nie gegee word nie. Let daarop dat dit moeilik kan wees om die presiese radius van `n sirkel te meet. Een opsie is om die sirkel op sy breedste punt met jou liniaal van bo na onder te meet, en dit deur twee te deel.

5. Bereken die oppervlakte van die sirkel by die basis. Plaas die radius in die formule π x r². Vermenigvuldig die radius met homself en vermenigvuldig die resultaat met π. Byvoorbeeld:

6. Vind die hoogte van die silinder. Dit is bloot die afstand tussen die twee sirkelvormige basisse, of die afstand van die oppervlak waarop die silinder rus tot by die bokant van die silinder. Kyk of die lengte reeds in die prentjie aangedui is, of meet dit anders met jou liniaal of maatband.

7. Vermenigvuldig die oppervlakte van die basis met die hoogte van die silinder om die volume te vind. Plaas die waardes in die formule V =π x r² x h. In ons voorbeeld met `n radius van 4 cm en `n hoogte van 10 cm:

8. Onthou om jou antwoord in kubieke sentimeter te skryf. In hierdie voorbeeld is die silinder in sentimeter gemeet, dus moet die antwoord in kubieke sentimeter geskryf word: V = 502.4cm³. As die silinder in meter gemeet is, sou die volume in vierkante meter (m³) geskryf moes word.
Metode 4 van 6: Bereken die volume van `n gewone piramide

1. Weet wat `n gewone piramide is. `n Piramide is `n driedimensionele vorm met `n veelhoek aan die basis en sye wat na die bokant (die punt van die piramide) taps word.`n Gereelde piramide is `n piramide waarvan die basis `n reëlmatige veelhoek is, wat beteken dat alle sye en hoeke van hierdie veelhoek gelyk is.
- Gewoonlik word `n piramide uitgebeeld met `n vierkantige basis en sye wat in `n punt taps, maar die basis van `n piramide kan eintlik 5, 6 of 100 sye hê!
- `n Piramide met `n sirkel as sy basis word `n keël genoem, wat ons in die volgende metode sal bespreek.

2. Leer die formule vir die berekening van die volume van die gewone piramide. Die formule vir die volume van `n gewone piramide is V = 1/3 x b x h, waar b die oppervlakte van die basis is, en h die hoogte van die piramide is, of die vertikale afstand van die basis na bo.

3. Bereken die oppervlakte van die basis. Die formule hiervoor hang af van die aantal sye van die basis. In ons voorbeeld is die basis `n vierkant met sye van 6 cm. Onthou dat die formule vir die berekening van die oppervlakte van `n vierkant A = s² is. So met ons piramide is dit 6 x 6 = 36 cm².

4. Vind die hoogte van die piramide. In die meeste gevalle sal dit op die prentjie aangedui word. In ons voorbeeld is die hoogte van die piramide 10 cm.

5. Vermenigvuldig die oppervlakte van die basis van die piramide met die hoogte, en deel met 3 om die volume te vind. Onthou dat die formule V = 1/3 x b x h is. In ons voorbeeld het die piramide `n basis met `n oppervlakte van 36 en `n hoogte van 10, dus die volume is 36 x 10 x 1/3 = 120.

6. Onthou om die uitkoms in kubieke eenhede te skryf. Die afmetings van die piramide in die voorbeeld is in sentimeter gegee, dus moet die resultaat in kubieke sentimeter, 120 cm³ geskryf word. As die mates in meter gegee is, skryf die antwoord in kubieke meter (m³).
Metode 5 van 6: Bereken die volume van `n keël

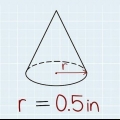
1. Leer wat die eienskappe van `n keël is. `n Kegel is `n driedimensionele vorm met `n sirkelvormige basis en `n enkele punt op die teenoorgestelde vlak. Nog `n manier om `n keël te sien, is dat dit `n spesiale soort piramide met `n sirkelvormige basis is.
- As die punt van die keël direk bo die middel van die basis is, word dit `n reguit keël genoem. As dit nie direk bo die middelpunt is nie, word dit `n skuins keël genoem. Gelukkig is die formule om volume te bereken dieselfde vir beide tipes keëls.

2. Ken die formule vir die berekening van die volume van die keël. Hierdie formule is V = 1/3 x π x r² x h, waar r die radius van die sirkel by die basis is, h die hoogte van die keël is en π die konstante pi is, wat tot 3,14 afgerond kan word.

3. Bereken die oppervlakte van die sirkelvormige basis van die keël. Om dit te doen moet jy die radius van die basis ken, wat op jou prentjie aangedui moet word. As jy die deursnee in plaas van die radius gekry het, deel net daardie getal deur 2, want die deursnee is 2 keer die radius (d = 2 x r). Plaas dan die radius in die formule A = π x r² om die oppervlakte te bereken.

4. Vind die hoogte van die keël. Dit is die vertikale afstand vanaf die basis van die keël na die bokant. In ons voorbeeld is die hoogte van die keël 5 cm.

5. Vermenigvuldig die hoogte van die keël met die oppervlakte van die basis. In ons voorbeeld is die oppervlakte van die basis 28,27 cm² en die hoogte is 5 cm, dus b x h = 28,27 x 5 = 141,35.

6. Vermenigvuldig nou hierdie resultaat met 1/3 (of deel deur 3) om die volume van die keël te kry. In die stap hierbo het ons eintlik die volume van `n silinder bereken, dit is `n keël waar die mure regop sou wees en in `n ander sirkel sou beland. Deur dit deur 3 te deel, gee jy die volume van die keël.

7. Onthou om die uitkoms in kubieke eenhede te skryf. Ons keël is in sentimeter gemeet, dus moet die volume in kubieke sentimeter uitgedruk word: 47,12 cm³.
Metode 6 van 6: Bereken die volume van `n sfeer

1. Herken `n sfeer. `n Bol is `n perfek ronde driedimensionele vorm, waarin elke punt op sy oppervlak ewe ver van die middelpunt af is. Met ander woorde, dit is `n bal.

2. Leer die formule vir die berekening van die volume van `n sfeer. Die formule is V = 4/3 x π x r³ (dws: "vier derdes pi keer kubieke r"), waar r die radius van die sfeer is, en π die konstante pi is (3.14).

3. Vind die radius van die sfeer. As die radius reeds in die prentjie gegee is, is dit maklik. Gegewe die deursnee, deel hierdie getal deur 2 om die radius te kry. Die radius van die sfeer in hierdie voorbeeld is 3 sentimeter.

4. Meet die sfeer as die radius nie gegee word nie. As jy `n bol (soos `n tennisbal) moet meet om die radius te vind, vind `n tou wat lank genoeg is om dit regdeur te draai. Draai dit dan om die voorwerp op die breedste punt en merk die punt waar die tou weer aansluit. Meet dan hierdie deel van die tou met `n liniaal om die omtrek van die sfeer te ken. Deel dit deur 2 x π, of 6.28, dan weet jy die radius.

5. Verhoog die radius tot die derde mag om r³ te vind. Verhoog tot die derde mag beteken eenvoudig om die getal drie keer met homself te vermenigvuldig, dus r³ = r x r x r. In ons voorbeeld word r=3 3 x 3 x 3 = 27.

6. Vermenigvuldig jou antwoord met 4/3. Jy kan dit met `n sakrekenaar doen, of sommer self doen en die breuk vereenvoudig. In ons voorbeeld is dit 27 x 4/3 = 180/3, of 36.

7. Vermenigvuldig die resultaat met π om die volume van die sfeer te vind. Die laaste stap in die berekening van die volume is om die resultaat tot dusver met π te vermenigvuldig. Rond π af tot twee desimale plekke, dit is genoeg vir die meeste wiskundeprobleme (tensy jou onderwyser anders sê), so vermenigvuldig dit met 3,14 en jy het jou antwoord.

8. Skryf jou antwoord in kubieke eenhede. In ons voorbeeld het ons in sentimeter gemeet, dus die antwoord is V = 113.09 cm³.
Artikels oor die onderwerp "Bereken volume"
Оцените, пожалуйста статью
Soortgelyk
Gewilde