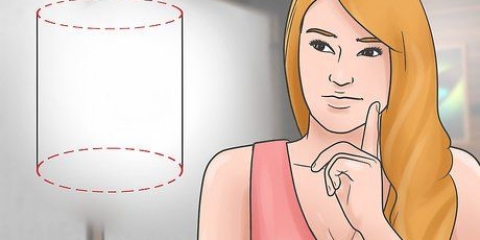
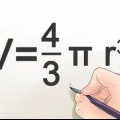Die radius, hoogte en apoteem (van die toppunt van die keël tot by `n punt op die omtrek) vorm `n reghoekige driehoek. Ons kan dus die Pythagoras-stelling hierop toepas. Gebruik altyd dieselfde eenheid vir die verskillende metings.
Bereken die volume van 'n keël
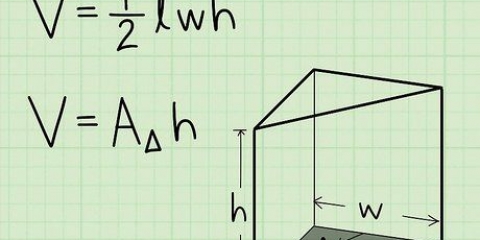
Jy kan maklik die volume van `n keël bereken as jy sy hoogte en radius ken. Die formule om die volume te bereken is dan soos volg: v = hπr/3. Hieronder verduidelik ons dit in maklike stappe.
Trappe
Metode 1 van 1: Bereken die volume van `n keël

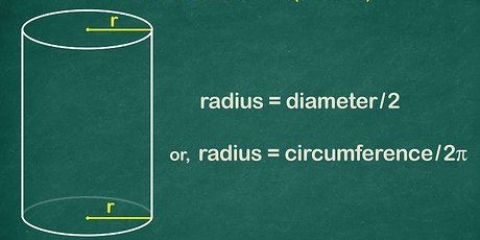
1. Bereken die radius. As jy reeds die radius ken, kan jy hierdie stap oorslaan en reguit na stap 2 gaan. As jy die deursnee van die sirkel ken, hoef jy dit net deur twee te deel om die radius te bereken. As jy die omtrek ken, bereken jy die radius deur die omtrek deur 2π te deel. En as jy ook nie die omtrek ken nie, hoef jy net `n liniaal te gryp en die deursnee te meet. Deel dan die gemete waarde deur twee en jy het die radius. Gestel die radius van die basis van hierdie keël is 0,5 cm.

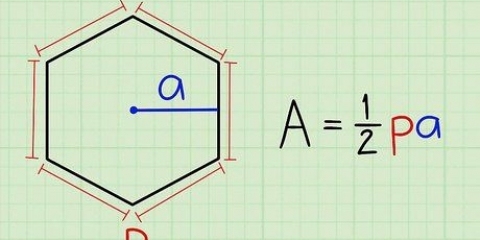
2. Gebruik die radius om die oppervlakte van die basis van die keël te bereken. Om dit te doen, gebruik eenvoudig die formule om die oppervlakte van `n sirkel te bereken: A = r. In die plek van "r" ons vul 5 in: A = π(0.5), of pi keer 0.5 kwadraat A = π(0.5) = 0.79 cm .

3. Meet die hoogte van die keël. As jy reeds die hoogte ken, moet jy dit net neerskryf. Gebruik `n liniaal as jy nog nie die hoogte ken nie. Gestel die hoogte van ons keël is 1,5 cm. Let wel: jy moet altyd seker maak dat die hoogte in dieselfde eenheid as die radius aangegee word; in hierdie geval sentimeter.

4. Vermenigvuldig die oppervlakte van die basis met die hoogte van die keël. Vermenigvuldig 0,79 cm by 1,5 cm. 0,79 cm x 1,5 cm = 1,19 cm.

5. Deel die resultaat deur drie. Deel 1,19 cm deur 3 om die volume van die keël te bereken. 1,19 cm/3 = 0,40 cm.
Wenke
- Maak seker dat jou afmetings presies is.
- Dit is hoe dit werk:
- Jy bereken eintlik die volume van `n keël deur eers voor te gee jy het met `n silinder te doen. In daardie geval neem jy die oppervlakte van die basis en vermenigvuldig dit met die hoogte van die silinder. En `n silinder pas altyd presies 3 keëls van dieselfde hoogte en met dieselfde basisoppervlak. dus as jy die volume van `n silinder deur drie deel kry jy die volume van drie keëls wat in die silinder pas.
Waarskuwings
- Moenie vergeet om die uitkoms deur 3 te deel nie.
Artikels oor die onderwerp "Bereken die volume van 'n keël"
Оцените, пожалуйста статью
Soortgelyk
Gewilde