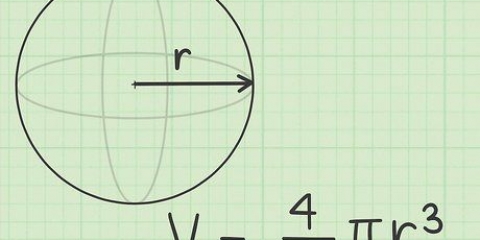
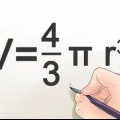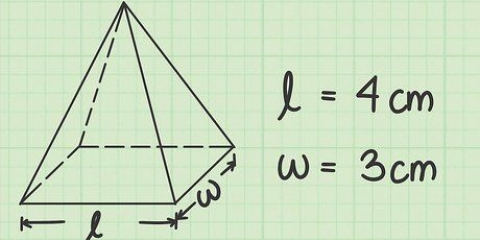bol: waar r die radius van die sfeer is.
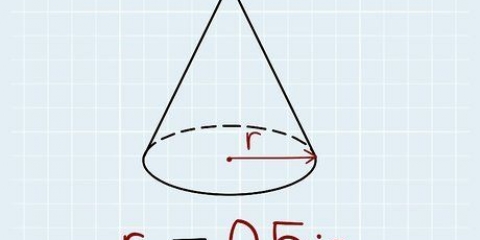
waar r die radius van die sfeer is. Keël: waar r die radius van die sirkelvormige basis is en h die hoogte van die keël is.
waar r die radius van die sirkelvormige basis is en h die hoogte van die keël is. Kubus:  waar s die lengte van `n sy is.
waar s die lengte van `n sy is. Reghoekige prisma:  waar l die lengte van `n sy van `n reghoekige vlak is, w die breedte van `n reghoekige vlak is en h die hoogte van die prisma is.
waar l die lengte van `n sy van `n reghoekige vlak is, w die breedte van `n reghoekige vlak is en h die hoogte van die prisma is. Silinder:  waar r die radius van die sirkelvormige basis is en h die hoogte van die keël is.
waar r die radius van die sirkelvormige basis is en h die hoogte van die keël is. Piramide:  waar B die oppervlakte van die basis van die piramide is en h die hoogte van die piramide is.
waar B die oppervlakte van die basis van die piramide is en h die hoogte van die piramide is. 
Die radius van `n sirkel is die helfte van sy deursnee. Meet die deursnee met `n liniaal deur die middel van die sirkel en lees die lesing. Bereken die radius deur die deursnee deur twee te deel. Om die radius van `n sfeer te bepaal verg `n bietjie meer moeite, maar kan op verskeie maniere gedoen word, soos in Hierdie artikel. Die lengte, breedte en hoogte van voorwerpe kan met `n liniaal gemeet word, van die een kant van `n voorwerp na die ander. 
Moenie vergeet om jou antwoord in kubieke eenhede te gee nie. Of jy nou metrieke of SI`s gebruik, die eenheid van volume is altyd kubieke. Voeg altyd eenhede aan die einde van jou berekening by. 

Wanneer die aanvanklike volume water gemeet word, kyk na die vloeistofvlak op ooghoogte en let op die lesing aan die onderkant van die meniskus. Die meniskus is die kurwe wat water maak wanneer dit met `n oppervlak in aanraking kom. 
As jy wel water gemors het terwyl jy die voorwerp in die beker geplaas het, probeer weer met `n groter maatbeker, of gebruik minder water. 
Gestel jy het byvoorbeeld met 35 ml water begin en met 65 ml water geëindig; die volume van jou voorwerp is dan 65 – 35 = 30 ml of 30 cm 


Bereken byvoorbeeld die digtheid  van `n stof met `n volume van 8 cm en `n massa van 24 g.
van `n stof met `n volume van 8 cm en `n massa van 24 g. 
Bereken volume en digtheid
Inhoud
Volume is die hoeveelheid spasie wat `n voorwerp beslaan terwyl digtheid die massa van die voorwerp per volume-eenheid is. Jy moet eers die volume van `n voorwerp ken voordat jy die digtheid daarvan kan bereken. Jy kan die volume vir gereelde voorwerpe bereken met `n eenvoudige formule, bepaal deur die vorm van die voorwerp. Algemeen gebruikte eenhede vir volume is die kubieke sentimeter (cm) en kubieke meter (m). Sodra jy die volume bereken het, dan word die digtheid met `n eenvoudige berekening bepaal. Algemeen gebruikte eenhede vir digtheid is gram per kubieke sentimeter (g/cm) of gram per milliliter (g/mL).
Trappe
Deel 1 van 3: Bereken die volume van `n gereelde voorwerp

1. Bepaal die vorm van die voorwerp. Deur die vorm van `n voorwerp te ken, kan jy die korrekte formule bepaal en die nodige berekeninge vir die volume doen.
- A sfeer is `n perfek ronde driedimensionele voorwerp, waar elke punt op sy oppervlak ewe ver van die middelpunt af is. Met ander woorde, `n sfeer is `n sferiese voorwerp.
- A keël is `n driedimensionele voorwerp met `n sirkelvormige basis en `n punt. Nog `n manier om hieraan te dink, is dat `n keël `n spesiale soort piramide met `n sirkelvormige basis is.
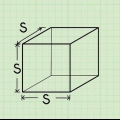
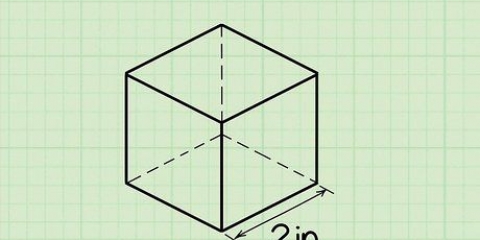
- A kubus is `n driedimensionele vorm met ses identiese vierkantige vlakke.
- A parallelepiped, ook `n reghoekige prisma genoem, lyk soos `n kubus aangesien dit `n driedimensionele vorm met ses sye is, maar in hierdie geval is die sye reghoekig in plaas van vierkantig.
- A silinder is `n driedimensionele vorm met twee identiese plat sirkels, en `n enkele geboë plat oppervlak wat beide sirkels verbind.
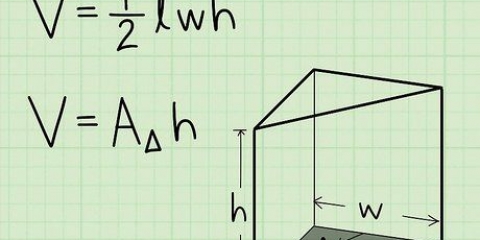
- A piramide is `n driedimensionele vorm met `n veelhoek as sy basis en skuins sye wat by `n punt (die punt van die piramide) ontmoet.`n Gereelde piramide is `n piramide met `n gereelde veelhoek as die basis van die piramide, wat beteken dat alle sye van die veelhoek ewe lank is, en alle hoeke ewe groot is.
- As jou voorwerp `n onreëlmatige vorm het, kan jy die verplasingsmetode gebruik om die volume daarvan te bepaal.

2. Kies die korrekte vergelyking vir die berekening van volume. Elke vorm het sy eie formule om te bereken hoeveel driedimensionele spasie dit opneem. Hieronder sal jy die formules vir die voorheen genoemde voorwerpe vind. Lees meer daaroor volume te bereken vir meer gedetailleerde voorbeelde en beelde van hierdie formules.
 waar r die radius van die sfeer is.
waar r die radius van die sfeer is. waar r die radius van die sirkelvormige basis is en h die hoogte van die keël is.
waar r die radius van die sirkelvormige basis is en h die hoogte van die keël is. waar s die lengte van `n sy is.
waar s die lengte van `n sy is. waar l die lengte van `n sy van `n reghoekige vlak is, w die breedte van `n reghoekige vlak is en h die hoogte van die prisma is.
waar l die lengte van `n sy van `n reghoekige vlak is, w die breedte van `n reghoekige vlak is en h die hoogte van die prisma is. waar r die radius van die sirkelvormige basis is en h die hoogte van die keël is.
waar r die radius van die sirkelvormige basis is en h die hoogte van die keël is. waar B die oppervlakte van die basis van die piramide is en h die hoogte van die piramide is.
waar B die oppervlakte van die basis van die piramide is en h die hoogte van die piramide is.
3. Maak die nodige metings. Die mates wat jy benodig word bepaal deur die vorm van die voorwerp. Vir die meeste voorwerpe het jy die hoogte nodig, maar die radius is genoeg as die vorm sirkelvormig is, of die lengte en breedte van voorwerpe met reghoekige vlakke.

4. Bereken die volume. Noudat jy die vorm bepaal het, weet watter formule om te gebruik en die nodige mates geneem het, kan jy die volume bereken. Voer jou lesings in en voer die nodige berekeninge uit. Die finale produk is die volume van jou voorwerp.
Deel 2 van 3: Bereken die volume van `n onreëlmatige voorwerp

1. Bereken die volume van die voorwerp deur verplasing te gebruik. Dit kan moeilik wees om die afmetings van onreëlmatige gevormde voorwerpe te bepaal, wat dan tot verkeerde metings en volumeberekeninge sal lei. Deur te meet hoeveel water deur `n voorwerp verplaas word, kan jy sy volume sonder komplekse formules bereken.
- Hierdie metode kan ook gebruik word om die volume van `n gereelde vorm te bereken.

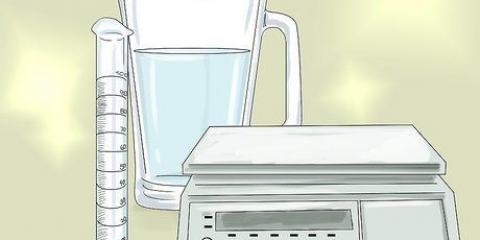
2. Vul `n gegradueerde silinder met water. `n Gegradueerde silinder is `n laboratoriuminstrument met merke aan die buitekant en laat jou toe om die volume van `n sekere hoeveelheid vloeistof te meet. Maak seker dat die gegradueerde silinder groot genoeg is om die voorwerp te hou. Vul dit met genoeg water sodat die voorwerp heeltemal onder die water is, maar die water nie oor die rand mors nie. Let op die aanvanklike vlak van die water.

3. Plaas die voorwerp rustig in die beker. Wees versigtig om nie die voorwerp in die water te laat val nie, anders kan water oor die rand vloei en die lesing sal verkeerd wees. Maak seker dat die voorwerp heeltemal onder water is. Let op die nuwe watervlak van die koppie, weer op ooghoogte, let noukeurig op die meniskus.

4. Trek die nuwe watervlak van die aanvanklike vlak af. Die hoeveelheid water wat deur die voorwerp verplaas word, is gelyk aan die voorwerp se volume gemeet in kubieke sentimeter. Vloeistowwe word gewoonlik in milliliter gemeet, en een milliliter is gelyk aan een kubieke sentimeter.
Deel 3 van 3: Berekening van digtheid

1. Bepaal die massa van die voorwerp. Die hoeveelheid materie in `n voorwerp is die massa van daardie voorwerp. Dit kan direk gemeet word deur die voorwerp op `n skaal te plaas met die eenheid in gram.
- Hou `n akkurate skaal byderhand en plaas die voorwerp daarop. Teken die massa daarvan in jou notaboek aan.
- Jy kan ook massa met `n balans meet. Met die voorwerp aan die een kant, plaas gewigte van bekende massa aan die ander kant van die weegskaal totdat hulle in ewewig is met die voorwerp. Die massa van jou voorwerp is gelyk aan die totale massa van die gewigte.
- Dit is belangrik om seker te maak dat jou item droog is voordat jy dit weeg. Sodoende is jy verseker dat die meetresultaat nie minder akkuraat is as gevolg van die geabsorbeerde water nie.

2. Bereken die volume van jou voorwerp. As jou voorwerp `n gereelde vorm het, bereken die volume deur een van die metodes wat voorheen aangedui is, te gebruik. As die vorm onreëlmatig is, bereken die volume deur die verplasingsmetode te gebruik soos hierbo verduidelik.

3. Bereken die digtheid. Digtheid word gedefinieer as die massa gedeel deur die volume. Ten slotte, om die digtheid te bepaal, deel die geweegde massa deur die gemete volume. Die resultaat is die digtheid van die metaal uitgedruk in g/cm.
 van `n stof met `n volume van 8 cm en `n massa van 24 g.
van `n stof met `n volume van 8 cm en `n massa van 24 g.
Wenke
- Jy kan jou volume berekeninge toets deur die resultaat van die verplasingsmetode en die berekeninge te vergelyk.
- Voorwerpe is dikwels `n samestelling van verskeie meetkundige voorwerpe, so jy kan hulle in kleiner basiese groepe verdeel om die volume van elkeen te bepaal, en dan almal bymekaar tel om die voorwerp se volume te bepaal.
Waarskuwings
- Maak seker dat jy alle metings in metrieke of SI-eenhede het voordat jy met jou berekeninge voortgaan.
Artikels oor die onderwerp "Bereken volume en digtheid"
Оцените, пожалуйста статью
Gewilde