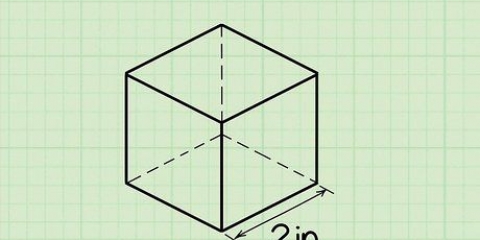
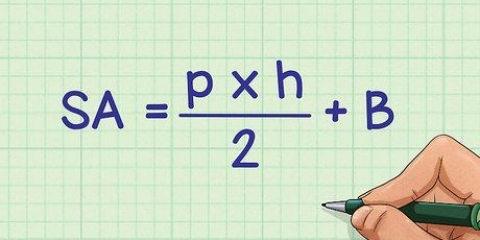In die voorbeeld is die sye van die basis van die piramide almal 5 cm, en jy bereken die oppervlakte van die basis soos volg: 
Onthou dat tweedimensionele oppervlaktes in vierkante uitgedruk word – vierkante sentimeter, meter, kilometer, ens. 
In die voorbeeld neem ons aan dat die piramide `n hoogte van 9 cm het. In hierdie geval, vermenigvuldig die oppervlakte van die basis met hierdie waarde, soos volg: 
Onthou dat volumes in kubieke eenhede uitgedruk word. In hierdie geval, omdat alle lineêre metings sentimeter is, word die volume in kubieke sentimeter aangedui. 
In die voorbeeld, deel 225 cm by 3 en die antwoord is 75 cm vir die volume. 


Hierdie vervanging lyk soos volg: 


 .....(oorspronklike vergelyking)
.....(oorspronklike vergelyking) .....(vierkant albei kante)
.....(vierkant albei kante) .....(tik waardes in)
.....(tik waardes in) .....(vereenvoudig breuk)
.....(vereenvoudig breuk) .....(vereenvoudig vierkant)
.....(vereenvoudig vierkant) .....(trek af)
.....(trek af) .....(vereenvoudig wortel)
.....(vereenvoudig wortel)
Uit die berekeninge lei ons af dat die hoogte van die piramide 12 cm is. Gebruik dit saam met die 10 cm-kant van die basis om die volume van die piramide te bereken: 









 ..........(aangepaste vergelyking)
..........(aangepaste vergelyking) ..........(vervang h aan beide kante)
..........(vervang h aan beide kante) ..........(trek die vierkantswortel van beide kante af)
..........(trek die vierkantswortel van beide kante af) ..........(vul die nommers in)
..........(vul die nommers in) ..........(vereenvoudig die vierkante)
..........(vereenvoudig die vierkante) ..........(trek waardes af)
..........(trek waardes af) ..........(vereenvoudig die vierkantswortel)
..........(vereenvoudig die vierkantswortel)Verdubbel hierdie waarde om die diagonaal van die vierkantige basis van die piramide te vind. Dus, die diagonaal van die basis van die piramide is 9,8 * 2 = 19,6 cm. 
In hierdie piramidevoorbeeld is die diagonaal van die basis 19,6 cm. Daarom is die sy gelyk aan: 





Bereken die volume van 'n vierkantige piramide
Inhoud
`n Vierkantige piramide is `n driedimensionele figuur met `n vierkantige basis en driehoekige skuins wat op een punt bokant die basis ontmoet. In die geval dat 


Trappe
Metode 1 van 3: Bepaal die volume met die oppervlakte van die basis en die hoogte

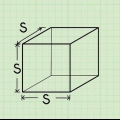
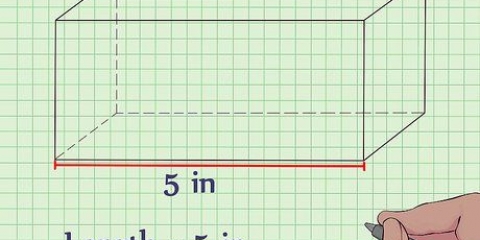
1. Meet die lengte van die kant van die basis. Aangesien vierkantige piramides per definisie `n vierkantige basis het, moet alle sye van die basis ewe lank wees. So met `n vierkantige piramide hoef jy net die lengte van een van die sye te ken.
- Gestel jy het `n piramide met `n vierkantige basis waarvan die sye `n lengte van het
. Jy sal hierdie waarde gebruik om die oppervlakte van die basis te bereken.
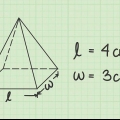
- As die sye van die basis nie ewe lank is nie, dan het jy `n reghoekige piramide in plaas van `n vierkantige piramide. Die formule vir die volume van `n reghoekige piramide is baie soortgelyk aan die formule vir vierkantige piramides. In die geval dat
is die lengte van die basis van die reghoekige piramide en
die breedte, dan die volume van die piramide
.

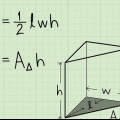
2. Bereken die oppervlakte van die basis. Om die volume te bepaal, benodig jy eers die oppervlakte van die basis. Jy doen dit deur die lengte en breedte van die basis te vermenigvuldig. Aangesien die basis van `n vierkantige piramide `n vierkant is, het alle sye dieselfde lengte, en die oppervlakte van die basis is gelyk aan die vierkant van die lengte van een van sy sye (dus vermenigvuldig met homself).


3. Vermenigvuldig die oppervlakte van die basis met die hoogte van die piramide. Dan vermenigvuldig jy die basisoppervlakte met die hoogte van die piramide. Ter herinnering, die hoogte is die afstand is die lengte van die lynstuk vanaf die bokant van die piramide tot by die basis, reghoekig.


4. Deel hierdie antwoord deur 3. Ten slotte bepaal jy die volume van die piramide deur die waarde wat jy sopas gevind het (deur die oppervlakte van die basis met die hoogte te vermenigvuldig) deur 3 te deel. Dit bereken die volume van die vierkantige piramide.
Metode 2 van 3: Bepaal die volume met die apotem

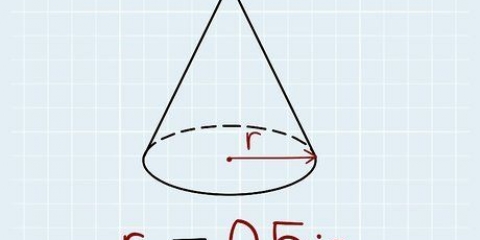
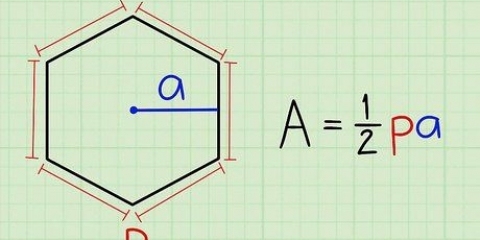
1. Meet die apotem van die piramide. Soms word die loodregte hoogte van die piramide nie gegee nie (of jy moet dit meet), maar die apoteem. Met die apotem kan jy die gebruik Pythagoras-stelling gebruik om loodregte hoogte te bereken.
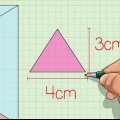
- Die apoteem van `n piramide is die afstand vanaf die toppunt na die middel van een van die sye van sy basis. Meet na die middel van een van die kante en nie na een van die hoeke van die basis nie. Vir hierdie voorbeeld neem ons aan dat apotem 13 cm is en die lengte van een kant van die basis is 10 cm.
- Onthou dat die Pythagoras-stelling as die vergelyking uitgedruk kan word
, waardeur
en
die loodregte bene is van die regte driehoek en
die skuinssy.

2. Stel jou `n reghoekige driehoek voor. Om die Pythagoras-stelling te gebruik, benodig jy `n reghoekige driehoek. Stel jou `n driehoek voor wat die piramide in die helfte verdeel en loodreg op die basis van die piramide. Die apotem van die piramide, genoem  , is die skuinssy van hierdie reghoekige driehoek. Die basis van hierdie reghoekige driehoek is die helfte van die lengte van
, is die skuinssy van hierdie reghoekige driehoek. Die basis van hierdie reghoekige driehoek is die helfte van die lengte van  , die sy van die vierkantige basis van die piramide.
, die sy van die vierkantige basis van die piramide.
 , is die skuinssy van hierdie reghoekige driehoek. Die basis van hierdie reghoekige driehoek is die helfte van die lengte van
, is die skuinssy van hierdie reghoekige driehoek. Die basis van hierdie reghoekige driehoek is die helfte van die lengte van  , die sy van die vierkantige basis van die piramide.
, die sy van die vierkantige basis van die piramide.
3. Ken veranderlikes aan die waardes toe. Die Pythagoras-stelling gebruik die veranderlikes a, b en c, maar dit is nuttig om dit te vervang met veranderlikes wat betekenisvol is vir jou probleem. die apotem  neem die plek in van
neem die plek in van  in die Pythagoras-stelling. Die been van die regte driehoek (
in die Pythagoras-stelling. Die been van die regte driehoek ( ), neem die plek in van
), neem die plek in van  Jy gaan die hoogte
Jy gaan die hoogte  bepaal die piramide, wat die plek inneem van
bepaal die piramide, wat die plek inneem van  in die Pythagoras-stelling.
in die Pythagoras-stelling.
 neem die plek in van
neem die plek in van  in die Pythagoras-stelling. Die been van die regte driehoek (
in die Pythagoras-stelling. Die been van die regte driehoek ( ), neem die plek in van
), neem die plek in van  Jy gaan die hoogte
Jy gaan die hoogte  bepaal die piramide, wat die plek inneem van
bepaal die piramide, wat die plek inneem van  in die Pythagoras-stelling.
in die Pythagoras-stelling.


4. Gebruik die Pythagoras-stelling om die loodregte hoogte te bereken. Gebruik die gemete waardes  en
en  . Los dan die vergelyking op:
. Los dan die vergelyking op:
 en
en  . Los dan die vergelyking op:
. Los dan die vergelyking op: .....(oorspronklike vergelyking)
.....(oorspronklike vergelyking) .....(vierkant albei kante)
.....(vierkant albei kante) .....(tik waardes in)
.....(tik waardes in) .....(vereenvoudig breuk)
.....(vereenvoudig breuk) .....(vereenvoudig vierkant)
.....(vereenvoudig vierkant) .....(trek af)
.....(trek af) .....(vereenvoudig wortel)
.....(vereenvoudig wortel)
5. Gebruik hoogte en basis om volume te bereken. Nadat jy hierdie berekeninge op die Pythagoras-stelling toegepas het, het jy nou die inligting wat jy nodig het om die volume van die piramide te bereken. Gebruik die formule  en los dit op, maak seker dat jy die antwoord in vierkante eenhede gee.
en los dit op, maak seker dat jy die antwoord in vierkante eenhede gee.
 en los dit op, maak seker dat jy die antwoord in vierkante eenhede gee.
en los dit op, maak seker dat jy die antwoord in vierkante eenhede gee.



Metode 3 van 3: Bepaal die volume met die hoogte van die bene

1. Meet die hoogte van die bene van die piramide. Die hoogte van die bene is die lengte van die rande van die piramide, gemeet van bo na een van die hoeke van die basis. Soos hierbo, gebruik die Pythagoras-stelling om die loodregte hoogte van die piramide te bereken.
- In hierdie voorbeeld neem ons aan dat die hoogte van die bene 11 cm is en dat die loodregte hoogte 5 cm is.

2. Stel jou `n reghoekige driehoek voor. Weereens het jy `n reghoekige driehoek nodig om die Pythagorese Stelling te kan gebruik. In hierdie geval is die onbekende waarde egter die basis van die piramide. Bekend is die vertikale hoogte en die hoogte van die bene. Stel jou nou voor dat jy die piramide skuins van een hoek na die ander sny, en dan die figuur oopmaak, die resulterende vlak sal soos `n driehoek lyk. Die hoogte van daardie driehoek is die loodregte hoogte van die piramide. Dit verdeel die blootgestelde driehoek in twee simmetriese reghoekige driehoeke. Die skuinssy van elk van die reghoekige driehoeke is die hoogte van die bene van die piramide. Die basis van elk van die reghoekige driehoeke is die helfte van die diagonaal van die basis van die piramide.

3. Ken veranderlikes toe. Gebruik die denkbeeldige reghoekige driehoek en ken waardes toe aan die Pythagoras-stelling. Jy ken die vertikale hoogte,  wat een kant van die Pythagoras-stelling is,
wat een kant van die Pythagoras-stelling is,  . Die hoogte van die bene van die piramide,
. Die hoogte van die bene van die piramide,  vorm die skuinssy van hierdie denkbeeldige reghoekige driehoek, en neem dus die plek in van
vorm die skuinssy van hierdie denkbeeldige reghoekige driehoek, en neem dus die plek in van  . Die onbekende hoeklyn van die basis van die piramide is die oorblywende sy van die regte driehoek,
. Die onbekende hoeklyn van die basis van die piramide is die oorblywende sy van die regte driehoek,  Nadat u hierdie vervangings gemaak het, lyk die vergelyking soos volg:
Nadat u hierdie vervangings gemaak het, lyk die vergelyking soos volg:
 wat een kant van die Pythagoras-stelling is,
wat een kant van die Pythagoras-stelling is,  . Die hoogte van die bene van die piramide,
. Die hoogte van die bene van die piramide,  vorm die skuinssy van hierdie denkbeeldige reghoekige driehoek, en neem dus die plek in van
vorm die skuinssy van hierdie denkbeeldige reghoekige driehoek, en neem dus die plek in van  . Die onbekende hoeklyn van die basis van die piramide is die oorblywende sy van die regte driehoek,
. Die onbekende hoeklyn van die basis van die piramide is die oorblywende sy van die regte driehoek,  Nadat u hierdie vervangings gemaak het, lyk die vergelyking soos volg:
Nadat u hierdie vervangings gemaak het, lyk die vergelyking soos volg:


4. Bereken die diagonaal van die vierkantige basis. Jy moet die vergelyking herrangskik om die veranderlike te kry  isoleer, en bereken dan die waarde daarvan.
isoleer, en bereken dan die waarde daarvan.
 isoleer, en bereken dan die waarde daarvan.
isoleer, en bereken dan die waarde daarvan. ..........(aangepaste vergelyking)
..........(aangepaste vergelyking) ..........(vervang h aan beide kante)
..........(vervang h aan beide kante) ..........(trek die vierkantswortel van beide kante af)
..........(trek die vierkantswortel van beide kante af) ..........(vul die nommers in)
..........(vul die nommers in) ..........(vereenvoudig die vierkante)
..........(vereenvoudig die vierkante) ..........(trek waardes af)
..........(trek waardes af) ..........(vereenvoudig die vierkantswortel)
..........(vereenvoudig die vierkantswortel)
5. Vind die kant van die basis van die diagonaal. Die basis van die piramide is `n vierkant. Die diagonaal van elke vierkant is gelyk aan die lengte van een van sy sye, keer vierkantswortel 2. En so kan jy die sy van `n vierkant vind deur die diagonaal deur vierkantswortel 2 te deel.


6. Bereken die volume deur die kant en hoogte te gebruik. Keer terug na die oorspronklike formule om volume te bereken deur sy en loodregte hoogte te gebruik.




Wenke
- In `n vierkantige piramide kan die loodregte hoogte, apotem en die lengte van die rand van die basis alles bereken word deur die Pythagoras-stelling te gebruik.
Artikels oor die onderwerp "Bereken die volume van 'n vierkantige piramide"
Оцените, пожалуйста статью
Soortgelyk
Gewilde