Hierdie proses is basies dieselfde as om eers die oppervlakte van die basis te bereken en dan hierdie area te vermenigvuldig met die hoogte van die kubus (of met ander woorde lengte × breedte × hoogte), want die oppervlakte van die basis word bepaal deur die lengte met die breedte te vermenigvuldig. Aangesien die lengte, breedte en hoogte van `n kubus gelyk is, kan ons die proses vereenvoudig deur een van hierdie waardes tot die derde mag te verhoog. Kom ons gaan voort met ons voorbeeld. Die lengte van die rand was 2 cm, so die volume van die kubus is 2 x 2 x 2 (of 2)= 8. 
In ons voorbeeld is die lengte van die rib in sentimeter gegee, dus moet die antwoord in gestel word kubieke sentimeter. Die antwoord is dus 8 cm. 

So in ons voorbeeld deel ons vyftig deur ses: 50/6 = 8,33 cm. Onthou dat die eenhede van tweedimensionele antwoorde kwadraat geskryf word (cm, m ensovoorts). 
In ons voorbeeld, √8.33 = 2,89 cm. 
So in ons voorbeeld: 2.89 × 2.89 × 2.89 = 24,14 cm. Moenie vergeet om die antwoord in kubieke eenhede te skryf nie. 

Dit kan ook uit die Pythagoras-stelling afgelei word. d, d en l vorm `n gelyksydige driehoek met D as skuinssy, dus d = d + l. Ons het vroeër reeds bepaal: d = 2l, dus kan ons ook die volgende sê: d = 2l + l = 3l. Gestel ons weet dat die lengte van die diagonaal wat van een hoek in die basis van die kubus na die teenoorgestelde hoek in die boonste vlak van die kubus loop, 10 meter is. As ons dus die volume wil bereken, voer ons 10 in die formule hierbo in vir d. d = 3l. 10 = 3l. 100 = 3l 33.33 = l 5.77 m = l. Van hierdie punt af kan ons die volume bereken deur die lengte van die rib na die kubus te verhoog. 5.77 = 192.45 m
Bereken die volume van 'n kubus
Inhoud
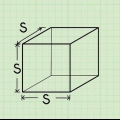
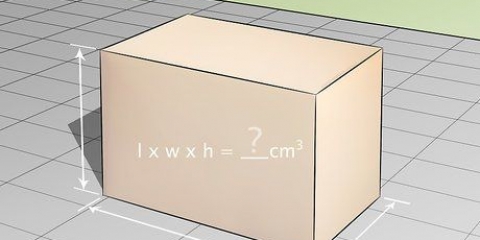
`n Kubus is `n driedimensionele figuur waarvan die lengte, breedte en hoogte gelyk is. ’n Kubus het ses vierkante vlakke waarvan die sye ewe lank en loodreg op mekaar is. Om die volume van `n kubus te bereken is baie eenvoudig - gewoonlik hoef jy net die volgende te vermenigvuldig: lengte × breedte × hoogte. Omdat die rande van `n kubus almal dieselfde lengte het, kan jy ook die volume van `n kubus soos volg sien: l, waardeur l is die lengte van een van die rande van die kubus. Gaan na stap 1 vir `n gedetailleerde verduideliking.
Trappe
Metode 1 van 3: Lig die rand van die kubus na die kubus op

1. Vind die lengte van een van die rande van die kubus. Dikwels sal jy `n som sien waar die lengte van een van die ribbes reeds gegee is. Sodra jy hierdie inligting het, het jy alles wat jy nodig het om die kubus se volume te bepaal. Gebruik `n liniaal of maatband as jy nie `n wiskundeprobleem oplos nie, maar net die volume van `n bestaande kubusvormige voorwerp wil weet.
- Om die proses om die volume van `n kubus te bepaal beter te verstaan, kom ons begin met `n voorbeeldsom terwyl ons deur die stappe in hierdie afdeling stap. Gestel dat die rand van die kubus 2 cm lank is. Ons gaan hierdie inligting in die volgende stap gebruik om die volume van die kubus te bepaal.

2. Verhoog die lengte van die rib tot die derde mag. Sodra jy die lengte van een van die ribbes het, verhoog dan hierdie getal tot die derde mag. Met ander woorde, vermenigvuldig die getal twee keer met homself. as l is die lengte van die rib, dan vermenigvuldig jy l × l × l (of in eenvoudiger vorm l). Die resultaat is die volume van die kubus.

3. Gee jou antwoord in kubieke eenhede. Volume is die maatstaf van `n driedimensionele ruimte, dus moet die oplossing in kubieke eenhede geskryf word. Op `n toets kan dit jou punte kos as jy nie die antwoord korrek in kubieke eenhede gee nie, so moenie vergeet nie!
Metode 2 van 3: Bepaal volume volgens oppervlakte

1. Vind die area van die gesigte van jou kubus. Die maklikste manier om volume te bepaal is deur die rib na die kubus te lig, maar dit is nie die enige manier. Die lengte van die rand van `n kubus of die oppervlakte van een van sy vlakke kan afgelei word van verskeie ander eienskappe van die kubus, wat beteken dat as jy met hierdie inligting begin, jy die volume van die kubus op `n afgeleide manier kan bepaal. Byvoorbeeld, as jy net die totale oppervlakte van al die sye van die kubus ken, kan jy die volume vind deur hierdie area deur ses te deel en dan die vierkantswortel van daardie getal te neem om die lengte van die rand te vind. Van daardie punt af kan jy weer tot die derde mag styg. In hierdie afdeling loop ons stap vir stap deur hierdie proses.
- Die oppervlakte van `n kubus word deur die formule gegee 6l, waardeur l is die lengte van een van die rande van die kubus. Hierdie formule is eintlik dieselfde as om die tweedimensionele area van een van die kante van die kubus te bepaal, en dan die ses (gelyke) areas by te voeg. Ons sal hierdie formule gebruik om die volume van die kubus uit die area van die kubus te bepaal.
- Gestel ons het `n kubus waarvan ons weet dat die area 50 cm is, maar ons weet nie wat die lengte van die ribbes is nie. In die volgende stappe sal ons hierdie inligting gebruik om die volume van die kubus te vind.

2. Verdeel die oppervlakte van die kubus deur ses. Aangesien die kubus ses vlakke van gelyke oppervlakte het, kan ons die oppervlakte van `n gesig bepaal deur die oppervlakte van die kubus deur ses te deel. Die oppervlakte van `n vlak is dieselfde as die vermenigvuldiging van twee rande (l × b, b × h, of h × l).

3. Vind die vierkantswortel van hierdie waarde. Aangesien die oppervlakte van een van die vlakke van `n kubus gelyk is aan l (l × l), kan ons nou die vierkantswortel van die gevonde waarde neem om die lengte van een van die ribbes te bepaal. Sodra jy dit weet het jy genoeg inligting om die volume van die kubus soos gewoonlik te bereken.

4. Verhoog hierdie getal tot die derde mag om die kubus se volume te vind. Noudat jy `n waarde vir die lengte van die ribbes bepaal het, kan jy hierdie getal na die kubus verhoog om die volume te bepaal soos beskryf in die eerste afdeling van hierdie artikel.
Metode 3 van 3: Bepaal die volume deur diagonale te gebruik

1. Verdeel die diagonaal van een van die vlakke van die kubus deur √2 om die lengte van die kubus se rande te vind. Die diagonaal van `n vierkant is √2 × die lengte van een van sy rande. Met ander woorde, as jy net die waarde van een van die hoeklyne van `n vlak van die kubus ken, kan jy die lengte van die kante van die kubus bereken deur hierdie waarde deur √2 te deel. Van daardie punt af kan jy weer tot die derde mag verhoog en die volume bepaal soos hierbo beskryf.
- Gestel een van die vlakke van die kubus het `n diagonaal van7 meter lank. Dan kan ons die lengte van een van die ribbes bereken deur 7 deur √2 te deel. 7/√2 = 4,96 meter. Noudat ons die lengte van die kante van die kubus ken, kan ons die volume van die kubus bereken deur 4.96 na die kubus te verhoog: 4.96 = 122,36 meter.
- Gee aandag: d = 2l, waar d is die lengte van die diagonaal van een van die vlakke van die kubus en l is die lengte van een van die rande van die kubus. Dit kan afgelei word van die Pythagoras-stelling, waar die kwadraat van die skuinssy van `n gelyksydige driehoek gelyk is aan die som van die kwadraat van die ander twee sye. Aangesien die diagonaal van `n vlak van `n kubus `n gelyksydige driehoek vorm met twee van die rande van daardie vlak, kan ons die volgende sê: d = l + l = 2l.

2. Vind die vierkant van die diagonaal tussen twee teenoorstaande hoeke van die kubus, deel deur drie en neem die vierkantswortel om die lengte van een van die rande te vind. As die lengte van die driedimensionele lyn tussen twee teenoorstaande hoeke van die kubus die enigste gegewe is, kan jy steeds die volume van die kubus bepaal. d vorm een van die sye van `n gelyksydige driehoek waarvan die skuinssy die lyn tussen twee teenoorgestelde hoeke van die kubus is, dus kan ons sê: d = 3l, waar D die driedimensionele lyn tussen twee teenoorstaande hoeke van die kubus is.
Artikels oor die onderwerp "Bereken die volume van 'n kubus"
Оцените, пожалуйста статью
Gewilde