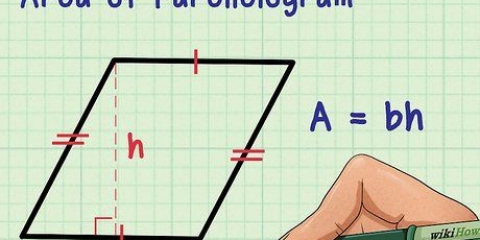Hoe om die volume van 'n piramide te bereken: 8 stappe (met prente)

Inhoud

Trappe
- Metode 1 van 2: Piramide met `n reghoekige basis
- Metode 2 van 2: Piramide met `n driehoekige basis
Wenke
Waarskuwings

Om die volume van `n piramide te bereken, vermenigvuldig die oppervlakte van die basis met die hoogte van die piramide. Deel die resultaat deur 3, dit is al! Lees hierdie artikel met berekeningsmetodes vir `n piramide met `n reghoekige basis en `n piramide met `n driehoekige basis.

Trappe

Metode 1 van 2: Piramide met `n reghoekige basis

Prent getiteld Bereken die volume van `n piramide Stap 1

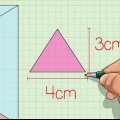
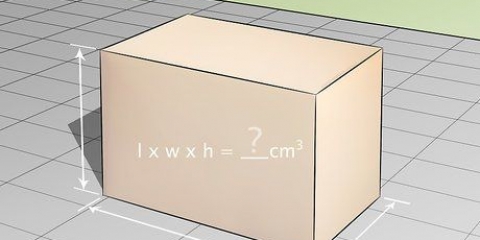
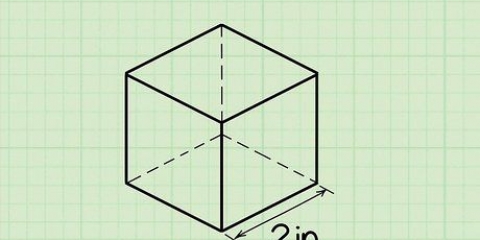
1. Bepaal die lengte en breedte van die basis. In hierdie voorbeeld is die lengte 4 cm en die breedte 3 cm. As jy `n vierkantige basis het, is die metode dieselfde, net die lengte en breedte is gelyk. Skryf jou afmetings neer.

Prent getiteld Bereken die volume van `n piramide Stap 2

2. Vermenigvuldig die lengte met die breedte om die oppervlakte van die basis te bereken. Om die oppervlakte van ons voorbeeld te bereken, vermenigvuldig ons 3 cm met 4 cm. 3cm x 4cm = 12cm

Prent getiteld Bereken die volume van `n piramide Stap 3

3. Vermenigvuldig die oppervlakte van die basis met die hoogte. Die oppervlakte van die basis is 12 cm en die hoogte is 4 cm, so ons vermenigvuldig 12 cm met 4 cm. 12cm x 4cm = 48cm

Prent getiteld Bereken die volume van `n piramide Stap 4

4. Deel die resultaat deur 3. Dit is dieselfde as om met 1/3 te vermenigvuldig. 48cm/3 = 16cm. Die volume van `n piramide met `n hoogte van 4 cm en `n reghoekige basis met `n breedte van 3 cm en `n lengte van 4 cm is dus 16 cm. Moenie vergeet om die uitkoms in kubieke eenhede aan te dui nie.

Metode 2 van 2: Piramide met `n driehoekige basis

Prent getiteld Bereken die volume van `n piramide Stap 5

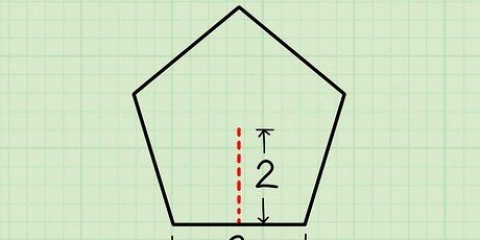
1. Bepaal die lengte en breedte van die basis. Die lengte en breedte van die basis moet loodreg op mekaar, anders sal hierdie metode nie werk nie. Hulle kan ook gesien word as die onderkant en die hoogte van die driehoek. In hierdie voorbeeld is die breedte van die driehoek 2 cm en die lengte is 4 cm. Skryf dit neer.

Prent getiteld Bereken die volume van `n piramide Stap 6

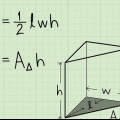
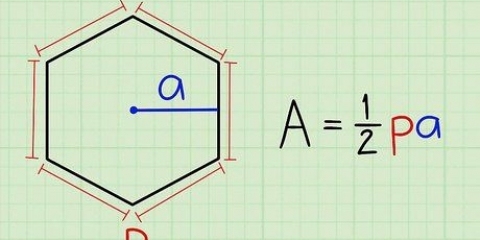
2. Bereken die oppervlakte van die basis. Om die oppervlakte van die basis te bereken, gebruik ons die volgende formule:A = 1/2(o)(h). Dit is hoe ons dit doen:

A = 1/2(o)(h)

A = 1/2(2)(4)

A = 1/2(8)

A = 4 cm

Prent getiteld Bereken die volume van `n piramide Stap 7

3. Vermenigvuldig die oppervlakte van die basis met die hoogte van die piramide. Die oppervlakte van die basis is 4 cm en die hoogte is 5 cm. 4cm x 5cm = 20cm.

Prent getiteld Bereken die volume van `n piramide Stap 8

4. Deel die resultaat deur 3. 20cm/3 = 6.67cm. Die volume van `n piramide met `n hoogte van 5 cm en `n driehoekige basis met `n breedte van 2 cm en `n lengte van 4 cm is dus 6,67 cm.

Wenke

In `n piramide met `n vierkantige basis word die hoogte, die lyn wat die driehoekige sy in twee gelyke driehoeke verdeel, en die breedte van die basis verbind deur die Pythagoras-stelling: (breedte ÷ 2) + (hoogte) = (hoogte van driehoek)
Hierdie metode kan ook toegepas word op voorwerpe soos vyfhoekige piramides, seskantige piramides, ens. Die algemene proses is: A) bereken die oppervlakte van die basis; B) meet die hoogte vanaf die bokant van die piramide tot by die middel van die basis; C) vermenigvuldig A met B; D) deel deur 3.
Alles gewone piramides is die regop ribbes, die lyn wat die driehoekige sy in twee gelyke driehoeke verdeel en die breedte van die basis verbind deur die Pythagoras-stelling: (lengte van die sy ÷ 2) + (lengte van rib) = (hoogte)

Waarskuwings

Piramides het drie tipes hoogtes: die lyn wat die driehoekige gesig in twee gelyke driehoeke verdeel, die lengte van die rib (langs die sy van `n driehoekige gesig) en die werklike hoogte (vanaf die punt van die piramide loodreg af na die basis) . ).