Hoe om die oppervlakte van 'n vyfhoek te bereken

Inhoud

Trappe
Wenke

`n Vyfhoek is `n veelhoek met vyf reguit sye. Byna alle probleme wat jy in wiskundeklas sal teëkom, sal gereelde vyfhoeke behels, met vyf gelyke sye. Daar is twee algemene maniere om die oppervlakte te bereken, afhangende van hoeveel inligting jy het.

Trappe

Metode 1 van 3: Bepaal die area deur die kante en die apotem te gebruik

Prent getiteld Vind die area van `n gewone vyfhoek Stap 1

1. Begin met die lengte van die sy en apotem. Hierdie metode werk vir gereelde vyfhoeke, met vyf gelyke sye. Benewens die lengte van die sy het jy die `apothema` van die vyfhoek nodig. Die apoteem is die lyn vanaf die middel van die vyfhoek na `n sy, wat die sy loodreg sny (d.w.s. teen `n hoek van 90º).

Moenie die apotem met die radius van `n veelhoek verwar nie, want dit sny `n hoek (hoekpunt) in plaas van `n punt in die middel van die sy. As jy net die lengte van `n sy en die radius ken, gaan voort na die volgende metode.
As voorbeeld gebruik ons `n vyfhoek met sy 3 en apotem 2.

Prent getiteld Vind die area van `n gewone vyfhoek Stap 2

2. Verdeel die vyfhoek in vyf driehoeke. Trek vyf lyne vanaf die middel van die vyfhoek wat elkeen na `n hoekpunt (hoek) lei. Jy het nou vyf driehoeke.

Prent getiteld Vind die area van `n gewone vyfhoek Stap 3

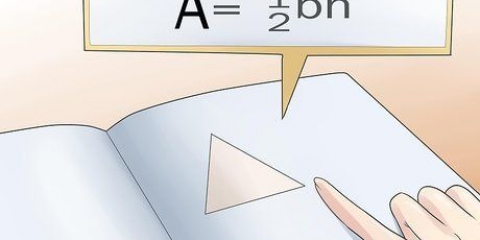
3. Bereken die oppervlakte van `n driehoek. Elke driehoek het `n basis gelyk aan die sy van die vyfhoek. Dit het ook `n hoogte wat gelyk is aan die apotem. (Onthou, die hoogte van `n driehoek is die lengte van die sy wat loodreg op sy basis is en na `n hoekpunt strek). Om die oppervlakte van `n driehoek te bereken, gebruik jy ½ x basis x hoogte.

In ons voorbeeld is die oppervlakte van die driehoek=½ x 3 x 2=3.

Prent getiteld Vind die area van `n gewone vyfhoek Stap 4

4. Vermenigvuldig met vyf vir die totale oppervlakte van die vyfhoek. Ons het die vyfhoek in vyf gelyke driehoeke verdeel. Om die totale oppervlakte te bereken, vermenigvuldig die oppervlakte van `n driehoek met vyf.

In ons voorbeeld, A(totaal van die vyfhoek)=5 x A(driehoek)=5 x 3=15.

Metode 2 van 3: Bepaal die oppervlakte deur die lengte van `n sy te gebruik

Prent getiteld Vind die area van `n gewone vyfhoek Stap 5

1. Begin met die lengte van een kant. Hierdie metode werk net vir gereelde vyfhoeke, wat vyf sye van gelyke lengte het.

In hierdie voorbeeld gebruik ons `n vyfhoek met lengte 7 vir elke kant.

Prent getiteld Vind die area van `n gewone vyfhoek Stap 6

2. Verdeel die vyfhoek in vyf driehoeke. Trek `n lyn van die middel van die vyfhoek na `n hoekpunt. Herhaal vir elke hoekpunt. Jy het nou vyf driehoeke, elk van dieselfde grootte.

Prent getiteld Vind die area van `n gewone vyfhoek Stap 7

3. Verdeel `n driehoek in die helfte. Trek `n lyn vanaf die middel van die vyfhoek na die basis van `n driehoek. Hierdie lyn moet die basis teen `n regte hoek (90º) sny, wat die driehoek in twee gelyke, kleiner driehoeke verdeel.

Prent getiteld Vind die area van `n gewone vyfhoek Stap 8

4. Benoem een van die kleiner driehoeke. Ons kan reeds `n sy en `n hoek van die kleiner driehoek benoem:

Die basis van die driehoek is ½ keer die sy van die vyfhoek. In ons voorbeeld is dit ½ x 7=3.5 eenhede.

Die hoek in die middel van die vyfhoek is altyd 36º. (As jy 360º aanvaar vir `n volle sirkel, kan jy dit in 10 kleiner driehoeke verdeel. 360 ÷ 10=36, dus die hoek van so `n driehoek is 36º).

Prent getiteld Vind die area van `n gewone vyfhoek Stap 9

5. Bereken die hoogte van die driehoek. Die hoogte van hierdie driehoek is die sy loodreg op die sy van die vyfhoek wat na die middelpunt lei. Ons gebruik eenvoudige trigonometrie om die lengte van hierdie sy te bepaal:

In `n reghoekige driehoek is die is raaklyn van `n hoek gelyk aan die lengte van die teenoorgestelde sy, gedeel deur die lengte van die aangrensende sy.

Die sy teenoor die hoek van 36º is die basis van die driehoek (die helfte van die sy van die vyfhoek). Die aangrensende sy van die hoek van 36º is die hoogte van die driehoek.

tan(36º)=oorkant / aangrensend

In ons voorbeeld, tan(36º)=3.5 / hoogte

hoogte x bruin(36º)=3.5

hoogte=3,5 / bruin(36º)

hoogte = (ongeveer) 4.8.

Prent getiteld Vind die area van `n gewone vyfhoek Stap 10

6.Bereken die oppervlakte van die driehoek. Die oppervlakte van `n driehoek is gelyk aan ½ basis x hoogte. (A=½bh.) Noudat jy die hoogte ken, voer hierdie waardes in om die hoogte van jou klein driehoekie te bepaal.

In ons voorbeeld is die oppervlakte van een van die klein driehoeke=½bh=½(3.5)(4.8)=8.4.

Prent getiteld Vind die area van `n gewone vyfhoek Stap 11

7. Vermenigvuldig om die area van die vyfhoek te vind. Een van hierdie kleiner driehoeke dek 1/10 van die oppervlakte van die vyfhoek. Vir die totale oppervlakte, vermenigvuldig die oppervlakte van die kleiner driehoek met 10.

In ons voorbeeld is die oppervlakte van die hele vyfhoek=8.4 x 10=84.

Metode 3 van 3: Gebruik `n formule

Prent getiteld Vind die area van `n gewone vyfhoek Stap 12

1. Gebruik die uiteensetting en apotem. Die apoteem is `n lyn vanaf die middel van `n vyfhoek wat een kant teen `n regte hoek sny. As die lengte gegee word, kan jy hierdie eenvoudige formule gebruik.

Oppervlakte van `n gereelde vyfhoek =pa / 2, waar bl=die omtrek en a= die apotem.
As jy nie die omtrek ken nie, bereken dit deur die lengte van die sy te gebruik: p=5s, waar s die lengte van die sy is.

Prent getiteld Vind die area van `n gewone vyfhoek Stap 13

2. Gebruik die lengte van die sy. As jy net die lengte van die sye ken, gebruik die volgende formule:

Oppervlakte van `n gereelde vyfhoek = (5s ) / (4tan(36º)), waar s=lengte van een kant.

bruin(36º)=√(5-2√5). As jou sakrekenaar nie `n `tan`-funksie het nie, gebruik die formule vir die area: Area=(5s) / (4√(5-2√5)).

Prent getiteld Vind die area van `n gewone vyfhoek Stap 14

3. Kies `n formule wat slegs die radius gebruik. Jy kan selfs die area vind as jy net die radius ken. Gebruik die volgende formule:

Die oppervlakte van `n gereelde vyfhoek = (5/2)rsonde(72º), waar r die radius is.

Wenke

Onreëlmatige vyfhoeke of vyfhoeke met ongelyke sye is moeiliker om te bestudeer. Die beste benadering is gewoonlik om die vyfhoek in driehoeke te verdeel en die oppervlaktes van al die driehoeke bymekaar te tel. Miskien moet jy ook `n groter vorm om die vyfhoek teken, die oppervlakte daarvan bereken en dan die oppervlakte van die ekstra spasie aftrek.
Indien moontlik, gebruik beide `n meetkundige metode en `n formule, en vergelyk die resultate om jou antwoord te kontroleer. Die antwoorde kan effens verskil as jy die formule op een slag heeltemal invul (want dan ontbreek die stappe waarin jy voltooi), maar hulle behoort baie naby aan mekaar te wees.
Die voorbeelde wat hier gegee word, gebruik afgeronde waardes om hul wiskunde makliker te maak. As jy `n regte veelhoek met die gegewe sylengtes het, sal jy effens verskillende resultate vir die ander lengtes en oppervlakte kry.
Die formules is afgelei van meetkundige metodes, soortgelyk aan dié wat hier beskryf word. Probeer om self uit te vind hoe om hulle aandag af te lei. Die radiusformule is moeiliker om af te lei as die ander (wenk: jy het die dubbelhoek-identiteit nodig).