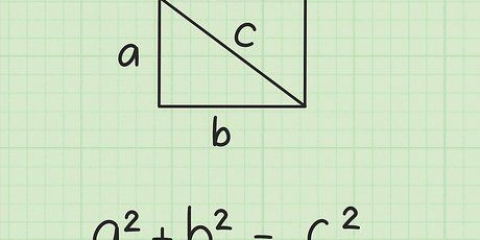
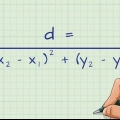Die twee korter sye van die driehoek is die sye van die vierkant: elkeen het `n lengte s. Die skuinssy is die diagonaal van die vierkant, d. 


Vereenvoudig: 
Deel beide kante deur twee: 
Area = 
Area = 

Gestel byvoorbeeld `n vierkant het `n diagonaal van 10 cm. Area = 
=
= 50 cm. Byvoorbeeld, `n vierkant met `n diagonaal van 10 cm het sye van lengte  cm.
cm. As jy beide die lengte van `n sy en die oppervlakte van die diagonaal wil vind, kan jy eers hierdie formule gebruik en dan die antwoord vir die area vierkantig maak: Oppervlakte  cm. Dit is ietwat minder akkuraat, want
cm. Dit is ietwat minder akkuraat, want  is `n irrasionale getal wat afrondingsfoute kan hê.
is `n irrasionale getal wat afrondingsfoute kan hê. Teken `n vierkant op papier. Maak seker dat alle kante gelyk is. Meet die diagonaal. Teken `n tweede vierkant met daardie lengte as die sye van die vierkant. Trek `n kopie van jou eerste vierkant na sodat jy twee het. Knip al drie blokkies uit. Sny die twee kleiner blokkies in vorms wat binne die groot vierkant pas. Hulle moet die spasie perfek vul om te wys dat die oppervlakte van die groot vierkant presies twee keer die oppervlakte van die kleiner vierkant is.
Bereken die oppervlakte van 'n vierkant deur die diagonaal te gebruik
Inhoud
Die mees algemene formule vir die oppervlakte van `n vierkant is eenvoudig: dit is die lengte van een van sy sye kwadraat, of s. Maar soms ken jy net die lengte van die diagonaal van `n vierkant, die lyn tussen twee teenoorgestelde hoekpunte. As jy vertroud is met reghoekige driehoeke, kan jy `n nuwe formule aflei met die diagonaal as die enigste veranderlike.
Trappe
Deel 1 van 2: Bereken die oppervlakte van `n vierkant

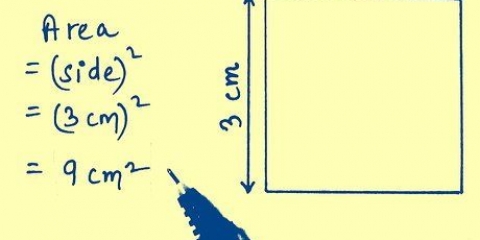
1. Teken jou vierkant. `n Vierkant het vier gelyke sye. Kom ons sê elke kant het `n lengte van `s`.

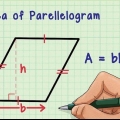
2. Gebruik die standaardformule vir die oppervlakte van `n vierkant. Die oppervlakte van `n vierkant is gelyk aan sy lengte keer sy breedte. Want elke kant s dit word formule Oppervlakte = s x s = s. Dit sal binnekort nuttig blyk te wees.

3. Verbind twee teenoorgestelde hoeke om `n diagonaal te maak. Die maat van hierdie diagonaal word d eenhede. Hierdie diagonaal verdeel die vierkant in twee reghoekige driehoeke.

4.Gebruik die Pythagoras-stelling vir een van die driehoeke. Die Pythagoras-stelling is `n formule om die skuinssy (langste sy) van `n reghoekige driehoek te vind: (sy A) + (sy B) = (skuinssy) of  . Noudat die vierkant in die helfte gedeel is, kan jy hierdie formule op een van die regte driehoeke gebruik:
. Noudat die vierkant in die helfte gedeel is, kan jy hierdie formule op een van die regte driehoeke gebruik:
 . Noudat die vierkant in die helfte gedeel is, kan jy hierdie formule op een van die regte driehoeke gebruik:
. Noudat die vierkant in die helfte gedeel is, kan jy hierdie formule op een van die regte driehoeke gebruik:

5. Rangskik die vergelyking sodat s aan die een kant is. Onthou dat ons weet dat die oppervlakte van die vierkant s is. As jy s aan die een kant kan isoleer, dan het jy `n nuwe vergelyking vir die area:






6. Gebruik hierdie formule met `n voorbeeldvierkant. Hierdie stappe het bewys dat die formule Area =  van toepassing op alle blokkies. Voer die lengte van die diagonaal in vir d en oplos.
van toepassing op alle blokkies. Voer die lengte van die diagonaal in vir d en oplos.
 van toepassing op alle blokkies. Voer die lengte van die diagonaal in vir d en oplos.
van toepassing op alle blokkies. Voer die lengte van die diagonaal in vir d en oplos.
=

= 50 cm.
Deel 2 van 2: Bykomende inligting
1. Vind die diagonaal van die lengte van `n sy. Die Pythagoras-stelling vir `n vierkant met sy s en diagonaal d gee jou die formule  aan. Los op vir `d` as jy die lengtes van die sye ken en die lengte van die diagonaal wil bepaal:
aan. Los op vir `d` as jy die lengtes van die sye ken en die lengte van die diagonaal wil bepaal:
 aan. Los op vir `d` as jy die lengtes van die sye ken en die lengte van die diagonaal wil bepaal:
aan. Los op vir `d` as jy die lengtes van die sye ken en die lengte van die diagonaal wil bepaal: - Byvoorbeeld, as `n vierkant sye van 7 cm het, dan is die diagonaal d = 7√2 cm, of ongeveer 9,9 cm.
- As jy nie `n sakrekenaar het nie, kan jy 1.4 gebruik as `n skatting van √2.
2. Bepaal die lengte van `n sy deur die diagonaal te gebruik. Is die diagonaal gegee en jy weet dat die diagonaal van `n vierkant  dan kan jy beide kante verdeel deur
dan kan jy beide kante verdeel deur  aan
aan  om te kry.
om te kry.
 dan kan jy beide kante verdeel deur
dan kan jy beide kante verdeel deur  aan
aan  om te kry.
om te kry. cm.
cm. cm. Dit is ietwat minder akkuraat, want
cm. Dit is ietwat minder akkuraat, want  is `n irrasionale getal wat afrondingsfoute kan hê.
is `n irrasionale getal wat afrondingsfoute kan hê.3. Interpreteer die oppervlakformule. Die formule Area =  blyk wiskundig korrek te wees, maar is daar `n manier om dit direk te toets? Wel,
blyk wiskundig korrek te wees, maar is daar `n manier om dit direk te toets? Wel,  is die oppervlakte van `n tweede vierkant met die diagonaal as sy. Omdat die volledige formule
is die oppervlakte van `n tweede vierkant met die diagonaal as sy. Omdat die volledige formule  jy kan redeneer dat hierdie tweede vierkant presies twee keer die oppervlakte van die oorspronklike vierkant het. Jy kan dit self toets:
jy kan redeneer dat hierdie tweede vierkant presies twee keer die oppervlakte van die oorspronklike vierkant het. Jy kan dit self toets:
 blyk wiskundig korrek te wees, maar is daar `n manier om dit direk te toets? Wel,
blyk wiskundig korrek te wees, maar is daar `n manier om dit direk te toets? Wel,  is die oppervlakte van `n tweede vierkant met die diagonaal as sy. Omdat die volledige formule
is die oppervlakte van `n tweede vierkant met die diagonaal as sy. Omdat die volledige formule  jy kan redeneer dat hierdie tweede vierkant presies twee keer die oppervlakte van die oorspronklike vierkant het. Jy kan dit self toets:
jy kan redeneer dat hierdie tweede vierkant presies twee keer die oppervlakte van die oorspronklike vierkant het. Jy kan dit self toets:Wenke
- Hierdie eenvoudige vergelyking word in baie velde gebruik, insluitend kristallografie, chemie en kuns. Byvoorbeeld, jy kan dit gebruik om die oppervlakte van `n landskap wat jy sien tydens opmeting te bereken, of wanneer jy perspektief in fotografie of skilderkuns gebruik, deur die afstand wat jy gestap het te meet en `n rooster van daardie afstand as die diagonaal voor te stel.
- As jy `n meer visuele benadering tot wiskunde wil volg, of leer hoe om grafieke en grafieke in kuns te gebruik, of die spiraalpad van `n deeltjie wil verken, kyk na `n paar artikels oor Microsoft Excel, wiskunde, sigblaaie en grafika.
- As jy nie `n sakrekenaar het nie, maar `n meer akkurate skatting van die vierkantswortel van twee benodig, is daar maniere om om dit met die hand te doen. `n Voorbeeld hiervan is die Newton-Raphson-metode.
Artikels oor die onderwerp "Bereken die oppervlakte van 'n vierkant deur die diagonaal te gebruik"
Оцените, пожалуйста статью
Soortgelyk
Gewilde