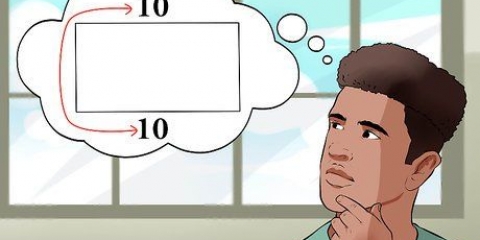
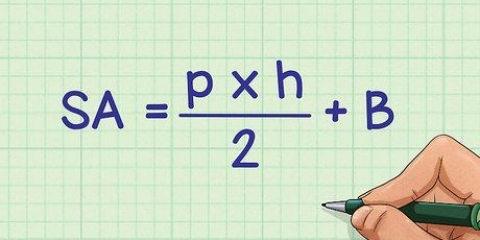Byvoorbeeld, as `n vlieër twee diagonale van 7 cm en 10 cm het, sal jou formule soos volg lyk: .
. 
Byvoorbeeld:



Byvoorbeeld:


Die oppervlakte van `n vlieër met diagonale van 10 cm en 7 cm is dus 35 vierkante cm. 

Byvoorbeeld, as jou vlieër `n sy van 20 cm en `n sy van 15 cm het, sal jou formule soos volg lyk:  .
. 
Byvoorbeeld:



Byvoorbeeld: as die hoek  dan sal jou formule soos volg lyk:
dan sal jou formule soos volg lyk:  .
. 
Byvoorbeeld, die sinus van `n 150 grade hoek is 0,5, so jou formule sal soos volg lyk:  .
. 
Byvoorbeeld:


Die oppervlak van `n vlieër, met twee sye van 20 cm en 15 cm, en die hoek tussen hulle van 150 grade, is dus 150 vierkante cm. 

Byvoorbeeld, as jou vlieër `n oppervlakte van 35 vierkante cm het, sal jou formule soos volg lyk:  .
. 
Byvoorbeeld, as jy weet dat een van die hoeklyne 7 cm lank is, sal jou formule soos volg lyk:  .
. 
Byvoorbeeld:




Byvoorbeeld:



Die lengte van die ontbrekende diagonaal van `n vlieër, gegewe `n oppervlakte van 35 vierkante cm en `n diagonaal van 7 cm, is dus 10 cm.
Bereken die oppervlakte van 'n vlieër
Inhoud
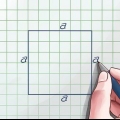
`n Vliër is `n tipe vierhoek met twee pare gelyke, aangrensende sye. Vlieërs kan die tradisionele voorkoms van `n vlieër hê, maar `n vlieër kan ook `n diamant of `n vierkant wees. Maak nie saak hoe `n vlieër lyk nie, die metodes om die oppervlak te vind sal dieselfde wees. As jy die lengte van die hoeklyne ken, kan jy die area deur eenvoudige wiskunde vind. Jy kan ook trigonometrie gebruik om die area te vind, as jy die sye en hoeke van die figuur ken.
Trappe
Metode 1 van 3: Gebruik die hoeklyne om die oppervlakte te bepaal

1. Skryf die formule vir die oppervlakte van `n vlieër, gegewe twee diagonale. Die formule is  , waardeur
, waardeur  is gelyk aan die oppervlakte van die vlieër, en
is gelyk aan die oppervlakte van die vlieër, en  en
en  gelyk aan die lengte van die vlieër se hoeklyne.
gelyk aan die lengte van die vlieër se hoeklyne.
 , waardeur
, waardeur  is gelyk aan die oppervlakte van die vlieër, en
is gelyk aan die oppervlakte van die vlieër, en  en
en  gelyk aan die lengte van die vlieër se hoeklyne.
gelyk aan die lengte van die vlieër se hoeklyne.
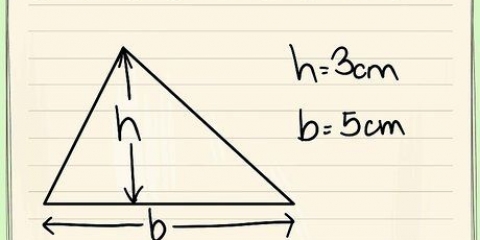
2. Pas die lengtes van die hoeklyne op die formule toe. ’n Diagonaal is ’n reguit lyn wat van een hoekpunt na die hoekpunt aan die ander kant loop. Jy moet óf die lengte van die hoeklyne kry óf hulle kan meet. As jy nie die lengte van die hoeklyne ken nie, kan jy nie hierdie metode gebruik nie.
 .
.
3. Vermenigvuldig die lengtes van die hoeklyne. Die produk word die nuwe toonbank in die area vergelyking.



4. Deel die produk van die hoeklyne deur 2. Dit sal jou die oppervlakte van die vlieër gee, in vierkante eenhede.


Die oppervlakte van `n vlieër met diagonale van 10 cm en 7 cm is dus 35 vierkante cm.
Metode 2 van 3: Gebruik `n hoek en twee sye om die oppervlakte te bepaal

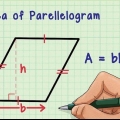
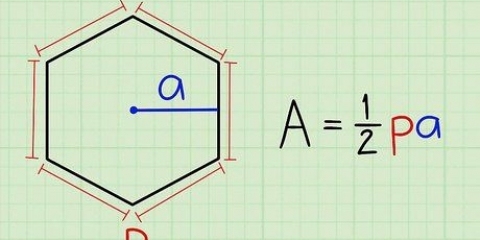
1. Skryf die formule vir die oppervlak van die vlieër. Hierdie formule werk as jy twee nie-konformerende sye ken en die grootte van die hoek tussen daardie twee sye. Die formule is  , waardeur
, waardeur  is gelyk aan die oppervlakte van die vlieër,
is gelyk aan die oppervlakte van die vlieër,  en
en  is gelyk aan die ongelyke kante van die vlieër, en
is gelyk aan die ongelyke kante van die vlieër, en  gelyk aan hoek tussen sye
gelyk aan hoek tussen sye en
en  .
.
 , waardeur
, waardeur  is gelyk aan die oppervlakte van die vlieër,
is gelyk aan die oppervlakte van die vlieër,  en
en  is gelyk aan die ongelyke kante van die vlieër, en
is gelyk aan die ongelyke kante van die vlieër, en  gelyk aan hoek tussen sye
gelyk aan hoek tussen sye en
en  .
. - Kyk of jy twee ongelyke kante het. `n Vlieër het twee pare kongruente sye. Jy moet een kant van elke paar gebruik. Maak seker jy begin by die hoek tussen hierdie twee kante. As jy nie al hierdie inligting het nie, kan jy nie hierdie metode gebruik nie.

2. Pas die lengte van die sye op die formule toe. Hierdie inligting moet gegee word, anders moet jy dit kan meet. Onthou dat jy nie-kongruente sye gebruik, so elke kant het `n ander lengte.
 .
.
3. Vermenigvuldig die kante saam. Pas hierdie produk op die formule toe.



4. Pas die hoek toe op die formule. Maak seker dat jy die hoek tussen die twee nie-kongruente sye gebruik.
 dan sal jou formule soos volg lyk:
dan sal jou formule soos volg lyk:  .
.
5. Bepaal die sinus van die hoek. Hiervoor kan jy `n sakrekenaar, of `n trigonometriese tabel gebruik.
 .
.
6. Vermenigvuldig die produk van die sye met die sinus van die hoek. Hierdie resultaat is die oppervlakte van die vlieër, in vierkante eenhede.


Die oppervlak van `n vlieër, met twee sye van 20 cm en 15 cm, en die hoek tussen hulle van 150 grade, is dus 150 vierkante cm.
Metode 3 van 3: Gebruik die area om `n ontbrekende diagonaal te vind

1. Skryf die formule vir die oppervlakte van `n vlieër, gegewe twee diagonale. Die formule is  , waardeur
, waardeur  is gelyk aan die oppervlakte van die vlieër, en
is gelyk aan die oppervlakte van die vlieër, en  en
en  gelyk aan die lengte van die vlieër se hoeklyne.
gelyk aan die lengte van die vlieër se hoeklyne.
 , waardeur
, waardeur  is gelyk aan die oppervlakte van die vlieër, en
is gelyk aan die oppervlakte van die vlieër, en  en
en  gelyk aan die lengte van die vlieër se hoeklyne.
gelyk aan die lengte van die vlieër se hoeklyne.
2. Pas die area van die vlieër op die formule toe. Hierdie inligting moet gegee word. Maak seker jy  vervang.
vervang.
 vervang.
vervang. .
.
3. pas die lengte van die bekende diagonaal op die formule toe. vervang  .
.
 .
. .
.
4. Vermenigvuldig elke kant van die vergelyking met 2. Dit sal die breuk in die formule verwyder.




5. Verdeel elke kant van die vergelyking deur die lengte van die diagonaal. Dit sal jou die lengte van die ontbrekende diagonaal gee.



Die lengte van die ontbrekende diagonaal van `n vlieër, gegewe `n oppervlakte van 35 vierkante cm en `n diagonaal van 7 cm, is dus 10 cm.
Benodigdhede
- Sakrekenaar (opsioneel)
- Liniaal (opsioneel)
- Potlood (opsioneel)
- Papier (opsioneel)
Artikels oor die onderwerp "Bereken die oppervlakte van 'n vlieër"
Оцените, пожалуйста статью
Soortgelyk
Gewilde