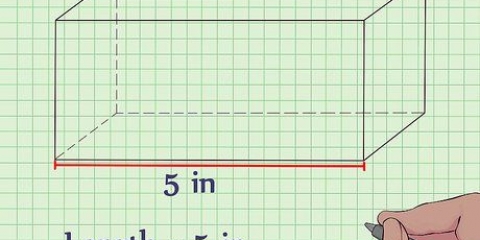
Byvoorbeeld, as die volume van die prisma 64 is  ), jou formule sal soos volg lyk:
), jou formule sal soos volg lyk:


Byvoorbeeld, as die basis `n reghoek van 8 meter lank en 2 meter breed is, sal jy die oppervlakte soos volg bereken:



Byvoorbeeld, as jy bereken het dat die oppervlakte van die basis 16 m is, sal jou formule soos volg lyk:


Byvoorbeeld, in die vergelyking  , jy moet elke kant deur 16 om deel
, jy moet elke kant deur 16 om deel  te bereken. Dus:
te bereken. Dus:


Die hoogte van die reghoekige prisma is dus 4 meter. 

Byvoorbeeld, as jy weet dat die volume van die prisma 840 kubieke meter is ( ), jou formule sal soos volg lyk:
), jou formule sal soos volg lyk:


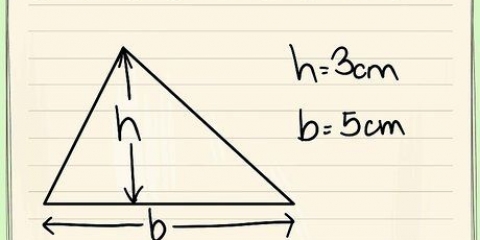
As jy die lengte van al drie sye van `n driehoek ken, kan jy die oppervlakte met behulp van Heron`s Formule bereken.lees Bereken die oppervlakte van `n driehoek vir gedetailleerde instruksies. Byvoorbeeld, as die basis van die driehoek 12 meter is, en die hoogte van die driehoek is 7 meter, vind dan die area soos volg:




Byvoorbeeld, as jy weet dat die oppervlakte van die basis 42 m2 is, sal jou formule soos volg lyk:


Byvoorbeeld, in die vergelyking  , jy moet elke kant deur 42 deel om te bepaal
, jy moet elke kant deur 42 deel om te bepaal  . Dus:
. Dus:


Dus, die hoogte van jou driehoekige prisma is 20 meter. 

Byvoorbeeld, as die area 1460 cm is, sal jou formule soos volg lyk:


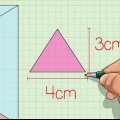
Byvoorbeeld, as die basis `n reghoek is met `n lengte van 8 cm en `n breedte van 2 cm, vind die area soos volg:



Byvoorbeeld, as die oppervlakte van die basis 16 is, sal jou formule soos volg lyk:



Onthou dat die teenoorgestelde sye van `n reghoek dieselfde lengte het. Byvoorbeeld, as die basis `n reghoek is met `n lengte van 8 cm en `n breedte van 2 cm, vind die omtrek soos volg:



Byvoorbeeld, as die omtrek van die basis 20 is, sal jou formule soos volg lyk:


Byvoorbeeld, in die vergelyking  trek eers 32 van elke kant af en deel dan elke kant deur 20. Dus:
trek eers 32 van elke kant af en deel dan elke kant deur 20. Dus:




Die hoogte van jou prisma is dus 71,4 cm. 

Byvoorbeeld, as die area 1460 cm is, sal jou formule soos volg lyk:


As jy die lengte van al drie sye van `n driehoek ken, kan jy die oppervlakte bepaal deur Heron se formule te gebruik.lees Bereken die oppervlakte van `n driehoek vir volledige instruksies. Byvoorbeeld, as die basis van die driehoek 8 cm is, en die hoogte van die driehoek is 4 cm, sal jy die oppervlakte soos volg bereken:




Byvoorbeeld, as die oppervlakte van die basis 16 is, sal jou formule soos volg lyk:



Byvoorbeeld, as die basis `n driehoek met lengtes 8, 4 en 9 cm is, bereken jy die omtrek soos volg:



Gestel byvoorbeeld die omtrek van die basis is 21, jou formule sal soos volg lyk:


Byvoorbeeld, in die vergelyking  , jy moet eers 32 van elke kant aftrek en dan elke kant deur 21 deel. Dus:
, jy moet eers 32 van elke kant aftrek en dan elke kant deur 21 deel. Dus:




Dus, die hoogte van jou prisma is 68 cm.
Bereken die hoogte van 'n prisma
Inhoud
- Trappe
- Metode 1 van 4: Bepaal die hoogte van `n reghoekige prisma met `n bekende volume
- Metode 2 van 4: Bepaling van die hoogte van `n driehoekige prisma met `n bekende volume
- Metode 3 van 4: Bepaal die hoogte van `n reghoekige prisma deur sy area te gebruik
- Metode 4 van 4: Bepaal die hoogte van `n driehoekige prisma deur sy oppervlakte te gebruik
- Benodigdhede
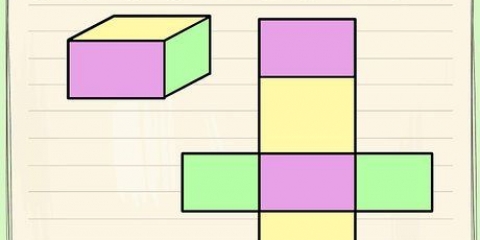
`n Prisma is `n driedimensionele figuur met twee parallelle basisse, wat kongruent is.Die vorm van die basis bepaal watter tipe prisma dit is, soos `n reghoekige of driehoekige prisma. Aangesien dit `n 3D-vorm is, is dit nie ongewoon om die volume van `n prisma te wil bereken nie; jy het egter die hoogte van die prisma daarvoor nodig. Om die hoogte te vind is moontlik wanneer jy genoeg inligting ontvang het: óf die volume, area en omtrek van die basis. Die formules wat in die onderstaande metodes beskryf word, is geskik vir prismas met basisse van enige vorm, mits jy die formule ken om die oppervlakte van daardie vorm te vind.
Trappe
Metode 1 van 4: Bepaal die hoogte van `n reghoekige prisma met `n bekende volume

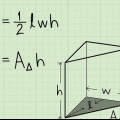
1. Gebruik die formule vir die volume van `n prisma. Die volume van `n prisma kan gevind word deur die formule te gebruik  , waardeur
, waardeur  is gelyk aan die volume van die prisma,
is gelyk aan die volume van die prisma,  is gelyk aan die oppervlakte van een basis, en
is gelyk aan die oppervlakte van een basis, en  gelyk aan die hoogte van die prisma.
gelyk aan die hoogte van die prisma.
 , waardeur
, waardeur  is gelyk aan die volume van die prisma,
is gelyk aan die volume van die prisma,  is gelyk aan die oppervlakte van een basis, en
is gelyk aan die oppervlakte van een basis, en  gelyk aan die hoogte van die prisma.
gelyk aan die hoogte van die prisma. - Die basis van `n prisma is een van sy kongruente sye. Aangesien alle teenoorstaande sye van `n reghoekige prisma kongruent is, kan enige sy as `n grondvlak gebruik word, solank jy konsekwent is met jou berekeninge.

2. Pas die volume op die formule toe. As jy nie die volume ken nie, kan jy nie hierdie metode gebruik nie.
 ), jou formule sal soos volg lyk:
), jou formule sal soos volg lyk:

3. Vind die area van die basis. Om die area te vind, moet jy die lengte en breedte van die basis ken (of van `n sy, as die basis `n vierkant is). Gebruik die formule  om die oppervlakte van `n reghoek te bepaal.
om die oppervlakte van `n reghoek te bepaal.
 om die oppervlakte van `n reghoek te bepaal.
om die oppervlakte van `n reghoek te bepaal.


4. Vervang die oppervlakte van die basis in die volume van die prismaformule. Maak seker dat jy die veranderlike vervang  .
.
 .
.

5. Los die vergelyking op vir h  . Nou weet jy die hoogte van jou prisma.
. Nou weet jy die hoogte van jou prisma.
 . Nou weet jy die hoogte van jou prisma.
. Nou weet jy die hoogte van jou prisma. , jy moet elke kant deur 16 om deel
, jy moet elke kant deur 16 om deel  te bereken. Dus:
te bereken. Dus:

Die hoogte van die reghoekige prisma is dus 4 meter.
Metode 2 van 4: Bepaling van die hoogte van `n driehoekige prisma met `n bekende volume

1. Skryf die formule neer vir die volume van `n prisma. Die volume van enige prisma kan gevind word deur die formule te gebruik  ,waardeur
,waardeur  is gelyk aan die volume van die prisma,
is gelyk aan die volume van die prisma,  is gelyk aan die oppervlakte van `n basis, en
is gelyk aan die oppervlakte van `n basis, en  gelyk aan die hoogte van die prisma.
gelyk aan die hoogte van die prisma.
 ,waardeur
,waardeur  is gelyk aan die volume van die prisma,
is gelyk aan die volume van die prisma,  is gelyk aan die oppervlakte van `n basis, en
is gelyk aan die oppervlakte van `n basis, en  gelyk aan die hoogte van die prisma.
gelyk aan die hoogte van die prisma. - Die basis van `n prisma is een van sy kongruente sye. Die basis van `n driehoekige prisma is `n driehoek. Die sye is reghoeke.

2. Pas die volume op die formule toe. As jy nie die volume ken nie, kan jy nie hierdie metode gebruik nie.
 ), jou formule sal soos volg lyk:
), jou formule sal soos volg lyk:

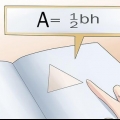
3. Vind die area van die basis. Om die area te vind, moet jy die lengte van die basis van die driehoek en die hoogte van die driehoek ken. Gebruik die formule  om die oppervlakte van `n driehoek te bepaal.
om die oppervlakte van `n driehoek te bepaal.
 om die oppervlakte van `n driehoek te bepaal.
om die oppervlakte van `n driehoek te bepaal.



4. Vervang die oppervlakte van die basis in die volume van die prismaformule. Maak seker dat jy die veranderlike vervang  .
.
 .
.

5. Los die vergelyking op vir h  . Nou weet jy die hoogte van jou prisma.
. Nou weet jy die hoogte van jou prisma.
 . Nou weet jy die hoogte van jou prisma.
. Nou weet jy die hoogte van jou prisma. , jy moet elke kant deur 42 deel om te bepaal
, jy moet elke kant deur 42 deel om te bepaal  . Dus:
. Dus:

Metode 3 van 4: Bepaal die hoogte van `n reghoekige prisma deur sy area te gebruik

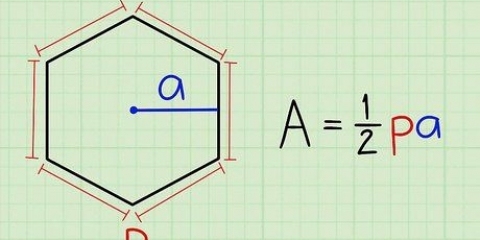
1. Skryf die formule vir die oppervlakte van `n prisma. Die formule vir die oppervlakte van `n prisma is  , waardeur
, waardeur  gelyk is aan die oppervlak,
gelyk is aan die oppervlak,  is gelyk aan die oppervlakte van die basis,
is gelyk aan die oppervlakte van die basis,  is gelyk aan die omtrek van die basis, en
is gelyk aan die omtrek van die basis, en  gelyk aan die hoogte van die prisma.
gelyk aan die hoogte van die prisma.
 , waardeur
, waardeur  gelyk is aan die oppervlak,
gelyk is aan die oppervlak,  is gelyk aan die oppervlakte van die basis,
is gelyk aan die oppervlakte van die basis,  is gelyk aan die omtrek van die basis, en
is gelyk aan die omtrek van die basis, en  gelyk aan die hoogte van die prisma.
gelyk aan die hoogte van die prisma. - Vir hierdie metode om te werk, moet jy die area van die prisma ken, sowel as die lengte en breedte van die basis.

2. Vervang die area van die prisma in die formule. As die oppervlak onbekend is, sal hierdie metode nie werk nie.


3. Vind die area van die basis. Om die area te vind, moet jy die lengte en breedte van die basis ken (of een kant, as die basis `n vierkant is). Gebruik die formule  om die oppervlakte van `n reghoek te bepaal.
om die oppervlakte van `n reghoek te bepaal.
 om die oppervlakte van `n reghoek te bepaal.
om die oppervlakte van `n reghoek te bepaal.


4. Vervang die oppervlakte van die basis in die formule vir die oppervlakte van `n prisma, en vereenvoudig. Maak seker dat jy die brief invul  .
.
 .
.


5. Bepaal die omtrek van die basis. Om die omtrek van `n reghoek te vind, tel die lengtes van al vier sye bymekaar, of vermenigvuldig die lengte van een sy met 4 as dit `n vierkant is.



6. Vervang die omtrek van die basis in die formule vir die oppervlakte van `n prisma. Maak seker dat jy die letter vervang  .
.
 .
.

7. Los die vergelyking op vir h  . Nou weet jy die hoogte van jou prisma.
. Nou weet jy die hoogte van jou prisma.
 . Nou weet jy die hoogte van jou prisma.
. Nou weet jy die hoogte van jou prisma. trek eers 32 van elke kant af en deel dan elke kant deur 20. Dus:
trek eers 32 van elke kant af en deel dan elke kant deur 20. Dus:



Metode 4 van 4: Bepaal die hoogte van `n driehoekige prisma deur sy oppervlakte te gebruik

1. Skryf die formule vir die oppervlakte van `n prisma. Die formule vir die oppervlakte van `n prisma is  , waardeur
, waardeur  gelyk is aan die oppervlak,
gelyk is aan die oppervlak,  is gelyk aan die oppervlakte van die basis,
is gelyk aan die oppervlakte van die basis,  is gelyk aan die omtrek van die basis, en
is gelyk aan die omtrek van die basis, en  gelyk aan die hoogte van die prisma.
gelyk aan die hoogte van die prisma.
 , waardeur
, waardeur  gelyk is aan die oppervlak,
gelyk is aan die oppervlak,  is gelyk aan die oppervlakte van die basis,
is gelyk aan die oppervlakte van die basis,  is gelyk aan die omtrek van die basis, en
is gelyk aan die omtrek van die basis, en  gelyk aan die hoogte van die prisma.
gelyk aan die hoogte van die prisma. - Vir hierdie metode om te werk, moet die area van die prisma bekend wees, sowel as die oppervlakte van die driehoekige basis, en die lengte van al drie sye van die basis.

2. Vervang die area van die prisma in die formule. As die oppervlak nie bekend is nie, sal hierdie metode nie werk nie.


3. Vind die area van die basis. Om die area te vind, moet jy die lengte van die basis van die driehoek en die hoogte van die driehoek ken. Gebruik die formule  om die oppervlakte van `n driehoek te bepaal.
om die oppervlakte van `n driehoek te bepaal.
 om die oppervlakte van `n driehoek te bepaal.
om die oppervlakte van `n driehoek te bepaal.



4. Vervang die oppervlakte van die basis in die formule vir die oppervlakte van `n prisma en vereenvoudig. Plaasvervanger vir  .
.
 .
.


5. Bepaal die omtrek van die basis. Om die omtrek van `n driehoek te vind, tel die lengtes van al drie sye bymekaar.



6. Vervang die omtrek van die basis in die formule vir die oppervlakte van `n prisma. Maak seker om te vervang vir  .
.
 .
.

7. Los die vergelyking op vir h  . Nou weet jy die hoogte van jou prisma.
. Nou weet jy die hoogte van jou prisma.
 . Nou weet jy die hoogte van jou prisma.
. Nou weet jy die hoogte van jou prisma. , jy moet eers 32 van elke kant aftrek en dan elke kant deur 21 deel. Dus:
, jy moet eers 32 van elke kant aftrek en dan elke kant deur 21 deel. Dus:



Benodigdhede
- Pen/potlood en papier of sakrekenaar (opsioneel)
Artikels oor die onderwerp "Bereken die hoogte van 'n prisma"
Оцените, пожалуйста статью
Soortgelyk
Gewilde