Hoe om die volume van 'n prisma te bereken

Inhoud

Trappe
Wenke

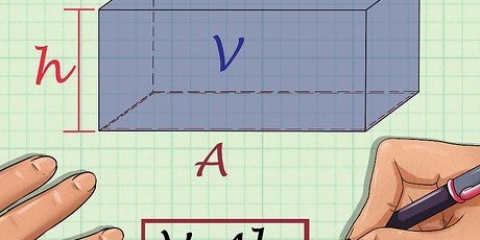
`n Prisma is `n meetkundige figuur met twee identiese punte en plat sye. Die prisma is vernoem na die vorm van sy basis, so `n prisma met `n driehoekige basis word a genoem "driehoekige prisma." Om die volume van `n prisma te bereken, al wat jy hoef te doen is om die oppervlakte van die basis te bereken en dit met die hoogte te vermenigvuldig - die berekening van die oppervlakte van die basis kan die moeilike deel wees. Hier is hoe om die volume van verskeie prismas te bereken.

Trappe

Metode 1 van 5: Bereken die volume van `n driehoekige prisma

Prent getiteld Bereken die volume van `n prisma Stap 1

1. Skryf die formule om die volume van `n driehoekige prisma te bepaal. Die formule is V = 1/2 x lengte x breedte x hoogte. Maar ons breek hierdie formule verder af om die formule te kry V = oppervlakte of basis x hoogte te gebruik. Jy kan die oppervlakte van die basis bereken deur die formule te gebruik om die oppervlakte van `n driehoek te vind - vermenigvuldig 1/2 met die lengte en breedte van die basis.

Prent getiteld Bereken die volume van `n prisma Stap 2

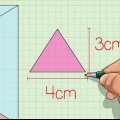
2. Bepaal die oppervlakte van die basisvlak. Om die volume van `n driehoekige prisma te vind, moet jy eers die oppervlakte van die driehoekige basis bepaal. Vind die oppervlakte van die basis van die prisma deur 1/2 keer die basis van die driehoek maal die hoogte te vermenigvuldig.

Bv: as die hoogte van die driehoekige basis 5 cm is en die basis van die driehoekige prisma 4 cm is, dan is die oppervlakte van die basis 1/2 x 5 cm x 4 cm, gelyk aan 10 cm.

Prent getiteld Bereken die volume van `n prisma Stap 3

3. Bepaal die hoogte. Gestel die hoogte van hierdie driehoekige prisma is 7 cm.

Prent getiteld Bereken die volume van `n prisma Stap 4

4. Vermenigvuldig die oppervlakte van die driehoekige basis keer die hoogte. Vermenigvuldig die oppervlakte van die basis maal die hoogte. Vermenigvuldig die basis met die hoogte, en jy kry die volume van die driehoekige prisma.

Bv: 10 cm x 7 cm = 70 cm

Prent getiteld Bereken die volume van `n prisma Stap 5

5. Gee jou antwoord in kubieke eenhede. Jy moet altyd kubieke eenhede gebruik wanneer jy `n volume bereken, want jy werk met driedimensionele voorwerpe. Die finale antwoord is 70 cm.

Metode 2 van 5: Bereken die volume van `n kubus

Prent getiteld Bereken die volume van `n prisma Stap 6

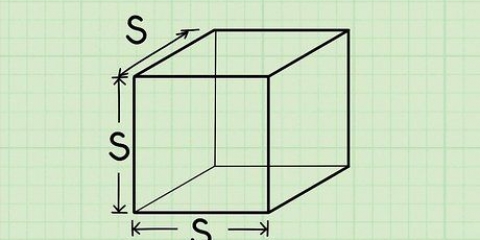
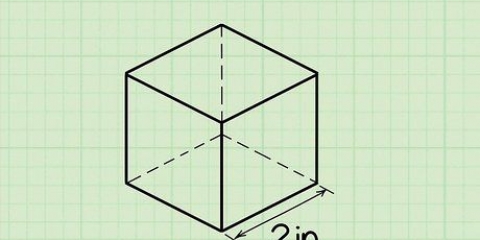
1. Skryf die formule om die volume van `n kubus te bepaal. Die formule is V = sy. `n Kubus is `n prisma met 3 gelyke sye.

Prent getiteld Bereken die volume van `n prisma Stap 7

2. Bepaal die lengte van 1 sy van die kubus. Alle kante is gelyk, so dit maak nie saak watter een jy kies nie.

Bv: Lengte = 3 cm.

Prent getiteld Bereken die volume van `n prisma Stap 8

3. Die krag van drie. Vermenigvuldig die getal met homself twee keer om die kubieke getal te kry. `n Voorbeeld is "a x a x a". Aangesien al die lengtes van die sye gelyk is, vermenigvuldig twee sye vir die oppervlakte van die basis, en `n derde sy vir die hoogte. Jy kan hieraan dink as `n vermenigvuldiging van die lengte, breedte en hoogte, wat almal dieselfde is.

Bv: 3 cm = 3 cm. * 3 cm. * 3 cm. = 27 cm.

Prent getiteld Bereken die volume van `n prisma Stap 9

4. Gee jou antwoord in kubieke eenhede.. Die finale antwoord is 27 cm.

Metode 3 van 5: Bereken die volume van `n reghoekige prisma

Prent getiteld Bereken die volume van `n prisma Stap 10

1. Skryf die formule om die volume van `n reghoekige prisma te bepaal. Die formule is V = lengte * breedte * hoogte. `n Reghoekige prisma is `n prisma met `n reghoekige basis.

Prent getiteld Bereken die volume van `n prisma Stap 11

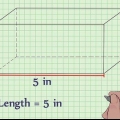
2. Bepaal die lengte. Die lengte is die langste sy van die plat oppervlak van die reghoek, bo of onder die reghoekige prisma.

Bv: Lengte = 10 cm.

Prent getiteld Bereken die volume van `n prisma Stap 12

3. Bepaal die breedte. Die breedte van die reghoekige prisma is die korter kant van die plat oppervlak van `n reghoek, aan die bo- of onderkant van die vorm.

Bv: Breedte = 8 cm.

Prent getiteld Bereken die volume van `n prisma Stap 13

4. Bepaal die hoogte. Die hoogte is daardie deel van die reghoekige prisma wat regop is. Jy kan jou die hoogte van die reghoekige prisma voorstel as daardie deel wat uit `n reghoek strek en `n driedimensionele figuur daarvan maak.

Bv: Hoogte = 5 cm.

Prent getiteld Bereken die volume van `n prisma Stap 14

5. Vermenigvuldig die lengte, breedte en hoogte. Vermenigvuldig dit in enige volgorde vir die produk. Gebruik hierdie metode om die oppervlakte van die reghoekige basis (10 x 8) en dan die volume te vind deur dit te vermenigvuldig met die hoogte, 5. Om die volume van hierdie prisma te vind, kan jy egter die lengtes van die are in enige volgorde vermenigvuldig.

Bv: 10 cm. *8 cm. * 5cm = 400cm.

Prent getiteld Bereken die volume van `n prisma Stap 15

6. Gee jou antwoord in kubieke eenhede. Die finale antwoord is 400 cm.

Metode 4 van 5: Bereken die volume van `n trapesiumvormige prisma

Prent getiteld Bereken die volume van `n prisma Stap 16

1. Skryf die formule vir die berekening van die volume van `n trapesium. Die formule is: V = [1/2 x (basis₁ + basis₂) x hoogte] x hoogte van die prisma. Gebruik die eerste deel vir die area van die basis van die prisma voordat u verder gaan.

Prent getiteld Bereken die volume van `n prisma Stap 17

2. Vind die area van die basis. Om dit te doen, voer die area van bo en onder in die formule in, saam met die hoogte.

Gestel basis 1 = 8 cm, basis 2 = 6 cm, en hoogte = 10 cm.

Bv: 1/2 x (6 + 8) x 10 = 1/2 x 14 cm x 10 cm = 80 cm.

Prent getiteld Bereken die volume van `n prisma Stap 18

3. Bepaal die hoogte van die prisma. Gestel die hoogte van die prisma is 12 cm.

Prent getiteld Bereken die volume van `n prisma Stap 19

4. Vermenigvuldig die oppervlakte van die basis maal die hoogte. Om die volume van die trapezium te bereken, vermenigvuldig die oppervlakte van die basis met die hoogte.

80cm x 12cm = 960cm.

Prent getiteld Bereken die volume van `n prisma Stap 20

5. Gee jou antwoord in kubieke eenhede. Die finale antwoord is 960 cm

Metode 5 van 5: Bereken die volume van `n gereelde vyfhoekige prisma

Prent getiteld Bereken die volume van `n prisma Stap 21

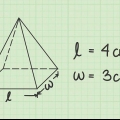
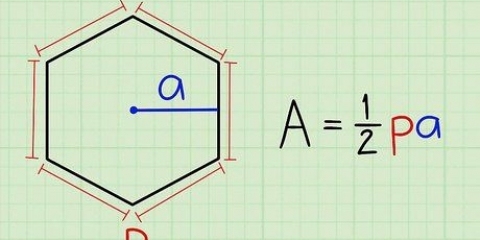
1. Skryf die formule neer om die volume van `n gereelde vyfhoekige prisma te bepaal. Die formule is V = [1/2 x 5 x sy x apotem] x hoogte van die prisma. U kan die eerste deel van die formule gebruik om die oppervlakte van die vyfhoekige basis te vind. Dink hieraan as die bepaling van die oppervlakte van die 5 driehoeke wat saam `n reëlmatige veelhoek vorm. Die sy is die breedte van 1 driehoek, en die apotem is die hoogte van een van die driehoeke.Jy vermenigvuldig nou met 1/2 want dit is deel daarvan om die oppervlakte van `n driehoek te vind en dan vermenigvuldig jy dit met 5 want daar is 5 driehoeke in `n vyfhoek.

Vir meer inligting oor die bepaling van die apotem, sien hier.

Prent getiteld Bereken die volume van `n prisma Stap 22

2. Vind die area van die vyfhoekige basis. Gestel die lengte van `n sy is 6 cm en die lengte van die apotem is 7 cm. Voer die getalle in die formule in:

A = 1/2 x 5 x sy x apotem

A = 1/2 x 5 x 6 cm x 7 cm = 105 cm

Prent getiteld Bereken die volume van `n prisma Stap 23

3. Bepaal die hoogte. Stel die hoogte van die vorm is 10 cm.

Prent getiteld Bereken die volume van `n prisma Stap 24

4. Vermenigvuldig die oppervlakte van die vyfhoekige basis keer die hoogte. Vermenigvuldig die oppervlakte van die vyfhoekige basis, 105 cm, maal die hoogte, 10 cm, om die volume van die algemene vyfhoekige prisma te vind.

105 cm x 10 cm = 1050 cm

Prent getiteld Bereken die volume van `n prisma Stap 25

5. Gee jou antwoord in kubieke eenhede. Die finale antwoord is 1050 cm.

Wenke

Probeer "basis" nie mee te verwar nie "basisvlak".`n Basisvlak verwys na die tweedimensionele vorm wat die basis van die prisma is (gewoonlik die bo- en onderkant).Maar daardie basisvlak kan sy eie basis hê --- een van die kante van die vorm van die vliegtuig, wat gebruik word om die oppervlakte van daardie vorm te vind.