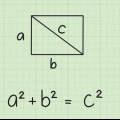
Hierdie formule is afgelei van die Pythagorese stelling ( . ’n Diagonaal verdeel ’n vierkant in twee kongruente reghoekige driehoeke, so jy kan die lengtes van die sye van die vierkant gebruik om die lengte van die diagonaal te vind (wat die skuinssy van die regte driehoek is).
. ’n Diagonaal verdeel ’n vierkant in twee kongruente reghoekige driehoeke, so jy kan die lengtes van die sye van die vierkant gebruik om die lengte van die diagonaal te vind (wat die skuinssy van die regte driehoek is). 
Byvoorbeeld, as die sye van die vierkant `n lengte van 5 sentimeter elk het, sal die formule soos volg lyk:


Byvoorbeeld, as jy die diagonaal van `n 5 sentimeter vierkant bereken, sal jou formule soos volg lyk:


Dus, die diagonaal van die vierkant is 7,07 sentimeter lank. 

Byvoorbeeld, as die omtrek van die vierkant 20 sentimeter is, sal jou formule soos volg lyk:


Byvoorbeeld:




Hierdie formule is afgelei van die Pythagorese stelling ( . ’n Diagonaal verdeel ’n vierkant in twee kongruente reghoekige driehoeke, dus kan jy die lengtes van die sye van die vierkant gebruik om die lengte van die diagonaal (die skuinssy van die regte driehoek) te bepaal.
. ’n Diagonaal verdeel ’n vierkant in twee kongruente reghoekige driehoeke, dus kan jy die lengtes van die sye van die vierkant gebruik om die lengte van die diagonaal (die skuinssy van die regte driehoek) te bepaal. 
Byvoorbeeld, as die vierkant `n lengte van 5 sentimeter het, sal die formule soos volg lyk:


Byvoorbeeld, as jy die diagonaal van `n vierkant van 5 sentimeter bereken, sal jou formule soos volg lyk:


Dus, die diagonaal van die vierkant is 7,07 sentimeter lank. 

Byvoorbeeld, as die oppervlakte van die vierkant 25 vierkante sentimeter is, sal jou formule soos volg lyk:


Byvoorbeeld:




Hierdie formule is afgelei van die Pythagorese stelling ( . ’n Diagonaal verdeel ’n vierkant in twee kongruente reghoekige driehoeke, so jy kan die lengtes van die sye van die vierkant gebruik om die lengte van die diagonaal (die skuinssy van die regte driehoek) te bepaal.
. ’n Diagonaal verdeel ’n vierkant in twee kongruente reghoekige driehoeke, so jy kan die lengtes van die sye van die vierkant gebruik om die lengte van die diagonaal (die skuinssy van die regte driehoek) te bepaal. 
Byvoorbeeld, as die vierkant `n lengte van 5 sentimeter het, sal die formule soos volg lyk:


Byvoorbeeld, as jy die diagonaal van `n vierkant van 5 sentimeter bereken, sal jou formule soos volg lyk:


Dus, die diagonaal van die vierkant is 7,07 sentimeter.
Bereken die diagonaal van 'n vierkant
Inhoud
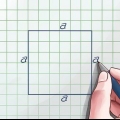
Die diagonaal van `n vierkant is die lyn van een hoek van daardie vierkant na die teenoorgestelde hoek. Gebruik die formule om die diagonaal van `n vierkant te vind 

Trappe
Metode 1 van 3: As jy die lengte van `n sy ken

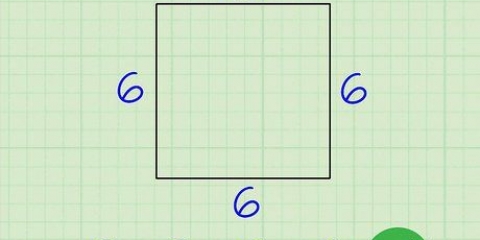
1. Vind die lengte van een sy van die vierkant. Dit is waarskynlik gegee. As jy met `n vierkant in die regte wêreld te doen het, gebruik `n liniaal of maatband om die lengte daarvan te bepaal. Aangesien al vier sye van die vierkant dieselfde lengte is, kan jy enige sy van die vierkant gebruik. As jy nie die sye van die vierkant ken nie, kan jy nie hierdie metode gebruik nie.
- Soek byvoorbeeld die lengte van die diagonaal van `n vierkant met sye van 5 sentimeter.

2. Skryf die formule neer: . In die formule is
. In die formule is  gelyk aan die lengte van die diagonaal en
gelyk aan die lengte van die diagonaal en  gelyk aan een kant van die vierkant.
gelyk aan een kant van die vierkant.
 . In die formule is
. In die formule is  gelyk aan die lengte van die diagonaal en
gelyk aan die lengte van die diagonaal en  gelyk aan een kant van die vierkant.
gelyk aan een kant van die vierkant. . ’n Diagonaal verdeel ’n vierkant in twee kongruente reghoekige driehoeke, so jy kan die lengtes van die sye van die vierkant gebruik om die lengte van die diagonaal te vind (wat die skuinssy van die regte driehoek is).
. ’n Diagonaal verdeel ’n vierkant in twee kongruente reghoekige driehoeke, so jy kan die lengtes van die sye van die vierkant gebruik om die lengte van die diagonaal te vind (wat die skuinssy van die regte driehoek is).
3. Voer die lengte van die sy van die vierkant in die formule in. Maak seker dat jy die veranderlike vervang  .
.
 .
.

4. Vermenigvuldig die lengte van die sy met 2  . Dit gee die lengte van die diagonaal. Hierdie berekening word die beste met `n sakrekenaar gedoen, sodat die antwoord meer akkuraat is. Het nie `n sakrekenaar nie, rond
. Dit gee die lengte van die diagonaal. Hierdie berekening word die beste met `n sakrekenaar gedoen, sodat die antwoord meer akkuraat is. Het nie `n sakrekenaar nie, rond  dan af na 1.414.
dan af na 1.414.
 . Dit gee die lengte van die diagonaal. Hierdie berekening word die beste met `n sakrekenaar gedoen, sodat die antwoord meer akkuraat is. Het nie `n sakrekenaar nie, rond
. Dit gee die lengte van die diagonaal. Hierdie berekening word die beste met `n sakrekenaar gedoen, sodat die antwoord meer akkuraat is. Het nie `n sakrekenaar nie, rond  dan af na 1.414.
dan af na 1.414.

Dus, die diagonaal van die vierkant is 7,07 sentimeter lank.
Metode 2 van 3: Wanneer die omtrek gegee word

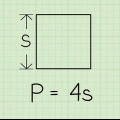
1. Skryf die formule vir die omtrek van `n vierkant. Die formule is  , waardeur
, waardeur  is gelyk aan die omtrek van die vierkant, en
is gelyk aan die omtrek van die vierkant, en  gelyk aan die lengte van een sy van die vierkant.
gelyk aan die lengte van een sy van die vierkant.
 , waardeur
, waardeur  is gelyk aan die omtrek van die vierkant, en
is gelyk aan die omtrek van die vierkant, en  gelyk aan die lengte van een sy van die vierkant.
gelyk aan die lengte van een sy van die vierkant. - Hierdie metode werk slegs as die omtrek van die vierkant gegee word.
- Om die lengte van die diagonaal te vind, moet jy eers die lengte van een sy van die vierkant vind, dus moet jy die formule vir die omtrek en
om op te los.

2. Prop die lengte van die omtrek in die formule. Maak seker dat jy die veranderlike invul  .
.
 .
.

3. Los op vir s  . Om dit te doen, deel elke kant van die vergelyking deur 4. Dit sal jou die lengte van een kant van die vierkant gee.
. Om dit te doen, deel elke kant van die vergelyking deur 4. Dit sal jou die lengte van een kant van die vierkant gee.
 . Om dit te doen, deel elke kant van die vergelyking deur 4. Dit sal jou die lengte van een kant van die vierkant gee.
. Om dit te doen, deel elke kant van die vergelyking deur 4. Dit sal jou die lengte van een kant van die vierkant gee.



4. Skryf die formule d = s 2  . In die formule is
. In die formule is  gelyk aan die lengte van die diagonaal en
gelyk aan die lengte van die diagonaal en  gelyk aan een kant van die vierkant.
gelyk aan een kant van die vierkant.
 . In die formule is
. In die formule is  gelyk aan die lengte van die diagonaal en
gelyk aan die lengte van die diagonaal en  gelyk aan een kant van die vierkant.
gelyk aan een kant van die vierkant. . ’n Diagonaal verdeel ’n vierkant in twee kongruente reghoekige driehoeke, dus kan jy die lengtes van die sye van die vierkant gebruik om die lengte van die diagonaal (die skuinssy van die regte driehoek) te bepaal.
. ’n Diagonaal verdeel ’n vierkant in twee kongruente reghoekige driehoeke, dus kan jy die lengtes van die sye van die vierkant gebruik om die lengte van die diagonaal (die skuinssy van die regte driehoek) te bepaal.
5. Prop die lengte van die sy van die vierkant in die formule. Maak seker dat jy die veranderlike vervang  .
.
 .
.

6. Vermenigvuldig die lengte van die sy met 2  . Dit sal jou die lengte van die diagonaal gee. Dit is die beste om hierdie berekening met `n sakrekenaar te doen, om `n meer akkurate resultaat te kry. As jy nie `n sakrekenaar het nie, rond af
. Dit sal jou die lengte van die diagonaal gee. Dit is die beste om hierdie berekening met `n sakrekenaar te doen, om `n meer akkurate resultaat te kry. As jy nie `n sakrekenaar het nie, rond af  af teen 1,414.
af teen 1,414.
 . Dit sal jou die lengte van die diagonaal gee. Dit is die beste om hierdie berekening met `n sakrekenaar te doen, om `n meer akkurate resultaat te kry. As jy nie `n sakrekenaar het nie, rond af
. Dit sal jou die lengte van die diagonaal gee. Dit is die beste om hierdie berekening met `n sakrekenaar te doen, om `n meer akkurate resultaat te kry. As jy nie `n sakrekenaar het nie, rond af  af teen 1,414.
af teen 1,414.

Dus, die diagonaal van die vierkant is 7,07 sentimeter lank.
Metode 3 van 3: Wanneer die area gegee word

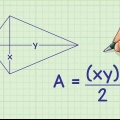
1. Skryf die formule vir die oppervlakte van `n vierkant. Die formule is  , waardeur
, waardeur  is gelyk aan die oppervlakte van die vierkant, en
is gelyk aan die oppervlakte van die vierkant, en  gelyk aan die lengte van een sy van die vierkant.
gelyk aan die lengte van een sy van die vierkant.
 , waardeur
, waardeur  is gelyk aan die oppervlakte van die vierkant, en
is gelyk aan die oppervlakte van die vierkant, en  gelyk aan die lengte van een sy van die vierkant.
gelyk aan die lengte van een sy van die vierkant. - Hierdie metode werk slegs as die oppervlakte van die vierkant bekend is.
- Om die lengte van die diagonaal te vind, moet jy eers die lengte van een sy van die vierkant bepaal, die rede hoekom jy eers die oppervlakteformule moet gebruik, en
om op te los.

2. Vervang die waarde vir die area in die formule. Maak seker dat jy die veranderlike vervang  .
.
 .
.

3. Los op vir s  . Jy doen dit deur die vierkantswortel van die area te bepaal. Dit sal jou die lengte van een kant van die vierkant gee. Bepaal nou die vierkantswortel met `n sakrekenaar. As jy hulp nodig het om die vierkantswortel met die hand te bereken, lees Bereken die vierkantswortel van `n getal sonder `n sakrekenaar.
. Jy doen dit deur die vierkantswortel van die area te bepaal. Dit sal jou die lengte van een kant van die vierkant gee. Bepaal nou die vierkantswortel met `n sakrekenaar. As jy hulp nodig het om die vierkantswortel met die hand te bereken, lees Bereken die vierkantswortel van `n getal sonder `n sakrekenaar.
 . Jy doen dit deur die vierkantswortel van die area te bepaal. Dit sal jou die lengte van een kant van die vierkant gee. Bepaal nou die vierkantswortel met `n sakrekenaar. As jy hulp nodig het om die vierkantswortel met die hand te bereken, lees Bereken die vierkantswortel van `n getal sonder `n sakrekenaar.
. Jy doen dit deur die vierkantswortel van die area te bepaal. Dit sal jou die lengte van een kant van die vierkant gee. Bepaal nou die vierkantswortel met `n sakrekenaar. As jy hulp nodig het om die vierkantswortel met die hand te bereken, lees Bereken die vierkantswortel van `n getal sonder `n sakrekenaar.



4. Skryf die formule d = s 2  . In die formule is
. In die formule is  gelyk aan die lengte van die diagonaal en is
gelyk aan die lengte van die diagonaal en is  gelyk aan een kant van die vierkant.
gelyk aan een kant van die vierkant.
 . In die formule is
. In die formule is  gelyk aan die lengte van die diagonaal en is
gelyk aan die lengte van die diagonaal en is  gelyk aan een kant van die vierkant.
gelyk aan een kant van die vierkant. . ’n Diagonaal verdeel ’n vierkant in twee kongruente reghoekige driehoeke, so jy kan die lengtes van die sye van die vierkant gebruik om die lengte van die diagonaal (die skuinssy van die regte driehoek) te bepaal.
. ’n Diagonaal verdeel ’n vierkant in twee kongruente reghoekige driehoeke, so jy kan die lengtes van die sye van die vierkant gebruik om die lengte van die diagonaal (die skuinssy van die regte driehoek) te bepaal.
5. Gebruik die lengte van die sy van die vierkant in die formule. Maak seker dat jy die veranderlike vervang  .
.
 .
.

6. Vermenigvuldig die lengte van die sy met 2  . Dit sal jou die lengte van die diagonaal gee. Dit is die beste om hierdie berekening met `n sakrekenaar te doen, om `n meer akkurate resultaat te kry. As jy nie `n sakrekenaar het nie, rond af
. Dit sal jou die lengte van die diagonaal gee. Dit is die beste om hierdie berekening met `n sakrekenaar te doen, om `n meer akkurate resultaat te kry. As jy nie `n sakrekenaar het nie, rond af  af teen 1,414.
af teen 1,414.
 . Dit sal jou die lengte van die diagonaal gee. Dit is die beste om hierdie berekening met `n sakrekenaar te doen, om `n meer akkurate resultaat te kry. As jy nie `n sakrekenaar het nie, rond af
. Dit sal jou die lengte van die diagonaal gee. Dit is die beste om hierdie berekening met `n sakrekenaar te doen, om `n meer akkurate resultaat te kry. As jy nie `n sakrekenaar het nie, rond af  af teen 1,414.
af teen 1,414.

Dus, die diagonaal van die vierkant is 7,07 sentimeter.
Benodigdhede
- Sakrekenaar
Artikels oor die onderwerp "Bereken die diagonaal van 'n vierkant"
Оцените, пожалуйста статью
Soortgelyk
Gewilde