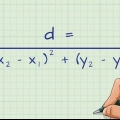Byvoorbeeld, as die breedte van `n reghoek 3 cm is en die lengte is 4 cm, sal jou formule soos volg lyk:  .
. 
Byvoorbeeld:




Byvoorbeeld:



Dus, die diagonaal of `n reghoek met `n breedte van 3 cm en `n lengte van 4 cm is 5 cm. 

Byvoorbeeld, as die oppervlakte van die reghoek 35 vierkante sentimeter is, sal jou formule soos volg lyk:  .
. 
Byvoorbeeld:

 .
. 

Byvoorbeeld, as die omtrek van `n reghoek 24 sentimeter is, sal jou formule soos volg lyk:  .
. 
Byvoorbeeld:


 .
. 
Byvoorbeeld, as jy met die area formule gevind het dat  , dan vervang jy die waarde
, dan vervang jy die waarde  in die omtreksformule:
in die omtreksformule:



Byvoorbeeld:




Byvoorbeeld:




Byvoorbeeld,  word
word  .
. 
Byvoorbeeld, die vergelyking  kan opgelos word in
kan opgelos word in  .
. 
Byvoorbeeld:


EN

 .
.
Dus, die lengte en breedte van die reghoek is 7 cm en 5 cm. 
Jy gebruik die Pythagoras-stelling omdat die diagonaal van `n reghoek dit in twee kongruente reghoekige driehoeke verdeel. Die breedte en lengte van die reghoek is die lengtes van die sye van die driehoek; die diagonaal is die skuinssy van die driehoek. 
Byvoorbeeld, as jy weet dat die breedte en lengte van die reghoek 5 cm en 7 cm is, sal jou formule soos volg lyk:  .
. 
Byvoorbeeld:




Byvoorbeeld:



Dus is die diagonaal van `n reghoek met `n oppervlakte van 35 cm en `n omtrek van 24 cm ongeveer 8,6 cm. 

Jy kan hierdie metode gebruik as jy die omtrek van die reghoek ken, behalwe dat jy nou die omtrekformule gebruik in plaas van die oppervlakteformule. Die formule vir die omtrek van `n reghoek is  , waardeur
, waardeur  is gelyk aan die breedte van die reghoek, en
is gelyk aan die breedte van die reghoek, en  is gelyk aan die lengte van die reghoek.
is gelyk aan die lengte van die reghoek. 
Byvoorbeeld, as die oppervlakte van die reghoek 35 vierkante sentimeter is, sal jou formule soos volt lyk:  .
. 
Byvoorbeeld, as jy dit gevind het  , dan vervang jy hierdie verhouding vir
, dan vervang jy hierdie verhouding vir  in die area formule:
in die area formule:



Byvoorbeeld:




Byvoorbeeld, die vergelyking  kan ontbind word as
kan ontbind word as  .
. 
Byvoorbeeld:


EN

 .
.
In hierdie geval is daar een negatiewe antwoord. Aangesien die lengte van `n reghoek nie negatief kan wees nie, weet jy dat die lengte 5 cm moet wees. 
Byvoorbeeld, as jy weet dat die lengte van die reghoek 5 cm is, en dat die verhouding tussen die lengtes van die sye  , dan voer jy 5 as lengte in die formule in:
, dan voer jy 5 as lengte in die formule in:




Jy gebruik die Pythagoras-stelling omdat die diagonaal van `n reghoek dit in twee kongruente reghoekige driehoeke verdeel. Die breedte en lengte van die reghoek is die lengtes van die sye van die driehoek; die diagonaal is die skuinssy van die driehoek. 
Byvoorbeeld, as jy weet dat die breedte en lengte van die reghoek gelyk is aan 5 cm en 7 cm, lyk jou formule nou so:  .
. 
Byvoorbeeld:




Byvoorbeeld:



Dus is die diagonaal van `n reghoek met `n breedte wat 2 cm meer is as sy lengte, en het `n oppervlakte van 35 cm, ongeveer 8,6 cm.
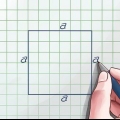
Bereken die lengte van die diagonaal in 'n reghoek
Inhoud
`n Diagonaal is `n reguit lyn wat een hoek van `n reghoek met die teenoorgestelde hoek verbind. ’n Reghoek het twee hoeklyne, elk van dieselfde lengte. As jy die lengtes van die sye van `n reghoek ken, is dit maklik om die lengte van die diagonaal te vind deur die Pythagoras-stelling te gebruik, want `n diagonaal verdeel `n reghoek in twee reghoekige driehoeke. As jy nie die lengtes van die sye ken nie, maar jy het wel ander data (soos die oppervlakte en die omtrek, of die verhouding tussen die lengtes van die sye), kan jy die lengte en breedte van die sye meet met `n paar ekstra stappe. vind die reghoek, en gebruik dan die Pythagoras-stelling, vind die lengte en breedte van die diagonaal.
Trappe
Metode 1 van 3: Gebruik die lengte en breedte

1. Skryf die formule vir die Pythagoras-stelling neer. Die formule is  , waardeur
, waardeur  en
en  is gelyk aan die lengtes van die sye van `n reghoekige driehoek, en
is gelyk aan die lengtes van die sye van `n reghoekige driehoek, en  is gelyk aan die lengte van die skuinssy van `n reghoekige driehoek.
is gelyk aan die lengte van die skuinssy van `n reghoekige driehoek.
 , waardeur
, waardeur  en
en  is gelyk aan die lengtes van die sye van `n reghoekige driehoek, en
is gelyk aan die lengtes van die sye van `n reghoekige driehoek, en  is gelyk aan die lengte van die skuinssy van `n reghoekige driehoek.
is gelyk aan die lengte van die skuinssy van `n reghoekige driehoek. - Jy gebruik die Pythagoras-stelling omdat die diagonaal van `n reghoek dit in twee kongruente reghoekige driehoeke verdeel. Die lengte en breedte van die reghoek is die lengtes van die sye van die driehoek; die diagonaal is die skuinssy van die driehoek.

2. Pas die lengte en breedte op die formule toe. Dit is as dit korrek gegee is, of jy kan dit meet. Maak seker om te vervang vir  en
en  .
.
 en
en  .
. .
.
3. Kwadra die lengte en die breedte en tel dan hierdie getalle bymekaar. Kwadratering is om die getal met homself te vermenigvuldig.




4. Trek die vierkantswortel van elke kant van die vergelyking af. Die maklikste manier om `n vierkantswortel te vind, is om `n sakrekenaar te gebruik. Jy kan `n aanlyn sakrekenaar gebruik as jy nie `n wetenskaplike sakrekenaar het nie. Dit gee jou die waarde  , of die skuinssy van die driehoek en die diagonaal van die reghoek.
, of die skuinssy van die driehoek en die diagonaal van die reghoek.
 , of die skuinssy van die driehoek en die diagonaal van die reghoek.
, of die skuinssy van die driehoek en die diagonaal van die reghoek.


Dus, die diagonaal of `n reghoek met `n breedte van 3 cm en `n lengte van 4 cm is 5 cm.
Metode 2 van 3: Gebruik die area en omtrek

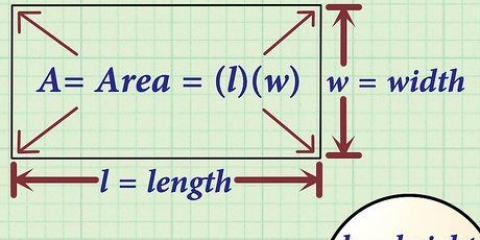
1. Skryf die formule vir die oppervlakte van `n reghoek. Die formule is  , waardeur
, waardeur  is gelyk aan die oppervlakte van die reghoek,
is gelyk aan die oppervlakte van die reghoek,  is gelyk aan die lengte van die reghoek, en
is gelyk aan die lengte van die reghoek, en  gelyk aan die breedte van die reghoek.
gelyk aan die breedte van die reghoek.
 , waardeur
, waardeur  is gelyk aan die oppervlakte van die reghoek,
is gelyk aan die oppervlakte van die reghoek,  is gelyk aan die lengte van die reghoek, en
is gelyk aan die lengte van die reghoek, en  gelyk aan die breedte van die reghoek.
gelyk aan die breedte van die reghoek.
2. Gebruik die oppervlakte van die reghoek in die formule. Maak seker dat jy die korrekte veranderlike vervang  .
.
 .
. .
.
3. Herrangskik die formule, en jy kry `n waarde vir w  . Jy doen dit deur beide kante van die vergelyking te deel deur
. Jy doen dit deur beide kante van die vergelyking te deel deur  . Sit hierdie waarde opsy. Jy sal dit later in die formule vir die omtrek gebruik.
. Sit hierdie waarde opsy. Jy sal dit later in die formule vir die omtrek gebruik.
 . Jy doen dit deur beide kante van die vergelyking te deel deur
. Jy doen dit deur beide kante van die vergelyking te deel deur  . Sit hierdie waarde opsy. Jy sal dit later in die formule vir die omtrek gebruik.
. Sit hierdie waarde opsy. Jy sal dit later in die formule vir die omtrek gebruik.
 .
.
4. Skryf die formule vir die omtrek van `n reghoek. Die formule is  , waardeur
, waardeur  is gelyk aan die breedte van die reghoek, en
is gelyk aan die breedte van die reghoek, en  is gelyk aan die lengte van die reghoek.
is gelyk aan die lengte van die reghoek.
 , waardeur
, waardeur  is gelyk aan die breedte van die reghoek, en
is gelyk aan die breedte van die reghoek, en  is gelyk aan die lengte van die reghoek.
is gelyk aan die lengte van die reghoek.
5. Gebruik die waarde van die omtrek in die formule. Maak seker dat jy die veranderlike vervang  .
.
 .
. .
.
6. Deel beide kante van die vergelyking deur 2. Dit gee jou die waarde  .
.
 .
.

 .
.
7. Gebruik die waarde w  in die vergelyking. Gebruik die waarde wat jy gevind het deur die oppervlakteformule te herrangskik.
in die vergelyking. Gebruik die waarde wat jy gevind het deur die oppervlakteformule te herrangskik.
 in die vergelyking. Gebruik die waarde wat jy gevind het deur die oppervlakteformule te herrangskik.
in die vergelyking. Gebruik die waarde wat jy gevind het deur die oppervlakteformule te herrangskik. , dan vervang jy die waarde
, dan vervang jy die waarde  in die omtreksformule:
in die omtreksformule:


8. Elimineer die breuk in die vergelyking. Jy doen dit deur beide kante van die vergelyking te vermenigvuldig met  .
.
 .
.



9. Stel die vergelyking gelyk aan 0. Jy doen dit deur die eerstegraadse term van beide kante van die vergelyking af te trek.




10. Herrangskik die volgorde van die terme in die vergelyking. Dit beteken dat die term met die eksponent eerste kom, gevolg deur die term met die veranderlike, en uiteindelik die konstante. Wanneer u herrangskik, let op die korrekte positiewe en negatiewe tekens. Die vergelyking is nou as kwadratiese vergelyking georden.
 word
word  .
.
11. Faktoreer die kwadratiese vergelyking. Lees die artikel vir gedetailleerde instruksies oor hoe om dit te doen Los kwadratiese vergelykings op.
 kan opgelos word in
kan opgelos word in  .
.
12. Bepaal die waardes van l  . Jy doen dit deur elke term op nul te stel en vir die veranderlike op te los. Jy kry twee oplossings vir hierdie vergelyking. Aangesien jy met `n reghoek te doen het, sal die twee oplossings die breedte en lengte van jou reghoek wees.
. Jy doen dit deur elke term op nul te stel en vir die veranderlike op te los. Jy kry twee oplossings vir hierdie vergelyking. Aangesien jy met `n reghoek te doen het, sal die twee oplossings die breedte en lengte van jou reghoek wees.
 . Jy doen dit deur elke term op nul te stel en vir die veranderlike op te los. Jy kry twee oplossings vir hierdie vergelyking. Aangesien jy met `n reghoek te doen het, sal die twee oplossings die breedte en lengte van jou reghoek wees.
. Jy doen dit deur elke term op nul te stel en vir die veranderlike op te los. Jy kry twee oplossings vir hierdie vergelyking. Aangesien jy met `n reghoek te doen het, sal die twee oplossings die breedte en lengte van jou reghoek wees.

EN

 .
.Dus, die lengte en breedte van die reghoek is 7 cm en 5 cm.

13. Skryf die formule vir die Pythagoras-stelling neer. Die formule is  , waardeur
, waardeur  en
en  is gelyk aan die lengtes van die sye van `n reghoekige driehoek, en
is gelyk aan die lengtes van die sye van `n reghoekige driehoek, en  is gelyk aan die lengte van die skuinssy van `n reghoekige driehoek.
is gelyk aan die lengte van die skuinssy van `n reghoekige driehoek.
 , waardeur
, waardeur  en
en  is gelyk aan die lengtes van die sye van `n reghoekige driehoek, en
is gelyk aan die lengtes van die sye van `n reghoekige driehoek, en  is gelyk aan die lengte van die skuinssy van `n reghoekige driehoek.
is gelyk aan die lengte van die skuinssy van `n reghoekige driehoek.
14. Gebruik die breedte- en lengtegraad in die formule. Dit maak nie saak watter waarde jy vir watter veranderlike gebruik nie.
 .
.
15. Kwadra die breedte- en lengtegraad en tel dan hierdie getalle bymekaar. Om te kwadraat beteken om `n getal met homself te vermenigvuldig.




16. Neem die vierkantswortel van elke kant van die vergelyking. Die maklikste manier om `n vierkantswortel te vind, is deur `n sakrekenaar te gebruik. Jy kan `n aanlyn sakrekenaar gebruik as jy nie `n wetenskaplike sakrekenaar het nie. Dit gee jou die waarde  , en dit is die skuinssy van die driehoek, en die diagonaal van die reghoek.
, en dit is die skuinssy van die driehoek, en die diagonaal van die reghoek.
 , en dit is die skuinssy van die driehoek, en die diagonaal van die reghoek.
, en dit is die skuinssy van die driehoek, en die diagonaal van die reghoek.


Dus is die diagonaal van `n reghoek met `n oppervlakte van 35 cm en `n omtrek van 24 cm ongeveer 8,6 cm.
Metode 3 van 3: Gebruik die oppervlakte en verhoudingslengtes van die sye

1. Skryf `n formule wat die verband tussen die lengtes van die sye verduidelik. Jy kan die lengte verander ( ) of die breedte (
) of die breedte ( ) isoleer. Sit hierdie formule vir `n oomblik opsy. Jy sal dit binnekort in die oppervlakformule gebruik.
) isoleer. Sit hierdie formule vir `n oomblik opsy. Jy sal dit binnekort in die oppervlakformule gebruik.
 ) of die breedte (
) of die breedte ( ) isoleer. Sit hierdie formule vir `n oomblik opsy. Jy sal dit binnekort in die oppervlakformule gebruik.
) isoleer. Sit hierdie formule vir `n oomblik opsy. Jy sal dit binnekort in die oppervlakformule gebruik. - Byvoorbeeld, as jy weet dat die breedte van `n reghoek 2 cm meer as sy lengte is, kan jy `n formule soos
:
.

2. Skryf die formule vir die oppervlakte van `n reghoek. Die formule is  , waardeur
, waardeur  is gelyk aan die oppervlakte van die reghoek,
is gelyk aan die oppervlakte van die reghoek,  is gelyk aan die lengte van die reghoek, en
is gelyk aan die lengte van die reghoek, en  gelyk aan die breedte van die reghoek.
gelyk aan die breedte van die reghoek.
 , waardeur
, waardeur  is gelyk aan die oppervlakte van die reghoek,
is gelyk aan die oppervlakte van die reghoek,  is gelyk aan die lengte van die reghoek, en
is gelyk aan die lengte van die reghoek, en  gelyk aan die breedte van die reghoek.
gelyk aan die breedte van die reghoek. , waardeur
, waardeur  is gelyk aan die breedte van die reghoek, en
is gelyk aan die breedte van die reghoek, en  is gelyk aan die lengte van die reghoek.
is gelyk aan die lengte van die reghoek.
3. Gebruik die oppervlakte van die reghoek in die formule. Maak seker dat jy die veranderlike vervang  .
.
 .
. .
.
4. Gebruik die verhoudingsformule vir die lengte (of breedte) in die formule. Aangesien jy met `n reghoek te doen het, maak dit nie saak of jy met veranderlike werk nie  of
of  .
.
 of
of  .
. , dan vervang jy hierdie verhouding vir
, dan vervang jy hierdie verhouding vir  in die area formule:
in die area formule:


5. Maak dit `n kwadratiese vergelyking. Jy doen dit deur die distributiewe eienskap te gebruik en die terme tussen hakies met mekaar te vermenigvuldig, waarna jy die vergelyking gelyk stel aan 0.




6. Faktoreer die kwadratiese vergelyking. Lees die artikel vir gedetailleerde instruksies oor hoe om dit te doen Los kwadratiese vergelykings op.
 kan ontbind word as
kan ontbind word as  .
.
7. Bepaal die waardes van l  . Jy doen dit deur elke term gelyk aan nul te maak en die veranderlike op te los. Jy kry twee oplossings vir die vergelyking.
. Jy doen dit deur elke term gelyk aan nul te maak en die veranderlike op te los. Jy kry twee oplossings vir die vergelyking.
 . Jy doen dit deur elke term gelyk aan nul te maak en die veranderlike op te los. Jy kry twee oplossings vir die vergelyking.
. Jy doen dit deur elke term gelyk aan nul te maak en die veranderlike op te los. Jy kry twee oplossings vir die vergelyking.

EN

 .
.In hierdie geval is daar een negatiewe antwoord. Aangesien die lengte van `n reghoek nie negatief kan wees nie, weet jy dat die lengte 5 cm moet wees.

8. Gebruik die waarde van die lengte (of breedte) in jou verhoudingsformule. Dit sal jou die lengte van die ander kant van die reghoek gee.
 , dan voer jy 5 as lengte in die formule in:
, dan voer jy 5 as lengte in die formule in:



9. Skryf die formule vir die Pythagoras-stelling neer. Die formule is  , waardeur
, waardeur  en
en  is gelyk aan die lengtes van die sye van `n reghoekige driehoek, en
is gelyk aan die lengtes van die sye van `n reghoekige driehoek, en  is gelyk aan die lengte van die skuinssy van `n reghoekige driehoek.
is gelyk aan die lengte van die skuinssy van `n reghoekige driehoek.
 , waardeur
, waardeur  en
en  is gelyk aan die lengtes van die sye van `n reghoekige driehoek, en
is gelyk aan die lengtes van die sye van `n reghoekige driehoek, en  is gelyk aan die lengte van die skuinssy van `n reghoekige driehoek.
is gelyk aan die lengte van die skuinssy van `n reghoekige driehoek.
10. Gebruik die breedte- en lengtegraad in die formule. Dit maak nie saak watter waarde jy vir watter veranderlike gebruik nie.
 .
.
11. Kwadra die breedte- en lengtegraad en tel dan hierdie getalle bymekaar. Om te kwadraat beteken om `n getal met homself te vermenigvuldig.




12. Trek die vierkantswortel van elke kant van die vergelyking af. Die maklikste manier om `n vierkantswortel te vind, is deur `n sakrekenaar te gebruik. Jy kan `n aanlyn sakrekenaar gebruik as jy nie `n wetenskaplike sakrekenaar het nie. Dit gee jou die waarde  , of die skuinssy van die driehoek en dus die diagonaal van die reghoek.
, of die skuinssy van die driehoek en dus die diagonaal van die reghoek.
 , of die skuinssy van die driehoek en dus die diagonaal van die reghoek.
, of die skuinssy van die driehoek en dus die diagonaal van die reghoek.


Dus is die diagonaal van `n reghoek met `n breedte wat 2 cm meer is as sy lengte, en het `n oppervlakte van 35 cm, ongeveer 8,6 cm.
Artikels oor die onderwerp "Bereken die lengte van die diagonaal in 'n reghoek"
Оцените, пожалуйста статью
Soortgelyk
Gewilde