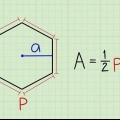
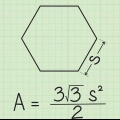
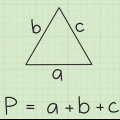Hoe om die omtrek van 'n veelhoek te bereken

Inhoud

Trappe

`n Veelhoek is enige tweedimensionele vorm wat reguit lyne het. Daar is beide reëlmatige veelhoeke (dié met gelyke sye) en onreëlmatige veelhoeke (dié met verskillende sylengtes). Die metodes om die omtrek van gereelde en onreëlmatige veelhoeke te vind is `n bietjie anders, maar albei is maklik sodra jy weet wat om te doen. Jy kan ook sy omtrek op `n koördinaatrooster vind. As jy probeer om die omtrek van `n gereelde veelhoek te vind, gebruik die formule: omtrek = aantal sye x die lengte van elke sy.

Trappe

Metode 1 van 3: Vind die omtrek van `n gereelde veelhoek

Prent getiteld Vind die omtrek van `n veelhoek Stap 1

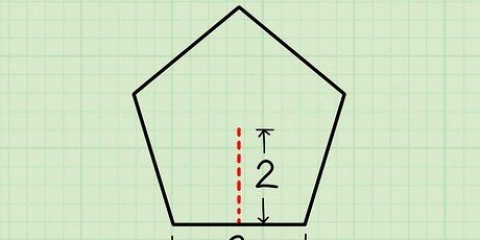
1. Kyk of die sye van die veelhoek almal ewe lank is. Gereelde veelhoeke is veelhoeke met gelyke sye. As die sye van die veelhoek waarna jy kyk nie almal ewe lank is nie, moet jy die omtrek vind deur die onreëlmatige veelhoek metode te gebruik. As die sye ewe lank is, het jy te doen met `n gereelde veelhoek.

Wenk: As sommige sye nie gemerk is nie, kyk na die res van die veelhoek om die lengtes te bepaal. Byvoorbeeld, as jy `n vierkant het waarvan net een sy `n gegewe lengte het, dan weet jy dat die ander sye dieselfde lengte het, want vierkante het gelyke sye.

Prent getiteld Vind die omtrek van `n veelhoek Stap 2

2. Skryf die lengte van een sy van die veelhoek neer. Dit maak nie saak watter kant jy kies nie, want alle sylengtes is dieselfde. Maak net seker dat jy net die lengte van een van die sye neerskryf.

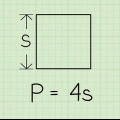
Gestel jy het byvoorbeeld te doen met `n vierkant met `n sylengte van ses, jy sal `6` skryf.

Prent getiteld Vind die omtrek van `n veelhoek Stap 3

3. Skryf die totale aantal sye wat die veelhoek het neer. Moenie bekommerd wees oor die lengte van die sye op hierdie punt nie. Tel net hoeveel sye die veelhoek het en skryf dit neer.

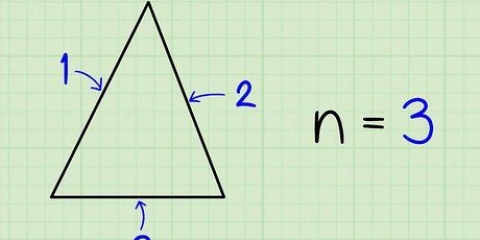
Vir `n vierkant skryf jy `4` want `n vierkant het vier sye.

Prent getiteld Vind die omtrek van `n veelhoek Stap 4

4. Vermenigvuldig die lengte van die sy met die aantal sye om die omtrek te kry. Die formule om die omtrek van `n gereelde veelhoek te vind is eenvoudig die aantal sye maal die lengte van enige sy. As jy daardie twee getalle saam vermenigvuldig het, het jy die omtrek van die veelhoek gevind!

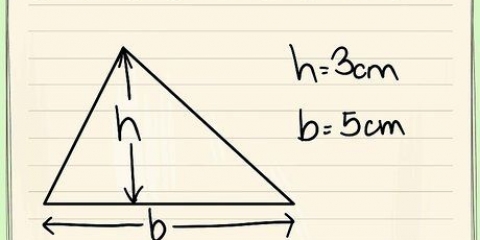
In die voorbeeld met die vierkant weet jy dat die vierkant `n sylengte van ses en `n totaal van vier sye het. Daarom kan jy net omtrek van die vierkant met 6 x 4 = 24 bereken.

Of veronderstel jy het te doen met `n driehoek met `n sylengte van drie. Aangesien `n driehoek drie sye het, sal jy 3 (die aantal sye) x 3 (die sylengte) = 9 doen. Die omtrek van die driehoek is dus 9.

Metode 2 van 3: Bereken die omtrek van `n onreëlmatige veelhoek

Prent getiteld Vind die omtrek van `n veelhoek Stap 5

1. Bepaal uit die lengte van die veelhoek of dit onreëlmatig is. `n Onreëlmatige veelhoek is `n veelhoek met geen gelyke sye nie. As die sye van die veelhoek almal ewe lank is, beteken dit dat die veelhoek reëlmatig is, nie onreëlmatig nie.

Het jy geweet? Jy kan dieselfde metode gebruik om die omtrek van `n onreëlmatige veelhoek te vind om die omtrek van `n gereelde veelhoek te vind, maar nie andersom.

Prent getiteld Vind die omtrek van `n veelhoek Stap 6

2. Skryf die lengte van elke sy van die veelhoek neer. Aangesien nie alle sye van `n onreëlmatige veelhoek gelyk is nie, moet jy elke individuele sy neerskryf. Selfs as sommige sye gelyk is, moet jy steeds elke lengte afsonderlik neerskryf.

Byvoorbeeld, as jy `n reghoek het met twee sye lengte 4 en twee sye lengte 3, kan jy skryf: `4, 4, 3, 3`.

As jy met `n onreëlmatige veelhoek met `n sy van 2, `n sy van 3 en `n sy van 4 eenhede lank werk, kan jy skryf: `2, 3, 4`.

Prent getiteld Vind die omtrek van `n veelhoek Stap 7

3. Voeg al die lengtes bymekaar om die omtrek te vind. Om die omtrek van `n onreëlmatige veelhoek te vind, hoef jy net die som van alle sye te vind. Tel net die lengte van elke sy wat jy neergeskryf het by om die omtrek van die veelhoek te vind!

Byvoorbeeld, as die sylengtes vir die veelhoek 4, 4, 3 en 3 was, dan is die som gelyk aan 14. Daarom is 14 die omtrek van die veelhoek.

Metode 3 van 3: Bepaal die omtrek deur gegewe koördinate te gebruik

Prent getiteld Vind die omtrek van `n veelhoek Stap 8

1. Teken `n koördinaatstelsel met `n x- en y-as. `n Koördinaatstelsel is `n grafiek met `n x- en y-asse waarop jy koördinate kan aandui. Om `n koördinaatstelsel te teken, neem `n vel grafiekpapier of teken jou eie roosterlyne op `n leë stuk papier met `n liniaal. Trek dan `n horisontale lyn deur die middel van die x-as en `n vertikale lyn deur die middel vir die y-as. Nommer laastens die punte op elke as, begin met `0` waar die x-as en y-as sny.

Wanneer jy die koördinaatstelsel nommer, sal die getalle bo en regs van die 0 positief wees, terwyl die getalle onder en links van die 0 negatief sal wees.

Prent getiteld Vind die omtrek van `n veelhoek Stap 9

2. Dui die gegewe koördinate op die grafiek aan. Jy moes koördinate gegee het vir elke hoekpunt van die veelhoek wie se omtrek jy probeer vind. Elke koördinaat moet soos `(1,2)` lyk. Gebruik die nommers wat jy op die koördinaatstelsel gemerk het om elk van die koördinate aan te dui. Wanneer jy klaar is, verbind daardie punte met reguit lyne om die vorm van die veelhoek waarmee jy werk, te sien.

Wenk: Wanneer jy die koördinate spesifiseer, onthou dat die eerste getal die x-as verteenwoordig en die tweede getal die y-as verteenwoordig. Byvoorbeeld, as jy sê (2.4), gaan jy na 2 op die x-as en van daar af na 4 op die y-as en merk daardie punt in die rooster.

Prent getiteld Vind die omtrek van `n veelhoek Stap 10

3. Vind vertikale en horisontale lengtes van sye deur die eenhede te tel. Jy moet die lengte van elke sy van die veelhoek ken om sy omtrek te bepaal. Vir vertikale of horisontale sye, tel net hoeveel eenhede daar tussen die kolletjies aan elke kant is. Skryf dan die nommer langs daardie kant neer sodat jy later daarna kan verwys.

Byvoorbeeld, as jy die lengte van `n horisontale sy probeer vind, begin by die een kant en tel die aantal vierkante tussen daardie punt en die ander kant. As jy ses tel, sal dit beteken dat die lengte van daardie sy 6 eenhede is.

Prent getiteld Vind die omtrek van `n veelhoek Stap 11

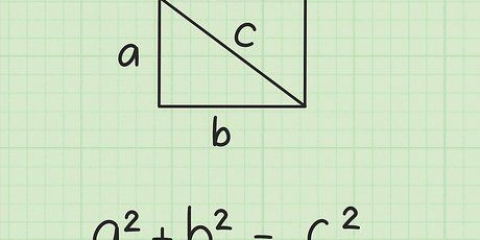
4.Gebruik die afstandsformule om die lengte van diagonale sye te vind. Ongelukkig kan jy nie die eenhede op `n rooster tel om die lengte van die diagonale sye te vind soos jy kan met vertikale of horisontale sye nie (aangesien jy met heelgetalle te doen het). Jy kan eerder die afstandformule gebruik:

d = \sqrt{(X} 2 - X_{1})^{2} + (y_{2} - y_{1})^{2}

$d={sqrt{(x_{{2}}-x_{{1}})^{{2}}+(y_{{2}}-y_{{1}})^{{2}}} }$ . Voer net die waardes van die x- en y-koördinate in vir die twee punte aan die einde van die kant wat jy probeer vind en los die formule op om die lengte te vind.

As jy byvoorbeeld die afstand (lengte) tussen twee punte met koördinate (4.7) en (1.3) probeer vind, sal jy daardie koördinate in die formule gebruik en kry:

d = \sqrt{(4} 2 - 1_{1})^{2} + (7_{2} - 3_{1})^{2}

${displaystyle d={sqrt {(4_{2}-1_{1})^{2}+(7_{2}-3_{1})^{2}}}}$

Dan kan jy die vergelyking vereenvoudig en kry:

d = \sqrt{25}

$d={sqrt{25}}$ .

Uiteindelik laat jy gaan

d = \sqrt{25}

$d={sqrt{25}}$ aan en jy kry 5 as antwoord. Die lengte van die sy is dus 5.

Prent getiteld Vind die omtrek van `n veelhoek Stap 12

5. Tel die lengte van elke sy bymekaar om die omtrek van die veelhoek te vind. Die omtrek van `n veelhoek is gelyk aan die som van alle sylengtes. Sodra jy al hierdie lengtes bepaal het deur gebruik te maak van die koördinate wat jy gegee het, al wat jy hoef te doen is om hulle bymekaar te tel en jy is klaar!

Byvoorbeeld, as jy die koördinate van `n driehoek geplot het en jy vind dat die sylengtes 3, 2 en 5 is, dan tel jy hierdie getalle bymekaar om 10 te kry. Die omtrek van die driehoek is dus 10.