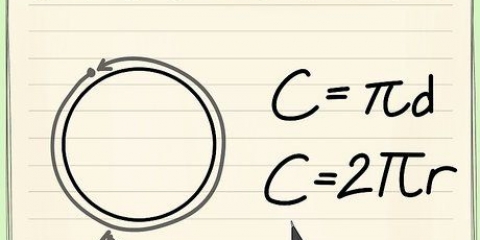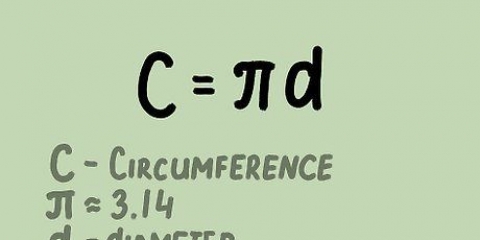Kom ons sê die oppervlakte van die sirkel is 500 cm. Dan werk jy die vergelyking soos volg uit: 2√3.14 x 500. 
As die berekening gelyk is aan 2√3.14 x 500, dan bereken jy eers 3.14 x 500 = 1570. Bereken dan 2√1,570. 
Die vierkantswortel van 1570 is 39,6. 
Bereken 39,6 x 2 = 79,2. Dit beteken dat die omtrek 79,2 cm is, wat die formule oplos. 

Gestel die oppervlakte van die sirkel is 200 cm. Die vergelyking word dan 200 = 3,14 x R. 
As jy 200 deur 3,14 deel, is die resultaat 63,7. Die nuwe vergelyking is dus 63.7 = R. 
Die vierkantswortel van 63.7 is 7.9. Die vergelyking word dan 7.9 = R, wat beteken dat die radius van die sirkel 7.9 is. Dit sal jou al die inligting gee wat jy nodig het om die omtrek te vind. 
Gebruik die eerste opsie, 7,9 x 2 = 15,8, die deursnee van die sirkel. Hierdie deursnee keer 3,14 is 49,6. Vir die tweede opsie word die berekening 2 x 3,14 x 7,9. Eers bereken jy 2 x 3,14 = 6,28, en dit vermenigvuldig met 7,9 is 49,6. Let op hoe albei metodes jou dieselfde antwoord gee.
Bereken omtrek deur area te gebruik
Inhoud
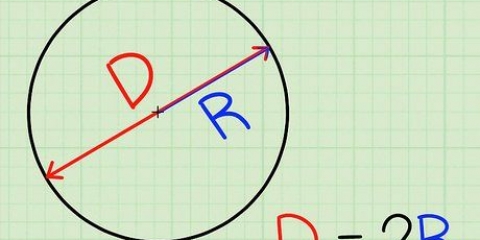
Die formule vir die berekening van die omtrek (C) van `n sirkel, C = πD of C = 2πR, is eenvoudig as jy die sirkel se deursnee (D) of radius (R) ken. Maar wat doen jy as jy net die area van die sirkel ken? Soos baie dinge in wiskunde is daar verskeie oplossings vir hierdie probleem. Die formule C = 2√πA is ontwerp om die omtrek van `n sirkel te vind deur gebruik te maak van die area (A). Jy kan ook die vergelyking A = πR omkeer om R te vind, en dan R in die omtreksvergelyking invoer. Beide vergelykings gee dieselfde resultaat.
Trappe
Metode 1 van 2: Gebruik die omtrekvergelyking

1. Gebruik die formule C=2√πA om die probleem op te los. Hierdie formule bereken die omtrek van `n sirkel as jy net sy oppervlakte ken. C staan vir die omtrek en A vir die area. Skryf hierdie formule om die probleem te begin oplos.
- Die π-simbool, wat vir pi staan, is `n herhalende desimale met (nou) duisende syfers na die desimale punt. Vir eenvoud, gebruik 3.14 as die waarde van pi.
- Aangesien jy in elk geval pi na sy numeriese vorm moet omskakel, gebruik 3.14 van die begin af in die vergelyking. Skryf dit as C = 2√3.14 x A.

2. Sluit die area as A by die vergelyking in. Aangesien jy reeds die oppervlakte van die sirkel ken, is dit die waarde van A. Gaan dan voort om die probleem op te los deur die volgorde van bewerkings te gebruik.

3. Vermenigvuldig pi met die oppervlakte van die sirkel. In die volgorde van bewerkings kom die bewerkings binne die vierkantswortelsimbool eerste. Vermenigvuldig pi met die oppervlakte van die sirkel wat jy ingeprop het. Sluit dan die resultaat by die vergelyking in.

4. Besondervierkantswortel van die som. Daar is verskeie maniere om die vierkantswortel te bereken. As jy `n sakrekenaar gebruik, druk die funksie √ en tik die getal in. Jy kan ook die probleem met die hand oplos deur priemfaktore te gebruik.

5. Vermenigvuldig die vierkantswortel met 2 om die omtrek te vind. Ten slotte voltooi jy die berekening deur die resultaat met 2 te vermenigvuldig. Dit gee `n finale getal terug, die omtrek.
Metode 2 van 2: Los die probleem omgekeerd op

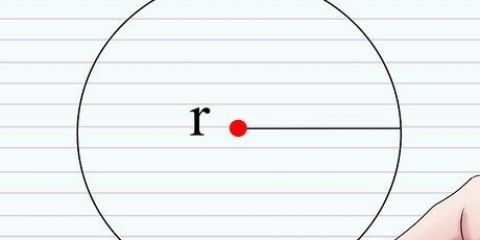
1. Gebruik die formule A = πR in. Dit is die formule vir die oppervlakte van `n sirkel. A staan vir die area en R vir die radius. Normaalweg sal jy dit gebruik as jy die radius ken, maar jy kan ook die area invul om die vergelyking op te los.
- Weereens, gebruik 3.14 as die afgeronde waarde vir pi.

2. Voer die area as waarde vir A in. Gebruik die oppervlakte van die sirkel in die vergelyking. Plaas dit aan die linkerkant van die vergelyking as die waarde vir A.

3. Deel beide kante van die vergelyking deur 3.14. Om hierdie soort vergelyking op te los, moet jy die stappe aan die regterkant geleidelik uitskakel deur die teenoorgestelde bewerkings te doen. Aangesien jy die waarde van pi ken, deel jy elke kant deur daardie waarde. Dit skakel pi aan die regterkant uit en gee jou `n nuwe numeriese waarde aan die linkerkant.

4. Besondervierkantswortel van die resultaat om die radius van die sirkel te kry. Dan word die eksponent aan die regterkant van die vergelyking uitgeskakel. Die teenoorgestelde van `eksponensiëring` is om die vierkantswortel van die getal te vind. Vind die vierkantswortel van elke sy van die vergelyking. Dit verwyder die eksponent aan die regterkant en plaas die radius aan die linkerkant.

5.Bepaal die omtrek van die sirkel deur die radius te gebruik. Daar is twee formules om die omtrek (C) te vind. Die eerste is C = πD, waar D die deursnee is. Vermenigvuldig die radius met 2 om die deursnee te vind. Die tweede is C = 2πR. Vermenigvuldig 3,14 met 2 en vermenigvuldig dan die resultaat met die radius. Beide formules sal jou dieselfde resultaat gee.
Artikels oor die onderwerp "Bereken omtrek deur area te gebruik"
Оцените, пожалуйста статью
Soortgelyk
Gewilde