Bereken pi

Inhoud

Trappe
Wenke

Pi (π) is een van die belangrikste en mees fassinerende getalle in wiskunde. Eenvoudig vertoon as 3.14, word gebruik as `n konstante vir die berekening van die omtrek van `n sirkel, deur die radius of deursnee daarvan te gebruik. Dit is ook `n irrasionale getal, wat beteken dat jy dit tot `n oneindige aantal desimale plekke kan bereken sonder om ooit `n herhalende patroon teë te kom. Dit maak dit moeilik, maar nie onmoontlik nie, om akkuraat te werk.

Trappe

Metode 1 van 5: Bereken Pi deur `n sirkel te gebruik

1. Maak seker dat jy `n perfekte sirkel gebruik. Hierdie metode sal nie werk met `n ellips, ellips of enigiets anders as `n regte sirkel nie. `n Sirkel word gedefinieer as alle punte in `n vlak wat ewe ver van `n gegewe sentrale punt is. Byvoorbeeld, deksels van `n konfytfles is `n lekker hulpmiddel om vir hierdie oefening te gebruik. Jy kan rofweg `n waarde van Pi hiermee bereken. Selfs die dunste, skerpste potlood is steeds enorm in vergelyking met die akkuraatheid wat nodig is vir `n presiese berekening van die getal Pi.

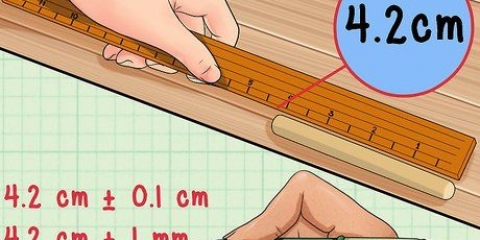
2. Meet die omtrek van die sirkel so akkuraat as wat jy kan. Die omtrek is die lengte van die hele omtrek van die sirkel. Aangesien dit rondgaan, kan dit `n bietjie moeilik wees om te meet (dit is hoekom Pi so belangrik is).

Lê `n draad om die omtrek, so presies as moontlik. Merk die draad wanneer die sirkel voltooi is, meet dan die lengte van die draad met `n liniaal.

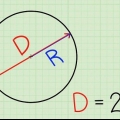
3. Meet die deursnee van die sirkel. Die deursnee is die lengte van die dwarssnit van `n sirkel deur die middel van die sirkel.

4. Gebruik die formule. Die omtrek van `n sirkel kan met die formule gevind word C=π*d=2*π*r. Dus pi is gelyk aan die omtrek van die sirkel gedeel deur die deursnee. Tik jou getalle in `n sakrekenaar: die resultaat moet ongeveer 3 wees.moet 14 wees.

5. Vir `n meer akkurate resultaat, herhaal hierdie proses vir verskeie sirkels, en dan `n gemiddelde van die resultate. Jou lesings is dalk nie perfek as dit by `n individuele lesing kom nie, maar met verloop van tyd behoort die gemiddelde `n baie goeie benadering van Pi te wees.

Metode 2 van 5: Bereken Pi met behulp van Oneindige Reeks

1. Maak gebruik van die Gregory-Leibniz-reeks. Wiskundiges het verskeie wiskundige rye gevind wat, as dit tot oneindig gevolg word, Pi tot `n enorme aantal desimale plekke kan bereken. Sommige van hierdie rye is so kompleks dat dit superrekenaars verg om dit te verwerk. Een van die eenvoudigste is egter die Gregory-Leibniz-reeks. Miskien nie baie doeltreffend nie, maar dit produseer `n meer akkurate getal vir pi met elke iterasie, en eindig uiteindelik op 5 desimale plekke na 500.000 herhalings. Hier is die formule om te gebruik.

π=(4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15) ...
Neem 4 en trek 4 gedeel deur 3 hiervan af. Tel dan 4 by gedeel deur 5. Trek dan weer 4 af gedeel deur 7. Hou aan om hierdie patroon te herhaal met `n teller 4 en `n opeenvolgende onewe getal in die noemer. Hoe meer jy dit doen, hoe nader kom jy aan pi.

2. Maak gebruik van die Nilakantha-reekse. Dit is nog `n oneindige reeks wat jou toelaat om pi te bereken en is nie moeilik om te verstaan nie. Alhoewel `n bietjie meer ingewikkeld, kan jy pi baie vinniger daarmee bereken as met die Leibniz-formule.

π=3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11) *12) - 4/(12*13*14) ...

Jy pas hierdie formule toe deur eers 2 te neem en dan om die beurt breuke op te tel en af te trek, met die teller 4 en die noemer die produk van 3 opeenvolgende heelgetalle wat met elke nuwe iterasie toeneem. Elke opeenvolgende breuk begin met `n reeks heelgetalle waar die eerste getal van die reeks die laaste getal van die vorige reeks is (in die vorige breuk). Al doen jy dit net `n paar keer, sal jy gou naby pi kom.

Metode 3 van 5: Bereken Pi deur Buffon se Naaldprobleem te gebruik

1. Probeer die volgende eksperiment om pi te bereken deur worsbroodjies te gooi. Pi verskyn ook in die gedagte-eksperiment genaamd Buffon`s Needle Problem, wat probeer om die waarskynlikheid te bepaal dat willekeurig gegooide, soortgelyke-vormige voorwerpe tussen of op `n reeks parallelle lyne op die vloer sal land. Dit blyk dat as die afstand tussen die lyne gelyk is aan die lengte van die gegooi voorwerpe, dan kan die aantal kere wat die voorwerpe op `n lyn land na baie gooie gebruik word om pi te bereken.

Wetenskaplikes en wiskundiges het nog nie `n manier ontdek om pi presies te bereken nie, want hulle het nog nie `n materiaal gevind wat so dun is dat jy presiese berekeninge daarmee kan doen nie.

Metode 4 van 5: Bereken Pi met `n limiet

1. Kies `n groot aantal. Hoe groter die getal, hoe meer akkuraat sal jou berekening wees.

2. Gebruik die getal, wat ons x sal noem, in hierdie formule om pi te bereken:x *sonde (180 / x). Om dit te laat werk, maak seker dat jou sakrekenaar op grade gestel is. Die rede waarom dit `n limiet genoem word, is dat die resultaat daarvan `beperk` is tot pi. Soos jy jou getal x verhoog, kom die resultaat nader en nader aan die waarde van pi.

Metode 5 van 5: Arcsinus en Inverse Sinus Funksie

1. Kies `n getal tussen -1 en 1. Dit is omdat die boogsinus nie gedefinieer is vir getalle groter as 1 of minder as -1 nie.

2. Gebruik die getal in die volgende formule en die resultaat is ongeveer gelyk aan pi.

pi=2 *(Arcsin(sqrt(1 - x^2))) + abs(Arcsin(x)).

Arcsin verwys na `n omgekeerde sinus in radiale

Sqrt is `n afkorting vir die vierkantswortel van

Abs is `n afkorting vir absolute waarde

x^2 is `n sekere mag, in hierdie geval x kwadraat.

Wenke

Om pi te bereken is pret en uitdagend, maar as jy te veel desimale plekke bereken, sal dit nie baie nuttig wees nie .Sterrekundiges sê dit neem nie meer as 39 desimale plekke vir die getal pi om hoogs akkurate berekeninge te doen nie.