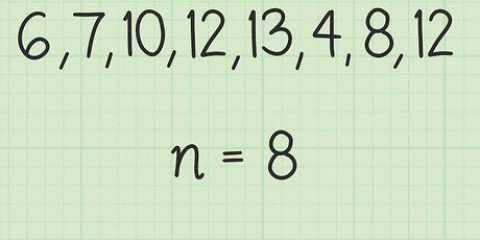Bereken onakkuraatheid

Inhoud

Trappe
Wenke
Waarskuwings

Wanneer jy `n meting neem terwyl jy data insamel, kan jy aanvaar dat daar `n "werklike waarde" is binne die omvang van die metings wat jy gemaak het. As jy die onakkuraatheid van jou lesings wil bereken, moet jy die beste skatting van jou lesing vind en dit in ag neem wanneer jy die onakkuraatheid van die lesing aftrek of bytel.

Trappe

Metode 1 van 3: Leer die basiese beginsels

Prent getiteld Bereken onsekerheid Stap 1

1. Bepaal die korrekte vorm vir onakkuraatheid. Gestel jy meet die lengte van `n stok van ongeveer 4,2 cm, met `n marge van 1 millimeter. Dit beteken dat die stok amper seker 4,2 cm is, maar effens groter of kleiner as hierdie lengte kan wees, met `n foutmarge van 1 millimeter.

Teken dit soos volg aan: 4,2 cm ± 0,1 cm. Jy kan dit herskryf as: 4,2 cm ± 1 mm, want 0,1 cm = 1 mm.

Prent getiteld Bereken onsekerheid Stap 2

2. Rond die eksperimentele lesing af tot dieselfde aantal desimale plekke as die onakkuraatheid. Metings wat onakkuraatheid behels, word gewoonlik tot 1 of 2 beduidende syfers afgerond. Die sleutelpunt is dat jy die eksperiment se metings tot dieselfde aantal desimale plekke as die onakkuraatheid afrond om die metings konsekwent te hou.

As die eksperimentele meting 60 cm is, sal die berekening van die onakkuraatheid ook tot `n heelgetal afgerond moet word. Byvoorbeeld, die onakkuraatheid van hierdie meting kan 60 cm ± 2 cm wees, maar nie 60 cm ± 2 nie.2 cm.

As jou eksperimentele lesing gelyk is aan 3.4 cm, dan sal die onakkuraatheid ook tot 0,1 cm afgerond moet word. Byvoorbeeld, die onakkuraatheid van hierdie meting kan 3 wees.4 cm ± .wees 1 cm, maar nie 3 nie.4 cm ± 1 cm.

Prent getiteld Bereken onsekerheid Stap 3

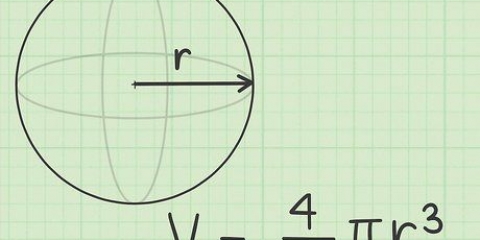
3. Bereken die onakkuraatheid van `n enkele meting. Gestel jy meet die deursnee van `n ronde bal met `n liniaal. Dit is moeilik, want dit is moeilik om presies vas te stel waar die buitenste rand van die bal is en hoe om dit met die liniaal te meet. Gestel die liniaal kan die deursnee met `n akkuraatheid van 0,1 cm vind - dit beteken nie dat jy die deursnee van die bal tot daardie vlak van akkuraatheid kan meet nie.

Kyk mooi na die rand van die bal en die liniaal om `n idee te kry van hoe betroubaar jou meting kan wees. In `n standaardliniaal is die 0,5 cm-merke duidelik gemerk - maar gestel jy kan `n bietjie nader as dit kom. As dit lyk of jy binne 0,3 cm kan kom met jou meting, dan is die onakkuraatheid 0,3 cm.

Nou gaan ons die deursnee van die bal meet. Gestel jy kry 7.6 cm as `n antwoord. Skryf nou die beraamde meting met die onakkuraatheid neer. Die deursnee van die bal is 7,6 cm ± 0,3 cm.

Prent getiteld Bereken onsekerheid Stap 4

4. Bereken die onakkuraatheid van `n enkele meting van veelvuldige voorwerpe. Gestel jy meet die hoogte van `n stapel van 10 CD-houers wat almal afmetings het. Gestel jy wil weet wat die dikte van 1 boks is. Hierdie lesing is so klein dat die persentasie onakkuraatheid aan die hoë kant sal wees. Maar as jy 10 bokse meet, kan jy die resultaat verdeel en net die onakkuraatheid daarvan deel deur die aantal bokse in die stapel om die dikte van 1 boks te vind.

Gestel jy kan nie veel nader as 0,2 cm met `n gewone liniaal kom nie. Dus, die onakkuraatheid is ± 0,2 cm.

Gestel jy het gemeet dat die stapel bokse saam 22 cm is.

Al wat jy nou hoef te doen is om hierdie metingswaarde en die onakkuraatheid te deel deur 10 (die aantal bokse). 22 cm/10 = 2,2 cm en 0,2 cm/10 = 0,02 cm. Dit beteken dat die dikte van 1 boks gelyk is aan 2,20 cm ± 0,02 cm.

Prent getiteld Bereken onsekerheid Stap 5

5. Voer hierdie meting verskeie kere uit. Om die akkuraatheid van jou meting te verhoog, of jy nou die lengte van `n voorwerp meet, of die hoeveelheid tyd wat dit geneem het om `n sekere afstand af te lê, sal jy die kanse op `n akkurate lesing verhoog as jy veelvuldige metings neem. Die bepaling van die gemiddelde van alle metings sal uiteindelik lei tot `n beter bepaling van die onakkuraatheid van `n meting.

Metode 2 van 3: Bereken die onakkuraatheid van veelvuldige metings

Prent getiteld Bereken onsekerheid Stap 6

1. Neem verskeie metings. Gestel jy wil bereken hoe lank dit neem vir `n bal om van die tafel af op die rondte te val. Vir die beste resultate sal jy ten minste `n paar keer dieselfde meting moet uitvoer – kom ons sê ons doen dit vyf keer. Dan sal jy die gemiddelde van hierdie 5 metings moet bereken en dan die standaardafwyking hiervan bytel of aftrek, vir die beste resultaat.

Gestel jy het die volgende lesings: 0,43 s, 0,52 s, 0,35 s, 0,29 s en 0,49 s.

Prent getiteld Bereken onsekerheid Stap 7

2. Bepaal die gemiddelde van die metings. Jy doen dit deur al vyf van hulle bymekaar te tel en die som te deel deur 5, die aantal gemete waardes. 0,43 s + 0,52 s + 0,35 s + 0,29 s + 0,49 s = 2.08 s. Deel nou 2.08 by 5. 2.08/5 = 0.42 sek. Die gemiddelde is 0,42 s.

Prent getiteld Bereken onsekerheid Stap 8

3. Bepaal die variansie van hierdie metings. Jy doen dit deur die verskil tussen elk van die 5 metings en die gemiddelde te bepaal. Trek die lesings van 0.42 s af. Hier is die 5 verskille:

0,43 s – 0,42 s = 0,01 s

0.52s - 0.42s = 0.1s

0.35 s - 0.42 s = -0.07 s

0.29 s - 0.42 s = -0.13 s

0,49 s - 0,42 s = 0,07 s

Tel nou die vierkante van die verskille by: (0.01 s) + (0.1 s) + (-0.07 s) + (-0.13 s) +(0.07 s)= 0.037 s.

Vind die gemiddelde van hierdie bygevoegde vierkante deur die resultaat deur 5 te deel. 0,037 s/5 = 0,0074 s.

Prent getiteld Bereken onsekerheid Stap 9

4. Bepaal die standaardafwyking. Dit kan gevind word deur die vierkantswortel van die variansie te bereken. Die kwadraat van 0,0074 s = 0,09 s, dus die standaardafwyking is 0,09 s.

Prent getiteld Bereken onsekerheid Stap 10

5. Gee die finale gemete waarde. Jy doen dit deur die gemiddelde van die gemete waardes saam met die opgetelde en afgetrekte standaardafwyking op te let. Aangesien die gemiddelde van die lesings 0,42 s is en die standaardafwyking 0,09 s, is die finale lesing 0,42 s ± 0,09 s.

Metode 3 van 3: Rekenkundige bewerkings met onakkuraatheid

Prent getiteld Bereken onsekerheid Stap 11

1. Voeg onakkuraatheid by. Jy doen dit deur die lesings bymekaar te tel en hul onakkuraathede by te voeg:

(5 cm ± .2cm) + (3cm ± .1 cm) =
(5cm + 3cm) ± (.2 cm +. 1 cm) =
8 cm ± .3 cm

Prent getiteld Bereken onsekerheid Stap 12

2. Onakkuraatheid aftrek. Jy doen dit deur die gemete waardes af te trek en die onakkuraathede by te tel:

(10 cm ± .4 cm) - (3 cm ± .2 cm) =

(10 cm - 3 cm) ± (.4 cm +. 2 cm) =

7cm ± 0,6cm

3. Vermenigvuldiging van onakkuraatheid.
Om onakkuraatheid te vermenigvuldig, vermenigvuldig die metings en tel die RELATIEWE onakkuraatheid by (as `n persentasie):
Die berekening van onakkuraathede deur vermenigvuldiging werk nie met absolute waardes nie (soos met optel en aftrek), maar wel met relatiewe waardes. Jy kry die relatiewe onakkuraatheid deur die absolute onakkuraatheid deur die gemete waarde te deel en dit dan met 100 te vermenigvuldig.
Byvoorbeeld:

(6 cm ± 0.2 cm) = (0.2 / 6) x 100 en voeg `n %-teken daarby. Dit is 3,3%
Dus:

(6 cm ± 0.2 cm) x (4 cm ± 0.3 cm) = (6 cm ± 3.3% ) x (4 cm ± 7.5%)

(6 cm x 4 cm) ± (3.3 + 7,5) =

24 cm ± 10.8% = 24 cm ± 2.6 cm

4. Deel onakkuraatheid.
Om onakkuraatheid te verdeel, verdeel die metings en voeg die RELATIEWE onakkuraatheid by:
Hierdie prosedure is gelykstaande aan `n vermenigvuldiging!

(10 cm ± 0.6 cm) ÷ (5 cm ± 0.2 cm) = (10 cm ± 6%) ÷ (5 cm ± 4%)

(10 cm ÷ 5 cm) ± (6% + 4%) =

2cm ± 10% = 2cm ± 0.2cm

Prent getiteld Bereken onsekerheid Stap 15

5. Verhoog `n onakkurate lees eksponensieel. Om `n onakkurate meting eksponensieel te verhoog, verhoog die meting met `n sekere mag, en vermenigvuldig dan die onakkuraatheid met daardie mag:

(2,0 cm ± 1.0 cm) =

(2,0 cm) ± (1,0 cm) x 3 =

8.0cm ± 3cm

Wenke

Jy kan resultate en die verstek onakkuraatheid as `n geheel bekyk, of vir elke resultaat binne `n stel data. `n Algemene reël is dat data wat uit veelvuldige metings verkry word, minder akkuraat is as wat direk van `n individuele meting verkry word.

Waarskuwings

Onakkuraatheid soos hier beskryf is slegs van toepassing op die gevalle waar normale (Gaussiese, klokvormige) statistieke gebruik word. Ander verspreidings vereis `n ander metode om onakkuraatheid te beskryf.
Goeie navorsing hou nooit op nie "feite" of wat "waar" is. Alhoewel `n meting baie waarskynlik binne `n sekere reeks onakkuraatheid sal val, is daar geen waarborg dat dit sal wees nie. Dit is inherent aan wetenskaplike gemete waardes dat daar `n moontlikheid is dat gemete waardes verkeerd is.