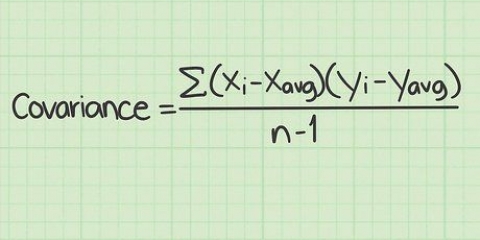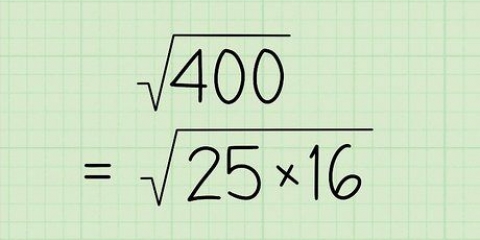Die gemiddelde is die gemiddelde waarde van alle getalle. Jy bereken die gemiddelde deur al die getalle in jou steekproef bymekaar te tel en dan hierdie waarde te deel deur die aantal getalle in jou steekproef (n). Die toetsgraaddatastel (10, 8, 10, 8, 8 en 4) bestaan uit 6 nommers. Geldig dus: n = 6. 
Gebruik byvoorbeeld die toetsgraaddatastel: 10, 8, 10, 8, 8 en 4. 10 + 8 + 10 + 8 + 8 + 4 = 48. Dit is die som van alle getalle in die datastel of steekproef. Voeg die nommers `n tweede keer by om die antwoord na te gaan. 
Die toetsgraaddatastel (10, 8, 10, 8, 8 en 4) bestaan uit ses getalle. Geldig dus: n = 6. Die som van al die toetsgrade in die voorbeeld was 48. Jy moet dus 48 deur n deel om die gemiddelde te bereken. 48/6 = 8 Die gemiddelde toetsgraad in die steekproef is 8. 

Byvoorbeeld, in ons steekproef van toetsgrade (10, 8, 10, 8, 8 en 4), was die gemiddelde of rekenkundige gemiddelde 8. 10 - 8 = 2; 8 - 8 = 0.10 - 8 = 2.8 - 8 = 0.8 - 8 = 0 en 4 - 8 = -4. Herhaal die berekeninge weer om elke antwoord na te gaan. Dit is baie belangrik dat alle getalle korrek is, want jy sal dit nodig hê vir die volgende stap. 
Onthou hoe ons in ons steekproef die gemiddelde (8) van elk van die getalle in die steekproef (10, 8, 10, 8, 8 en 4) afgetrek het en ons het die volgende resultate gekry: 2, 0, 2, 0 , 0 en -4. In die volgende berekening om die variansie te bepaal, doen die volgende: 2, 0, 2, 0, 0 en (-4) = 4, 0, 4, 0, 0 en 16. Kontroleer asseblief jou antwoorde voordat jy aangaan na die volgende stap. 
In ons toetsgraadvoorbeeld het ons die volgende vierkante bereken: 4, 0, 4, 0, 0 en 16. Onthou dat ons in die voorbeeld met toetsgrade begin het deur die gemiddelde van elk van die getalle af te trek en dan die resultate te kwadraeer: (10-8) + (8-8) + (10-2) + (8- 8) + ( 8-8) + (4-8) 4 + 0 + 4 + 0 + 0 + 16 = 24. Die som van die vierkante is 24. 
Ons voorbeeld van toetsgrade (10, 8, 10, 8, 8 en 4) bestaan uit 6 syfers. Geldig dus: n = 6. n - 1 = 5. Die som van vierkante vir hierdie steekproef was 24. 24/5 = 4,8. Die variansie van hierdie steekproef is dus 4,8. 

Tipies is ten minste 68% van alle waardes binne een standaardafwyking van die gemiddelde. Onthou, in ons steekproef van toetsgrade was die afwyking 4,8. √4.8 = 2.19. Die standaardafwyking van ons steekproef van toetsgrade is dus 2,19. 5 uit 6 getalle (83%) in ons steekproef van toetsgrade (10, 8, 10, 8, 8 en 4) is binne een standaardafwyking (2.19) van die gemiddelde (8). 
Dit is belangrik dat jy al die stappe uitskryf wanneer jy die berekeninge uit die kop of met `n sakrekenaar doen. As jy die tweede keer `n ander resultaat kry, gaan jou berekening na. As jy nie jou fout kan vind nie, begin oor `n derde keer om jou berekeninge te vergelyk.
Bereken standaardafwyking
Inhoud
Die standaardafwyking vertel jou wat die verspreiding van die getalle in jou steekproef is. Om die standaardafwyking vir jou steekproef of datastel te vind, moet jy eers `n paar berekeninge doen. Jy moet die gemiddelde en variansie van jou data bepaal voordat jy die standaardafwyking kan bereken. Die variansie is `n maatstaf van die verspreiding van jou waardes rondom die gemiddelde. Die standaardafwyking word bepaal deur die vierkantswortel van die variansie te bereken.Hierdie artikel vertel jou hoe om die gemiddelde, variansie en standaardafwyking te bereken.
Trappe
Metode 1 van 3: Bereken die gemiddelde

1. Kyk na jou dataversameling. Dit is `n belangrike stap in enige statistiese berekening, selfs `n eenvoudige waarde soos die gemiddelde of mediaan.
- Weet hoeveel getalle jou monster bevat.
- Is die getalle ver uitmekaar?? Of is die verskille tussen die getalle klein, byvoorbeeld slegs `n paar desimale plekke?
- Weet na watter tipe data jy kyk. Wat beteken die getalle in jou steekproef? Dit kan byvoorbeeld toetsgrade, hartklopwaardes, lengte, gewig, ensovoorts wees.
- Byvoorbeeld, `n toetsgraaddatastel bestaan uit die getalle 10, 8, 10, 8, 8 en 4.

2. Versamel al jou data. Jy benodig elke getal in jou steekproef om die gemiddelde te bereken.

3. Voeg die getalle in jou steekproef bymekaar. Dit is die eerste stap in die berekening van die rekenkundige gemiddelde, of gemiddelde.

4. Deel die som deur die aantal getalle in jou steekproef (n). Bereken die gemiddelde van alle data.
Metode 2 van 3: Vind die variansie in jou steekproef

1. Bepaal die variansie. Die variansie is `n getal wat die verspreiding van jou waardes rondom die gemiddelde aandui.
- Hierdie nommer sal jou `n idee gee van hoeveel die waardes van mekaar verskil.
- Lae variansiemonsters bevat waardes wat min van die gemiddelde verskil.
- Hoë variansie monsters bevat waardes wat baie van die gemiddelde afwyk.
- Die variansie word dikwels gebruik om die verspreiding van waardes in twee datastelle te vergelyk.

2. Trek die gemiddelde van elk van die getalle in jou steekproef af. Jy kry nou `n reeks waardes wat aandui hoeveel elke getal in die steekproef van die gemiddelde verskil.

3. Kwadra al die getalle wat jy in die vorige stap bereken het. Jy het al hierdie waardes nodig om die variansie van jou steekproef te bepaal.

4. Tel die kwadraatgetalle bymekaar. Dit is die som van die vierkante.

5. Deel die som van vierkante deur (n-1). Onthou dat n die aantal getalle in die steekproef voorstel. Deur hierdie stap uit te voer, bepaal jy die variansie.
Metode 3 van 3: Berekening van die standaardafwyking

1. Let op die afwyking. Jy het hierdie waarde nodig om die standaardafwyking van jou steekproef te bereken.
- Onthou dat die afwyking is hoeveel die waardes van die gemiddelde afwyk.
- Die standaardafwyking is `n soortgelyke waarde wat die verspreiding van die getalle in jou steekproef aandui.
- In ons voorbeeld van toetsgrade was die afwyking 4,8.

2. Bereken die vierkantswortel van die variansie. Die resultaat hiervan is die standaardafwyking.

3. Bereken weer die gemiddelde, variansie en standaardafwyking. Hoe om jou antwoord na te gaan.
Artikels oor die onderwerp "Bereken standaardafwyking"
Оцените, пожалуйста статью
Gewilde