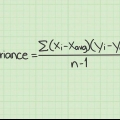Berekening van variansie: 8 stappe (met prente)

Inhoud

Trappe
Wenke

Deur die variansie te bereken, kan u die verspreiding van `n stel waardes meet - die mate waarin `n aantal waardes van mekaar verskil. Variansie is een van die komponente van die waarskynlikheidsverdeling en dui aan in watter mate waardes van die gemiddelde afwyk. Variansie word dikwels saam met die standaardafwyking (die vierkantswortel van die variansie) gebruik. As jy wil weet hoe om die variansie van `n stel waardes te bereken, volg die stappe hieronder.

Trappe

1. Skryf die formule vir die berekening van die variansie. Die skatting vir die berekening van `n ewekansige skatting van die populasievariansie uit `n vaste steekproef van n waarnemings is die volgende definisie:(s) = Σ [(x_i - x̅)]/n - 1. Die formule vir die berekening van die variansie in `n hele populasie is dieselfde as die vorige een, behalwe dat die noemer nie gelyk is aan n – 1 nie, maar aan n. Solank jy met `n eindige stel waarnemings te doen het, is dit beter om die eerste formule te gebruik. Hier is `n verduideliking van die formule se veranderlikes:

s = Variansie
Σ = Opsomming, die som van alle terme in die vergelyking na die somteken.
X_i = Die steekproefwaardes.
x̅ = Die gemiddelde van die waardes in die reeks.
n = Die steekproefgrootte. Die aantal waardes in die reeks.

2. Bereken die som van die waardes in die reeks. Skep eers `n tabel met `n kolom vir die waardes, die waarde minus die gemiddelde (x_i - x̅) en dan die kwadraat van hierdie terme [(x_i - X))]. Nadat jy klaar is met die tabel en die eerste kolom gevul is, tel al die waardes in die reeks by. Gestel jy het te doen met die volgende reeks getalle: 17, 15, 23, 7, 9, 13. Bygetel is dit: 17 + 15 + 23 + 7 + 9 + 13 = 84.

3. Bereken die gemiddelde. Deel die som van die getalle in die reeks deur die aantal elemente in die reeks om die gemiddelde te bereken. So in hierdie geval die som 84 gedeel deur die aantal getalle, 6. 84/6 = 14. skryf "14" heel onder in die kolom as `n gemiddelde.

4. Trek die gemiddelde van elke waarde van die reeks af. Trek 14 van elke waarde in die reeks af en vul die derde kolom in (die steekproefgemiddeld). Jy kan jou werk nagaan deur te kyk of die som van alle resultate nul is. Hier is hoe om die afwyking van die gemiddelde vir elke waarde in die reeks te bereken:

17 - 14 = 3

15 - 14 = 1

23 - 14 = 9

7 - 14 = -7

9 - 14 = -5

13 - 14 = -1

5. Vierkant elke resultaat. Nadat jy die afwyking van die gemiddelde bereken het, vierkantig dit en skryf die antwoord in die vierde kolom neer. Alle antwoorde is dus positief. Hier is hoe dit uitgewerk het:

3 = 9

1 = 1

9 = 81

(-7)= 49

(-5) = 25

(-1)= 1

6. Bereken die som van vierkante. Voeg die resultate bymekaar. 9 + 1 + 81 + 49 + 25 + 1 = 166

7. Vervang die waardes in die vergelyking. Vul die waardes in die vergelyking in. Onthou dat "n" verteenwoordig die aantal elemente in die ry.

s = 166/(6-1)

8. Los op. Deel nou 166 deur 5. Die resultaat is 33,2. As jy ook die standaardafwyking wil weet, vind die vierkantswortel van 33.2. √33.2 = 5.76. Nou kan jy begin om hierdie data in verhouding tot die groot prentjie te interpreteer. Gewoonlik word die variansie van twee reekse vergelyk. Die laagste waarde beteken dat in daardie reeks die variansie minder groot is.