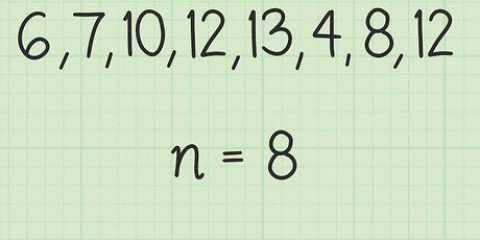In ons voorbeeld was 310 die huidige waarde en 205 was die vorige waarde. Die formule lyk dus so met hierdie waardes: (310 - 205)/205 = 105/205 = 0,51 
So in ons voorbeeld vermenigvuldig ons 0,51 met 100 en dan tel ons `n persentasieteken by. 0,51 x 100 = 51%. Ons groeifaktor is dus 51%. Met ander woorde, die huidige waarde is 51% groter as die vorige waarde. As die huidige waarde minder as die vorige waarde was, sou die groeifaktor negatief gewees het. 

Deur hierdie metode te gebruik, bereken ons die gemiddelde groeifaktor vir elke tydinterval, met die veronderstelling dat groei proporsioneel toeneem. Aangesien ons jare in ons voorbeeld gebruik, kry ons `n gemiddelde jaarliks groei faktor. 
Jy behoort nou te kry: groeifaktor = (huidige/vorige) - 1 . 
In ons voorbeeld gebruik ons as huidige waarde 310 en as vorige waarde 205, vir die tydperk wat ons 10 jaar neem vir n. In hierdie geval, die gemiddelde jaarlikse groeifaktor (310/205) - 1 = 0,0422 0,0422 x 100 = 4,22%. Die waarde het gemiddeld met 4,22 persent per jaar toegeneem.
Bereken 'n groeifaktor
Inhoud
Vir baie lesers, "`n groeifaktor te bereken" soos `n intimiderende wiskundige proses. In werklikheid is die berekening van die groeifaktor baie eenvoudig. `n Groeifaktor is bloot die verskil tussen twee waardes, uitgedruk as `n persentasie van die eerste waarde. In hierdie artikel sal ons die basiese metode verduidelik en jou `n paar meer ingewikkelde maniere wys om groei te meet.
Trappe
Deel 1 van 2: Berekening van `n groeifaktor

1. Kry data wat `n verandering oor tyd toon. Al wat jy nodig het om `n groeifaktor te bereken is twee getalle - `n getal wat die beginwaarde aandui en `n getal wat die eindwaarde aandui. Gestel jou maatskappy was $1 000 werd aan die begin van die maand en dit is nou $1 200 werd aan die einde van die maand. Dan kan jy die groeifaktor met 1000 as die beginwaarde (die vorige waarde) en 1200 as die finale waarde (die huidige waarde) bereken. Kom ons los `n eenvoudige voorbeeldsom op. In hierdie geval gebruik ons die getalle 205 (vorige waarde) en 310 (huidige waarde).
- As die getalle dieselfde is, is daar geen groei nie - die groeifaktor is dan 0.

2. Pas die formule toe vir die berekening van die groeifaktor. Voer die waardes in die volgende formule in: (huidig) - (vorige) / (vorige). Die antwoord sal `n breuk wees. Skakel die breuk om na `n desimale waarde.

3. Skakel die oplossing om na persentasies. Gewoonlik word `n groeifaktor as `n persentasie getoon. Om die desimale oplossing om te skakel, vermenigvuldig ons die getal met honderd en voeg die persentasieteken by. `n Persentasie is `n maklik verstaanbare manier om die verandering tussen twee waardes aan te dui.
Deel 2 van 2: Berekening van die gemiddelde groeifaktor oor gereelde tydintervalle

1. Organiseer jou data in `n tabel. Dit is nie nodig nie, maar kan nuttig wees, want dit laat jou toe om die data as `n reeks waardes oor `n tydperk te sien. Vir hierdie doel kan jy `n eenvoudige tabel skep - skep twee kolomme, plaas die waardes van tyd in die linkerkolom en die waardes van hoeveelheid in die regterkolom.

2. Gebruik `n groeifaktorvergelyking wat die aantal tydintervalle in jou data in ag neem. Jou data moet gereelde intervalle bevat, en elke waarde moet `n ooreenstemmende hoeveelheid waarde hê. Die tydeenhede is nie belangrik nie - die metode werk vir data wat in `n bestek van sekondes, minute, dae ensovoorts ingesamel word. In ons geval is die data in jare. Voer jou vorige en huidige waardes in `n nuwe formule in: (huidig) = (vorige) * (1+ groeifaktor), waar n vir aantal tydperke staan.

3. Isoleer die groeifaktorveranderlike. Wysig die vergelyking totdat slegs die groeitempo aan die een kant van die vergelyking is. Om dit te doen, deel ons beide kante deur die vorige waarde, neem die eksponent van 1/n, en trek dan 1 af.

4. Los op om die groeifaktor te bereken. Voer die waardes vir vorige en huidige in, en vervang n met die aantal tydintervalle van jou data, insluitend vorige en huidige waardes. Los op volgens die basiese wiskundige beginsels.
Wenke
- Dit werk beide maniere. Gebruik dieselfde formule as die getalle op of af gaan. Ons praat van `n verlangsaming in groei as die getalle daal.
- Die volledige formule vir die berekening van `n groeikoers is soos volg: (huidige - vorige) / vorige) * 100
Artikels oor die onderwerp "Bereken 'n groeifaktor"
Оцените, пожалуйста статью
Soortgelyk
Gewilde