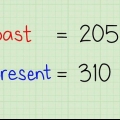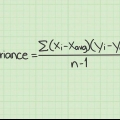Hoe om Spearman se rangkorrelasiekoëffisiënt te bereken

Inhoud

Trappe
Wenke
Waarskuwings

Met Spearman se rangkorrelasiekoëffisiënt kan jy sien of twee veranderlikes verwant is deur `n monotoniese funksie (d.w.Z. dat as een getal toeneem, die ander getal ook toeneem of andersom). Om Spearman se rangkorrelasiekoëffisiënt te bereken, moet jy datastelle orden en vergelyk om Σd te vind, en dan daardie waarde in die standaard of vereenvoudigde weergawe van Spearman se rangkorrelasiekoëffisiëntformule invoer. Jy kan ook hierdie koëffisiënt met Excel-formules of R-opdragte bereken.

Trappe

Metode 1 van 3: Handmatig

1. Teken jou datatabel. Organiseer die inligting wat jy nodig het om Spearman se rangkorrelasiekoëffisiënt te bereken. Jy benodig:

6 kolomme met opskrifte, soos hierbo getoon.
Soveel rye as wat jy datapare het.

2. Vul die eerste twee kolomme met jou datapare.

3. Rangskik die datapunte van die eerste kolom in die derde kolom, van 1 tot n (die totale aantal datapunte wat jy het). Gee die laagste getal posisie 1, die volgende getal posisie 2, ensovoorts.

4. Doen dieselfde met die vierde kolom soos in stap 3, maar rangskik nou die tweede kolom.

As jy twee (of meer) datapunte met dieselfde waarde in `n kolom het, neem die gemiddelde van die posisies wat daardie datapunte normaalweg sou hê, en gee die datapunte hierdie gemiddelde as hul nuwe posisie.
In die voorbeeld aan die regterkant is daar twee vyfs wat normaalweg in posisie 2 en 3 sal wees. Dit is twee dieselfde liedjies, so neem die gemiddelde van hul posisies. Die gemiddeld van 2 en 3 is 2,5, dus gee albei vye posisie 2,5.

5. In die kolom `d`, bereken die verskil tussen die twee posisies in elke datapaar. Met ander woorde, as een posisie 1 het en die ander het posisie 3, is die verskil 2. (Positief of negatief maak nie saak nie, aangesien ons hierdie verskil in die volgende stap gaan vier.)

6. Kwadreer die waardes in die d-kolom en skryf hierdie waardes in die d-kolom.

7. Voeg alle datapunte in die d-kolom bymekaar. Hierdie waarde is Σd.

8. Kies een van die formules hieronder:

Indien geen gelyke datapunte in die vorige stappe voorgekom het nie, voer Σd in die eenvoudige formule vir Spearman se rangkorrelasiekoëffisiënt in

en voer die aantal datapare vir `n` in om jou antwoord te vind.

As soortgelyke datapunte wel in die vorige stappe voorgekom het, gebruik die standaardformule vir Spearman se rangkorrelasiekoëffisiënt:

9. Interpreteer die resultaat. Dit kan wissel tussen -1 en 1.

Naby aan -1 – Negatiewe korrelasie.

Naby 0 – Geen lineêre korrelasie nie.

Naby 1 – Positiewe korrelasie.

Metode 2 van 3: In Excel

1. Skep nuwe kolomme met die posisies van die bestaande kolomme. Byvoorbeeld, as jy jou data in Kolom A2:A11 het, sal jy die formule `=RANK(A2,A$2:A$11)` gebruik en die reeks oor al jou rye en kolomme uitbrei.

2. Behandel gelyke datapunte soos beskryf in stappe 3 en 4 van metode 1.

3. In `n nuwe sel, maak `n korrelasieberekening tussen die twee kolomme met `n formule soos `=CORREL(C2:C11,D2:D11)`. In hierdie geval is C en D die posisiekolomme. Spearman se rangkorrelasiekoëffisiënt verskyn in die korrelasiesel.

Metode 3 van 3: Met R

1. Installeer R as jy dit nie reeds het nie. (Sien https://www.r-projek.org/.)

2. Stoor jou data as `n CSV-lêer, met die data wat jy wil korreleer in die eerste twee kolomme. Jy kan dit doen met die `Stoor as`-kieslys.

3. Maak die R-redigeerder oop. As jy in die terminale werk, hardloop eenvoudig R. Wanneer jy op jou lessenaar is, klik die R-logo.

4. Tik die volgende opdragte:

d <- lees.csv("NAME_OF_YOU_CSV.csv") en druk enter

cor(rang(d[,1]),rang(d[,2]))

Wenke

Vir die meeste datastelle het jy ten minste vyf pare data nodig om `n neiging vas te stel (slegs drie pare is in die voorbeeld gebruik om die voorbeeld makliker te maak).

Waarskuwings

Spearman se rangkorrelasiekoëffisiënt toon slegs korrelasiesterkte as die datapunte voortdurend toeneem of afneem. As die verspreidingsdiagram van die datapunte `n ander neiging toon, sal Spearman se rangkorrelasiekoëffisiënt die korrelasie verhoog nie korrek vertoon.
Hierdie formule is gebaseer op die aanname dat daar nie gelyke datapunte is nie. As daar gelyke datapunte is, soos in die voorbeeld hierbo, gebruik die volgende definisie: die produk-oomblikkorrelasiekoëffisiënt vir die geledere.