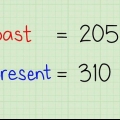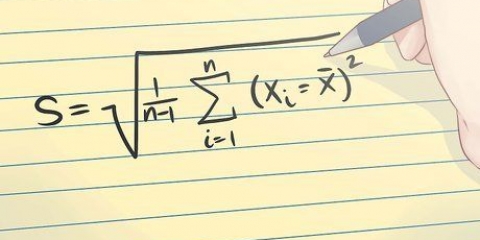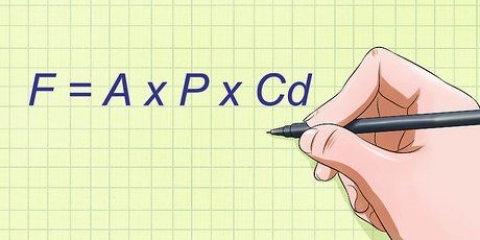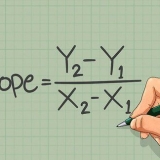Berekening van kovariansie

Inhoud

Trappe
Waarskuwings

Kovariansie is `n statistiese berekening om die verhouding tussen twee stelle data meer deursigtig te maak. Gestel byvoorbeeld dat antropoloë die lengte en gewig van `n bevolking binne `n bepaalde kultuur bestudeer. Vir elke persoon in die studie kan lengte en gewig voorgestel word met `n datapaar (x, y). Hierdie waardes kan in `n standaardformule gebruik word vir die berekening van die kovariansieverhouding. Hierdie artikel verduidelik eers die berekeninge vir die bepaling van die kovariansie van `n datastel. Vervolgens sal twee ander outomatiese maniere om die resultaat te bepaal bespreek word.

Trappe

Metode 1 van 4: Bereken die kovariansie met die hand deur die standaardformule te gebruik

Prent getiteld Bereken kovariansie Stap 1

1. Leer die standaard kovariansieformule en sy dele. Die standaardformule vir die berekening van die kovariansie is

Σ (X i - X_{gem}) (y_{i} - y_{gem}) / (n - 1)

$Sigma (x_{i}-x_{{text{gem}}})(y_{i}-y_{{text{gem}}})/(n-1)$ . Om hierdie formule te gebruik, moet jy die betekenis van die veranderlikes en simbole ken:

$Σ$ $Sigma$ - Hierdie simbool is die Griekse letter `sigma`. In wiskundige funksies beteken dit om `n reeks by te voeg van wat volg. In hierdie formule beteken die Σ-teken dat jy die waardes in die teller van die breuk bereken, dan almal bymekaar tel en dan die totaal deur die noemer deel.
$X i$ $XI}$ - Jy kan hierdie veranderlike lees as `x sub i`. Die subskripsie i verteenwoordig `n teller. Dit beteken jy gaan `n berekening doen vir elke waarde van x in jou datastel.
$X a v g$ $x_{{gem}}$ - Die `avg` dui aan dat x(avg) die gemiddelde waarde van alle x datapunte is. Die gemiddelde word soms geskryf as `n x met `n kort horisontale lyn daarbo. In daardie styl lees jy die veranderlike as `x-bar`, maar dit beteken steeds die gemiddelde van die datastel.
$y i$ $y_{i}$ - Jy kan hierdie veranderlike lees as `y sub i`. Die subskripsie i is die teller. Dit beteken jy gaan `n berekening doen vir elke waarde van y in jou datastel.
$y a v g$ $y_{{gem}}$ - Die `avg` dui aan dat y(avg) die gemiddelde waarde van al x datapunte is. Die gemiddelde word soms geskryf as `n y met `n kort horisontale lyn daarbo. In daardie styl lees jy die veranderlike as `y-bar`, maar dit beteken steeds die gemiddelde van die datastel.
$n$ $n$ - Hierdie veranderlike is die aantal elemente in jou datastel. Onthou dat in `n kovariansieprobleem `n enkele `element` saamgestel is uit beide `n x-waarde en `n y-waarde. Die waarde `n` is die aantal pare datapunte, nie individuele getalle nie.

Prent getiteld Bereken kovariansie Stap 2

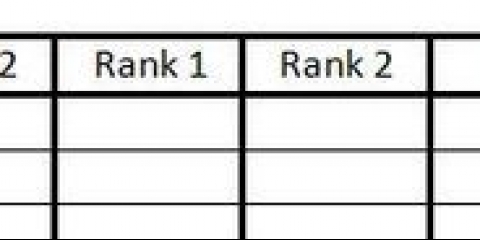
2. Konstrueer jou datatabel. Voordat u begin, is dit nuttig om u data in te samel. Skep `n tabel met vyf kolomme. Jy moet elke kolom soos volg verklaar:

X

$X$ - Vul hierdie kolom met die waardes van die punte van die x-data.

y

$y$ - Vul hierdie kolom met die waardes van die y-data. Maak seker dat die y-waardes in lyn is met die ooreenstemmende x-waardes. In `n kovariansieprobleem is die volgorde van die datapunte en die koppeling van x en y belangrik.

(X i - X_{gem})

$(x_{i}-x_{{text{gem}}})$ - Laat hierdie kolom aan die begin leeg. Jy gaan dit met data vul nadat jy die x-data gemiddeld het.

(y i - y_{gem})

$(y_{i}-y_{{text{gem}}})$ - Laat hierdie kolom aan die begin leeg. Jy gaan dit met data vul nadat jy die y-data gemiddeld het.

Produk

${text{Produk}}$ - Laat die laaste kolom ook leeg. Dit sal tydens die verwerking van die opdrag ingevul word.

Prent getiteld Bereken kovariansie Stap 3

3. Bereken die gemiddelde van die x datapunte. Hierdie voorbeelddataversameling bevat 9 nommers. Om die gemiddelde te vind, tel hulle bymekaar en deel die som deur 9. Dit gee die resultaat 1 + 3 + 2 + 5 + 8 + 7 + 12 + 2 + 4 = 44. As jy dit deur 9 deel, kry jy die gemiddelde 4,89. Dit is die waarde wat jy as x(gem) sal gebruik vir die komende berekeninge.

Prent getiteld Bereken kovariansie Stap 4

4. Bereken die gemiddelde van die y datapunte. Hierdie y-kolom moet ook uit 9 datapunte bestaan wat met die x datapunte saamval. Bepaal die gemiddelde hiervan. Vir hierdie voorbeelddatastel word dit 8 + 6 + 9 + 4 + 3 + 3 + 2 + 7 + 7 = 49. Deel hierdie totaal deur 9 om `n gemiddeld van 5,44 te kry. Jy gaan 5.44 gebruik as die waarde van y(gemiddeld) vir die komende berekeninge.

Prent getiteld Bereken kovariansie Stap 5

5. Bereken die waardes (Xi-Xgem){displaystyle (x_{i}-x_{text{gem}})} $(x_{i}-x_{{text{gem}}})$ . Vir elke element in die x-kolom, bereken die verskil tussen daardie getal en die gemiddelde waarde. Vir hierdie voorbeeldprobleem beteken dit om 4,89 van elke x-waarde af te trek. As die oorspronklike datapunt minder as die gemiddelde is, sal jou resultaat negatief wees. As die oorspronklike datapunt groter is as die gemiddelde, sal die resultaat positief wees. Maak seker dat jy tred hou met watter waardes negatief is.

Byvoorbeeld, die eerste datapunt in die x-kolom is 1. Die waarde om op die eerste reël van die kolom in te voer

(X i - X_{gem})

$(x_{i}-x_{{text{gem}}})$ is: 1 – 4.89 = -3.89.

Herhaal hierdie proses vir elke datapunt. Die tweede reël word dus: 3 - 4.89 = -1.89. Die derde reël word: 2 - 4.89 = -2.89. Gaan voort met hierdie proses vir alle datapunte. Die nege getalle in hierdie kolom word: -3.89, -1.89, -2.89, 0.11, 3.11, 2.11, 7.11, -2.89, -0.89.

Prent getiteld Bereken kovariansie Stap 6

6. Bereken die waardes (yi-ygem){displaystyle (y_{i}-y_{text{gem}})} $(y_{i}-y_{{text{gem}}})$ . In hierdie kolom gaan jy soortgelyke aftrekkings doen deur die y-datapunte en die y-gemiddelde te gebruik. As die oorspronklike datapunt minder as die gemiddelde is, sal die resultaat negatief wees. As die oorspronklike datapunt groter is as die gemiddelde, sal jou resultaat positief wees. Maak seker dat jy tred hou met watter waardes negatief is.

So vir die eerste reël sal jou berekening wees: 8 -5.44, = 2.56.

Die tweede reël word: 6 – 5.44 = 0.56.

Hou aan om die waardes af te trek tot aan die einde van die datalys. Wanneer jy klaar is, behoort jy die volgende nege waardes in hierdie kolom te hê: 2.56, 0.56, 3.56, -1.44, -2.44, -2.44, -3.44 , 1.56, 1.56.

Prent getiteld Bereken kovariansie Stap 7

7. Bereken die produkte vir elke datary. Jy vul die rye van die laaste kolom in deur die getalle wat jy in die twee vorige kolomme bereken het te vermenigvuldig

(X i - X_{gem})

$(x_{i}-x_{{text{gem}}})$ en

(y i - y_{gem})

$(y_{i}-y_{{text{gem}}})$ . Werk jou pad ry vir ry, vermenigvuldig die twee getalle met hul ooreenstemmende datapunte. Wees op die uitkyk vir enige negatiewe waardes langs die pad.

In die eerste ry van hierdie voorbeelddata, die

(X i - X_{gem})

$(x_{i}-x_{{text{gem}}})$ jy het -3.89 bereken, en die

(y i - y_{gem})

$(y_{i}-y_{{text{gem}}})$ waarde 2,56. Die produk van hierdie twee getalle is: -3.89 x 2.56 = -9.96.

Vir die tweede ry, vermenigvuldig die twee getalle: -1,88 x 0,56 = -1,06.

Hou aan om ry vir ry te vermenigvuldig tot aan die einde van die datastel. Wanneer jy klaar is, moet die nege waardes in hierdie kolom lees: -9.96, -1.06, -10.29, -0.16, -7.59, -5.15, -24.46 , -4.51, -1.39.

Prent getiteld Bereken kovariansie Stap 8

8. Vind die som van die waardes in die laaste kolom. Dit is waar die Σ-simbool inkom. Nadat jy al die berekeninge tot dusver gedoen het, tel die resultate bymekaar. Vir hierdie voorbeelddatastel behoort jy nou nege waardes in die laaste kolom te hê. Tel daardie nege getalle bymekaar. Let goed op of `n getal positief of negatief is.

Die som van hierdie steekproefdatastel behoort op te tel tot -64.57. Skryf hierdie totaal in die spasie onderaan die kolom. Dit is die waarde van die teller van die standaard kovariansieformule.

Prent getiteld Bereken kovariansie Stap 9

9. Bereken die noemer van die kovariansieformule. Die teller van die standaard kovariansieformule is die waarde wat jy pas bereken het. Die noemer word voorgestel deur (n-1), en is een minder as die aantal pare van die data in jou datastel.

In hierdie voorbeeldprobleem is daar nege pare data, dus n is 9. Daarom is die waarde van (n-1) gelyk aan 8.

Prent getiteld Bereken kovariansie Stap 10

10. Verdeel die teller deur die noemer. Die laaste stap in die berekening van die kovariansie is om die teller te deel,

Σ (X i - X_{gem}) (y_{i} - y_{gem})

$Sigma (x_{i}-x_{{text{gem}}})(y_{i}-y_{{text{gem}}})$ deur die noemer,

(n - 1)

$(n-1)$ . Die kwosiënt is die kovariansie van jou data.

Vir hierdie voorbeelddatastel is hierdie berekening: -64.57/8 = -8.07.

Metode 2 van 4: Bereken kovariansie deur `n Excel-werkblad te gebruik

Prent getiteld Bereken kovariansie Stap 11

1. Let op wat die herhalende berekeninge is. Kovariansie is `n berekening wat jy `n paar keer met die hand moet doen sodat jy die betekenis van die resultaat verstaan. As jy egter gereeld kovariansie gaan gebruik om data te interpreteer, het jy `n vinniger en outomatiese manier nodig om die resultate te kry. Jy het dalk nou al opgemerk dat met ons relatief klein datastel van net nege pare data, die berekeninge bestaan het uit twee gemiddeldes, agtien afsonderlike aftrekkings, nege vermenigvuldiging, een optelling en uiteindelik nog `n deling. Dit is 31 relatief klein berekeninge om die oplossing te vind. Langs die pad loop jy die risiko om negatiewe tekens te mis of die resultate verkeerd te kopieer, wat veroorsaak dat die antwoord verkeerd is.

Prent getiteld Bereken kovariansie Stap 12

2. Skep `n werkblad vir die berekening van die kovariansie. As jy vertroud is met Excel (of enige ander berekeningsprogram), kan jy maklik `n tabel skep om die kovariansie te bepaal. Benoem die opskrifte van die vyf kolomme net soos in die handberekeninge: x, y, (x(i)-x(gemiddeld)), (y(i)-y(gemiddeld)) en Produk.

Om die benaming te vereenvoudig, noem die derde kolom iets soos "x verskil" en die vierde kolom "y verskil," solank jy die betekenis van die data onthou.

As die tabel in die boonste linkerhoek van die werkblad begin, sal sel A1 gemerk word as x, terwyl die ander byskrifte sal voortgaan na sel E1.

Prent getiteld Bereken kovariansie Stap 13

3. Vul die datapunte in. Tik die datawaardes in die twee kolomme x en y. Onthou dat die volgorde van die datapunte saak maak, dus moet jy elke y met die ooreenstemmende waarde van x pas.

Die x-waardes begin in sel A2 en gaan voort tot by die aantal datapunte wat jy benodig.

Die y-waardes begin in sel B2 en gaan voort tot by die aantal datapunte wat jy benodig.

Prent getiteld Bereken kovariansie Stap 14

4. Bepaal die gemiddelde van die x- en y-waardes. Excel bereken die gemiddeldes baie vinnig vir jou. Tik in die eerste leë sel onder elke kolom data die formule =AVERAGE(A2:A___). Vul die spasie met die nommer van die sel wat ooreenstem met jou laaste datapunt.

Byvoorbeeld, as jy 100 datapunte het, sal selle A2 tot A101 gevul word, so in die sel sal jy tik: = AVERAGE(A2:A101).

Vir die y-data, tik die formule = AVERAGE(B2:B101).

Onthou dat `n formule in Excel met `n `=`-teken begin.

Prent getiteld Bereken kovariansie Stap 15

5. Tik die formule vir die kolom (x(i)-x(gem)). In sel C2, voer die formule in vir die berekening van die eerste aftrekking. Hierdie formule word: =A2-___. Vul die leë spasie met die seladres wat die gemiddelde van die x-data bevat.

Byvoorbeeld, die 100 datapunte word gemiddeld in sel A103, so jou formule word: =A2-A103.

Prent getiteld Bereken kovariansie Stap 16

6. Herhaal die formule vir die datapunte (y(i)-y(gemiddeld)). Na dieselfde voorbeeld sal dit in sel D2 wees. Die formule word: =B2-B103.

Prent getiteld Bereken kovariansie Stap 17

7. Tik die formule vir die `Produk`-kolom. In die vyfde kolom moet jy in sel E2 die formule tik vir die berekening van die produk van die twee voorafgaande selle. Dit word dan: =C2*D2.

Prent getiteld Bereken kovariansie Stap 18

8. Kopieer die formules om die tabel te vul. Tot dusver het jy net die eerste paar datapunte in ry 2 geprogrammeer. Merk selle C2, D2 en E2 met jou muis. Plaas jou wyser op die klein blokkie in die onderste regterhoek totdat `n plusteken verskyn. Klik en hou die muisknoppie en sleep die muis af om die keuse uit te brei en die hele datatabel te vul. Hierdie stap sal outomaties die drie formules van selle C2, D2 en E2 na die hele tabel kopieer. Die tabel moet outomaties gevul word met al die berekeninge.

Prent getiteld Bereken kovariansie Stap 19

9. Programmeer die som van die laaste kolom. Jy benodig die som van die items in die `Produk`-kolom. Tik die formule in die leë sel direk onder die laaste datapunt in daardie kolom: =SUM(E2:E___). Vul die spasie met die seladres van die laaste datapunt.

In die voorbeeld met 100 datapunte gaan hierdie formule in sel E103. Tipe: =SOM(E2:E102).

Prent getiteld Bereken kovariansie Stap 20

10. Bepaal die kovariansie. Jy kan ook vir Excel die finale berekening vir jou laat doen. Die laaste berekening in sel E103 in ons voorbeeld verteenwoordig die teller van die kovariansieformule. Tik onmiddellik onder daardie sel die formule: =E103/___. Vul die spasie met die aantal datapunte wat jy het. In ons voorbeeld is dit 100. Die resultaat is die kovariansie van jou data.

Metode 3 van 4: Gebruik aanlyn kovariansie sakrekenaars

Prent getiteld Bereken kovariansie Stap 21

1. Soek aanlyn vir kovariansie sakrekenaars. Verskeie skole, maatskappye of ander bronne het webwerwe wat die kovariansiewaardes baie maklik vir jou bereken. Gebruik die soekterm `kovariansie sakrekenaar` in `n soekenjin.

Prent getiteld Bereken kovariansie Stap 22

2. Voer jou besonderhede in. Lees asseblief die instruksies op die webwerf noukeurig deur om seker te maak dat u die inligting korrek invoer. Dit is belangrik dat u datapare in orde gehou word, anders sal die gegenereerde resultaat `n verkeerde kovariansie wees. Webwerwe het verskillende data-invoerstyle.

Op die webwerf http://nrekenaars.com/statistieke/kovariansie-sakrekenaar.htm, is daar byvoorbeeld `n horisontale blokkie om die x-waardes in te voer en `n tweede horisontale blokkie om die y-waardes in te voer. Jy moet jou data geskei deur kommas invoer. Dus, die x-datastel wat vroeër in hierdie artikel bereken is, moet dan ingevoer word as 1,3,2,5,8,7,12,2,4. Die y-data as 8,6,9,4,3,3,2,7,7.

Op `n ander webwerf, https://www.die sakrekenaar.co/math/Covariance-Calculator-705.html, jy sal gevra word om die x-data in die eerste blokkie in te voer. Data word vertikaal ingevoer, met een item per reël. Daarom lyk die inskrywing op hierdie webwerf soos volg:

Prent getiteld Bereken kovariansie Stap 23

3. Bereken jou resultate. Die aantreklike ding van hierdie aanlyn berekeninge is dat jy na die invoer van die data gewoonlik net op die `Bereken`-knoppie hoef te klik, waarna die resultate outomaties verskyn. Die meeste werwe sal jou voorsien van die intermediêre berekeninge van x(gemiddeld), y(gemiddeld) en n.

Metode 4 van 4: Interpreteer die resultate van die kovariansie

Prent getiteld Bereken kovariansie Stap 24

1. Soek `n positiewe of negatiewe verhouding. Die kovariansie is `n enkele statistiese getal wat die verband tussen een datastel en `n ander aandui. In die voorbeeld wat in die inleiding genoem word, word die lengte en gewig gemeet. Jy sou verwag dat namate mense groei, hul gewig ook sal toeneem, wat lei tot `n positiewe kovariansie siening. Nog `n voorbeeld: Veronderstel dat data ingesamel word wat die aantal ure aandui wat `n persoon al gholf geoefen het en die telling wat hy of sy behaal. In hierdie geval verwag jy `n negatiewe kovariansie, wat beteken dat namate die aantal oefenure toeneem, die gholftelling sal afneem. (In gholf is `n laer telling beter).

Beskou die steekproefdatastel wat hierbo bereken is. Die gevolglike kovariansie is -8.07. Die minus teken beteken dat as die x-waardes toeneem, die y-waardes geneig is om af te neem. Jy kan sien dat dit waar is deur na sommige van die waardes te kyk. Byvoorbeeld, die x-waardes van 1 en 2 stem ooreen met die y-waardes van 7, 8 en 9. Die x-waardes van 8 en 12 is gekoppel aan die y-waardes van onderskeidelik 3 en 2 .

Prent getiteld Bereken kovariansie Stap 25

2. Interpreteer die grootte van die kovariansie. As die getal van die kovariansietelling groot is, hetsy `n groot positiewe getal of `n groot negatiewe getal, dan kan jy dit interpreteer as twee data-elemente wat sterk verbind is, hetsy op `n positiewe of negatiewe manier.

Die kovariansie -8.07 van die steekproefdatastel is redelik groot. Let daarop dat die data wissel van 1 tot 12. So 8 is nogal `n groot getal. Dit dui op `n redelik sterk verband tussen die datastelle x en y.

Prent getiteld Bereken kovariansie Stap 26

3. Verstaan die gebrek aan `n verhouding. As jou resultaat `n kovariansie gelyk aan of baie naby aan 0 is, kan jy aflei dat die datapunte geen verband het nie. Dit wil sê, `n toename in een waarde mag, maar hoef nie tot `n toename in die ander te lei nie. Die twee terme word byna arbitrêr verbind.

Gestel jy bring skoengroottes in verband met eksamengrade. Omdat daar soveel faktore is wat `n student se eksamenpunte beïnvloed, is `n kovariansietelling naby 0 te verwagte. Dit dui daarop dat daar byna geen verband tussen die twee waardes is nie.

Prent getiteld Bereken kovariansie Stap 27

4. Bekyk die verhouding grafies. Om kovariansie visueel te verstaan, kan jy jou datapunte in `n x,y grafiek plot. Wanneer jy dit doen, behoort jy redelik maklik te sien dat die punte, hoewel nie presies in `n reguit lyn nie, geneig is om `n groep in `n diagonale lyn van links bo na regs onder te nader. Dit is die beskrywing van `n negatiewe kovariansie. Jy sien ook dat die waarde van die kovariansie -8.07 is. Dit is nogal `n groot getal in vergelyking met die datapunte. Die hoë getal dui daarop dat die kovariansie redelik sterk is, wat afgelei kan word uit die lineêre vorm van die datapunte.

Om dit weer te hersien, lees wikiHow-artikels oor tekenpunte in `n koördinaatstelsel.

Waarskuwings

Kovariansie het beperkte toepassing in statistieke. Dit is dikwels `n stap in die rigting van die berekening van korrelasiekoëffisiënte of ander konsepte. Wees versigtig vir té vet interpretasies gebaseer op `n kovariansietelling.