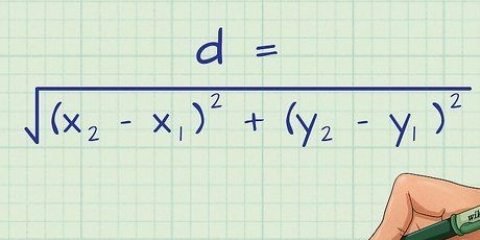Gebruik die Pythagoras-stelling: 12 stappe (met prente)

Inhoud

Trappe
- Metode 1 van 2: Die lengte van die sye van `n reghoekige driehoek
- Metode 2 van 2: Bereken die afstand tussen twee punte in die vlak
Wenke

Die Pythagoras-stelling beskryf die lengte van die sye van `n reghoekige driehoek op `n manier so elegant en prakties dat dit vandag nog algemeen gebruik word. Dit stel dat vir enige reghoekige driehoek, die som van die vierkante van die regte sye gelyk is aan die kwadraat van die skuinssy. Met ander woorde, vir `n reghoekige driehoek (`n driehoek met sye wat loodreg op mekaar is), met sye van lengte a en b en `n skuinssy van lengte c: a + b = c. Die Pythagoras-stelling is een van die pilare van meetkunde en het talle praktiese toepassings – byvoorbeeld, deur hierdie stelling te gebruik is dit baie maklik om die afstand tussen twee punte in `n vlak te vind.

Trappe

Metode 1 van 2: Die lengte van die sye van `n reghoekige driehoek

Prent getiteld Gebruik die Pythagoras-stelling Stap 1

1. Kyk of jy met `n reghoekige driehoek te doen het. Die Pythagoras-stelling kan slegs vir reghoekige driehoeke gebruik word, dus voordat jy voortgaan is dit belangrik om vas te stel dat jou driehoek aan die definisie van `n reghoekige driehoek voldoen. Gelukkig is hier net een deurslaggewende faktor - een van die hoeke van die driehoek moet `n 90 grade hoek wees.

Een leidraad is dat regte hoeke dikwels met `n klein vierkantige hakie gemerk word om aan te dui dat dit `n 90 grade hoek is. Kyk of daar so `n hakie in een van die hoeke van jou driehoek is.

Prent getiteld Gebruik die Pythagorese Stelling Stap 2

2. Ken die veranderlikes a, b en c toe aan die sye van jou driehoek. In die Pythagoras-stelling verwys die veranderlikes a en b na die regte sye van jou driehoek, en die veranderlike c na die skuinssy – die lang sy teenoor die regte hoek. So om mee te begin ken jy die veranderlikes a en b (die volgorde maak nie saak nie) toe aan die reguit sye en jy ken c aan die skuinssy.

Prent getiteld Gebruik die Pythagorese Stelling Stap 3

3. Bepaal watter sy van die driehoek jy wil weet. Die Pythagoras-stelling laat jou toe om die lengte van enige sy van `n driehoek te vind, mits twee van die sye bekend is. Bepaal watter van die sye `n onbekende lengte het--a, b, en/ofc. As net een onbekend is, dan kan jy aanbeweeg.

Gestel ons weet dat die skuinssy `n lengte van 5 het en een van die ander sye `n lengte van 3. Die lengte van die oorblywende sy is onbekend. Aangesien twee van die sye bekend is, kan ons voortgaan om die lengte van die onbekende sy te bereken! Ons sal hierdie voorbeeld later weer gebruik.

As die lengte van twee van die sye onbekend is, dan moet jy die lengte van ten minste nog een sy bepaal om die Pythagoras-stelling te kan gebruik. Die basiese trigonometriese funksies kan jou hiermee help, mits jy een van die ander nie-regte hoeke van die driehoek ken.

Prent getiteld Gebruik die Pythagorese Stelling Stap 4

4. Bereken deur die vergelyking en die bekendes te gebruik. Voeg die waardes vir die lengtes van die sye van jou driehoek in die vergelyking a + b = c. Onthou dat a en b die reguit sye is en c die skuinssy is.

In ons voorbeeld ken ons die lengte van een sy en dié van die skuinssy (3 & 5), dus skryf ons ons vergelyking soos volg: 3² + b² = 5²

Prent getiteld Gebruik die Pythagorese Stelling Stap 5

5. Bereken die vierkante. Om jou vergelyking op te los, begin deur elkeen van die bekende sye te kwadraeer. As jy dit makliker vind, kan jy die krag los en dit later vierkantig.

In ons voorbeeld vier ons 3 en 5 om resp. 9 en 25 om te kry. Ons kan nou die vergelyking herskryf as 9 + b² = 25.

Prent getiteld Gebruik die Pythagoras-stelling Stap 6

6. Isoleer die onbekende veranderlike aan die een kant van die gelykheidsteken. Gebruik opsioneel standaard algebraïese bewerkings om die onbekende aan die een kant van die gelykteken te kry en die vierkante aan die ander kant. As jy die skuinssy probeer vind, dan is c reeds in die posisie aan die een kant, so jy kan daardie stap oorslaan.

In ons voorbeeld is die vergelyking nou 9 + b² = 25. aan b² ons trek 9 van beide kante van die vergelyking af. Dit laat ons met b² = 16.

Prent getiteld Gebruik die Pythagoras-stelling Stap 7

7. Neem die vierkantswortel van beide kante van die vergelyking. Jy behoort nou `n vierkant (veranderlike) aan die een kant van die vergelyking te hê en `n getal aan die ander kant. Trek nou die vierkantswortel van albei kante af om die lengte van die onbekende te vind.

In ons voorbeeld, b² = 16, is die vergelyking na vierkantswortels b = 4. Ons kan dus sê dat die lengte van die onbekende sy van ons driehoek gelyk is aan 4.

Prent getiteld Gebruik die Pythagorese Stelling Stap 8

8. Gebruik die Pythagoras-stelling in die praktyk. Die rede waarom die Pythagoras-stelling so baie gebruik word, is omdat dit van toepassing is op die oplossing van baie praktiese probleme. Leer om reghoekige driehoeke in die wêreld om jou te herken – waar jy ook al `n reghoekige driehoek met een of meer voorwerpe kan identifiseer, kan die Pythagoras-stelling gebruik word om die lengte van een van die sye te vind, mits daar twee sye of hoeke is.

Kom ons neem `n voorbeeld uit die werklike wêreld. `n Leer leun teen `n muur. Die onderkant van die leer is 5 meter van die muur af. Die leer kom tot 20 meter gemeet vanaf die onderkant van die muur. Hoe lank is die leer?

"5 meter is die afstand na die muur” en "die leer is 20 meter hoog”. Dit gee `n aanduiding van die lengte van die sye van die driehoek. Aangesien die muur en die grond veronderstel is om `n regte hoek te vorm en die leer teen `n hoek skuins met die muur is, kan ons hierdie rangskikking as `n reghoekige driehoek beskou, waarvan die sye `n lengte van a = 5 en b = 20 het. Die lengte van die leer is die skuinssy, die onbekende veranderlike c. Kom ons pas die Pythagoras-stelling hier toe:

a² + b² = c²

(5)² + (20)² = c²

25 + 400 = c²

425 = c²

sqrt(425) = c

c = 20,6 . Die lengte van die leer is (ongeveer) 20,6 meter.

Metode 2 van 2: Bereken die afstand tussen twee punte in die vlak

Prent getiteld Gebruik die Pythagoras-stelling Stap 9

1. Definieer twee punte in die vlak. Die Pythagoras-stelling kan baie maklik gebruik word om die afstand in `n reguit lyn tussen twee punte in die vlak te bepaal. Al wat jy nodig het, is die x- en y-koördinate van enige twee punte. Gewoonlik word hierdie koördinate geskryf as (x, y).

Om die afstand tussen hierdie twee punte te vind, beskou ons elkeen van die punte as een van die hoekpunte van `n regte driehoek, wat nie aan die regte hoek behoort nie. Dit maak dit baie maklik om die lengte van a en b te vind, waarna c (die skuinssy en die afstand tussen die twee punte) bereken kan word.

Prent getiteld Gebruik die Pythagoras-stelling Stap 10

2. Teken die twee punte op `n grafiek. In `n X-Y-vlak, vir elke punt (x, y), is x `n punt op die horisontale x-as en y is `n punt op die vertikale y-as. Jy kan die afstand tussen die twee vind sonder om hulle te teken, maar om dit te doen sal jou `n visuele verwysing gee om te kyk of jou antwoord sin maak.

Prent getiteld Gebruik die Pythagorese Stelling Stap 11

3. Vind die lengte van die reguit sye van jou driehoek. Deur jou twee punte te beskou as die hoeke van die driehoek langs die skuinssy, kan jy die lengtes van sye a en b vind. Jy kan dit doen deur die grafiek te gebruik, of deur die formules |x te gebruik₁ - X₂| vir die horisontale kant en |y₁ - y₂| vir die vertikale kant, waar (x₁,y₁) is die eerste punt en (x₂,y₂) die tweede punt.

Gestel ons het die punte (6.1) en (3.5). Die lengte van die horisontale sy van ons driehoek is:

|x₁ - X₂|

|3 - 6|

| -3 | = 3

Die lengte van die vertikale sy is:

|y₁ - y₂|

|1 - 5|

| -4 | = 4

Ons kan dus sê dat die lengte van die sye van ons regte driehoek gelyk is aan a = 3 en b = 4.

Prent getiteld Gebruik die Pythagorese Stelling Stap 12

4. Gebruik die Pythagoras-stelling om die skuinssy te vind. Die afstand tussen die twee punte is die lengte van die skuinssy van die driehoek. Gebruik die Pythagoras-stelling om die skuinssy van die driehoek met sye a, b en c te vind.

In ons voorbeeld ken ons die punte (3,5) en (6.1), en die lengtes van die sye is a= 3 en b=4, dus bepaal ons die skuinssy soos volg:

(3)²+(4)²= c²

c= sqrt(9+16)

c= sqrt(25)

c= 5. Die afstand tussen (3.5) en (6.1) is 5.

Wenke

As die driehoek nie `n reghoekige driehoek is nie, kan jy nie net die Pythagoras-stelling gebruik nie.
Die skuinssy is altyd:

die lyn oorkant die regte hoek
die langste sy van die regte driehoek
die veranderlike c in die Pythagoras-stelling

sqrt(x) beteken "die vierkantswortel van x".

Moenie vergeet om altyd jou antwoorde na te gaan nie. As dit lyk of `n antwoord nie reg is nie, gaan jou berekeninge na, of begin oor.

As jy net een sy van die driehoek ken, maar ook een van die ander hoeke (as die regte hoek), bereken eers `n ander sy deur wat jy weet van trigonometrie (sin, cos, tan) of die verhoudings 30-60- 90 / 45-45-90.

Nog `n kontrole – die langste kant is teen die grootste hoek en die kortste kant is teen die kleinste hoek.