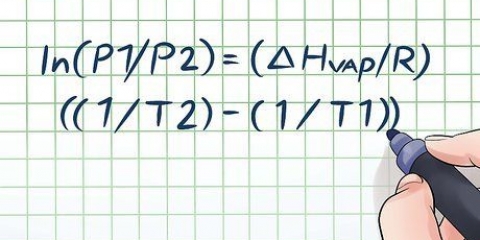Berekening van dryfvermoë: 12 stappe (met prente)

Inhoud

Trappe
- Metode 1 van 2: Gebruik die dryfkragvergelyking
- Metode 2 van 2: `n Eenvoudige dryfvermoë-eksperiment
Wenke
Benodigdhede

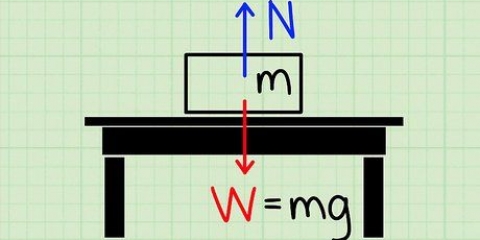
Die dryfkrag is die krag teenoor die swaartekrag op voorwerpe in `n vloeistof. Wanneer `n voorwerp in `n vloeistof geplaas word, druk die gewig van die voorwerp af op die vloeistof (vloeistof of gas) terwyl `n opwaartse krag teen die voorwerp opstoot, teen swaartekrag. Oor die algemeen kan hierdie dryfkrag met behulp van die vergelyking bereken word f_b = V_s × D × g, waar F_b die dryfkrag is, V_s die volume van die ondergedompelde deel van die voorwerp, D die digtheid van die vloeistof waarin die voorwerp ondergedompel is en g die swaartekrag. Om die dryfvermoë van `n voorwerp te bereken, kan jy verder lees hieronder by Stap 1.

Trappe

Metode 1 van 2: Gebruik die dryfkragvergelyking

Prent getiteld Bereken dryfvermoë Stap 1

1. Bepaal die volume van die onderwater deel van die voorwerp. Die dryfkrag op `n voorwerp is direk eweredig aan die volume van die voorwerp wat onder water is. Met ander woorde, hoe meer van `n voorwerp wat onder die water is, hoe groter is die dryfkrag wat daarop inwerk. Dit beteken dat selfs voorwerpe wat in vloeistof sink `n opwaartse krag het wat hulle opwaarts druk. Om die dryfkrag op `n voorwerp te bereken, is jou eerste stap gewoonlik om die volume van die voorwerp wat in `n vloeistof ondergedompel is, te bepaal. Vir die vergelyking van die dryfkrag moet hierdie waarde uitgedruk word in kubieke meter (m).

Vir voorwerpe wat heeltemal in die vloeistof ondergedompel is, is die volume water gelyk aan die volume van die voorwerp self. Vir voorwerpe wat in `n vloeistof dryf, word slegs die volume onder die vloeistof se oppervlak ingesluit.
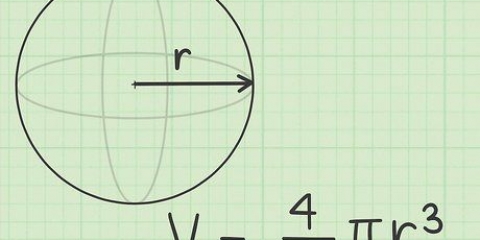
Byvoorbeeld, kom ons sê ons wil weet wat die dryfkrag is van `n rubberbal wat in water dryf. As die bal `n perfekte sfeer is met `n deursnee van 1 meter (3.3 voet) en presies halfpad deur die bal wat in die water dryf, dan kan ons die volume van die deel onder water vind deur die volume van die hele bal te bepaal, dan neem ons die helfte daarvan. Aangesien die volume van `n sfeer gelyk is aan (4/3)π(radius), weet ons dat die volume van die bal gelyk is aan (4/3)π(0.5) = 0,524 m. 0,524/2 = 0,262 m onder water.

Prent getiteld Bereken dryfvermoë Stap 2

2.Bepaal die digtheid van die vloeistof. Die volgende stap in die proses om die dryfkrag te bepaal, is om die digtheid (in kg/meter) van die vloeistof waarin die voorwerp gedompel is, te definieer. Digtheid is `n maatstaf van die gewig van `n voorwerp of stof relatief tot sy volume. Vir twee voorwerpe van gelyke volume sal die voorwerp met die hoër digtheid meer weeg. As `n reël, hoe hoër die digtheid van die vloeistof waarin `n voorwerp gedompel word, hoe groter is die dryfkrag. Vir vloeistowwe is dit oor die algemeen die maklikste om digtheid te bepaal bloot deur dit op te soek in die binas (of ander naslaanboek).

In ons voorbeeld dryf die bal in die water. Nadat ons `n naslaanboek geraadpleeg het, weet ons dat water `n digtheid van ongeveer het 1.000 kg/m.

Die digtheid van baie ander algemene vloeistowwe word in die binas (en ander naslaanwerke) gelys. U kan so `n lys raadpleeg via hierdie webwerf.

Prent getiteld Bereken dryfvermoë Stap 3

3. Bepaal swaartekrag (of ander afwaartse krag). Of `n voorwerp sink of in `n vloeistof dryf, dit is altyd onderhewig aan swaartekrag. In die werklike wêreld is hierdie konstante afwaartse krag gelyk aan 9,81 Newton/kg. In situasies waar ander kragte, soos die sentrifugale krag, egter ook op die vloeistof en die voorwerp wat daarin gedompel is inwerk, moet dit ook in ag geneem word wanneer die totale `afwaartse` krag vir die hele sisteem bepaal word.

In ons voorbeeld, as ons met `n eenvoudige statiese stelsel te doen het, kan ons aanvaar dat slegs die enigste afwaartse krag op die vloeistof en die onderwater voorwerp die standaard gravitasiekrag is: 9,81 Newton/kg.

Wat egter as ons bal in `n emmer water dryf wat teen groot spoed in `n horisontale sirkel rondgegooi word? In hierdie geval (met die veronderstelling dat die emmer vinnig genoeg gedraai word om seker te maak dat nie die water of die bal uitval nie), kan die `af`-krag in hierdie situasie afgelei word van die sentrifugale krag wat geskep word deur die emmer te swaai, en nie swaartekrag nie.

Prent getiteld Bereken dryfvermoë Stap 4

4. Vermenigvuldig volume × digtheid × swaartekrag. As die waardes vir die volume van die voorwerp (in m), die digtheid van die vloeistof (in kg/m) en die swaartekrag (of die afwaartse krag in die stelsel) gegee word, dan is die bepaling van die dryfkrag maklik. Vermenigvuldig net hierdie drie waardes om die dryfkrag in Newton te vind.

Kom ons los ons voorbeeldprobleem op deur hierdie waardes in die vergelyking F te koppel_b = V_s × D × g. f_b =0,262 m × 1 000 kg/m × 9,81 Newton/kg = 2 570 Newton.

Prent getiteld Bereken dryfvermoë Stap 5

5. Vind uit of jou voorwerp dryf (of in die water dryf) deur die dryfkrag met swaartekrag te vergelyk. Deur die dryfkragvergelyking te gebruik, is dit maklik om die krag te vind wat `n voorwerp opstoot uit die vloeistof waarin dit gedompel is. Met `n bietjie ekstra werk is dit egter ook moontlik om te bepaal of die voorwerp sal dryf of sink. Om dit te doen, bepaal die dryfkrag op die hele voorwerp (met ander woorde, neem die hele volume as V_s) en bepaal dan die swaartekrag wat die voorwerp afwaarts druk, deur die vergelyking G = (massa van voorwerp) (9.81 m/s) te gebruik. As die dryfkrag groter is as swaartekrag, sal die voorwerp dryf. Aan die ander kant sal dit sink as die swaartekrag groter is. As hulle gelyk is, kan jy sê dat die voorwerp in die vloeistof bly `sweef`.

Byvoorbeeld, kom ons sê ons wil weet of `n silindriese houtvat wat 20 kilogram weeg, 0,75 m in deursnee en 1,25 m hoog in water sal dryf. Dit vereis verskeie stappe:

Ons bepaal die volume met die formule vir die volume van `n silinder, V = π(radius)(hoogte). V = π(0,375)(1,25) = 0,55 meter.

Dan kan ons die dryfkrag op die vaartuig oplos (met standaard swaartekrag en water van gewone digtheid). 0,55 m × 1000 kg/m × 9,81 newton/kilogram = 5.395,5 N.

Nou moet ons die swaartekrag op die loop bepaal. G = (20 kg) (9,81 m/s) = 196,2 N. Dit is baie minder as die dryfkrag, so die loop sal op die water dryf.

Prent getiteld Bereken dryfvermoë Stap 6

6. Gebruik dieselfde benadering as vir `n vloeistof met `n gas. Wanneer jy vrae oor dryfvermoë uitwerk, moet jy in gedagte hou dat die vloeistof waarin die voorwerp gedompel is nie noodwendig `n vloeistof is nie. Gasse is ook basies vloeistowwe, en hoewel hulle `n baie lae digtheid het in vergelyking met ander stowwe, kan hulle steeds die gewig van sekere voorwerpe wat daarin dryf, dra. `n Eenvoudige heliumballon is `n duidelike bewys hiervan. Omdat die gas in die ballon minder dig is as die vloeistof om dit (gewone lug), dryf dit!

Metode 2 van 2: `n Eenvoudige dryfvermoë-eksperiment

Prent getiteld Bereken dryfvermoë Stap 7

1. Plaas `n klein bak of koppie in `n groter. Met `n paar huishoudelike items is dit maklik om die beginsels van dryfvermoë in aksie te sien! In hierdie eenvoudige eksperiment sal ons wys dat `n ondergedompelde voorwerp dryfkrag ervaar omdat dit `n hoeveelheid vloeistof gelykstaande aan die volume van die ondergedompelde voorwerp verplaas. Terwyl ons dit doen, sal ons jou ook wys hoe om die dryfkrag van `n voorwerp op `n praktiese manier met hierdie eksperiment te vind. Om te begin, plaas `n klein oop houer, soos `n bak of koppie, binne `n groter houer, soos `n groot bak of emmer.

Prent getiteld Bereken dryfvermoë Stap 8

2. Vul die binneste houer tot die rand. Vul nou die klein binnehouer met water. Maak seker dat jy dit tot op die rand vul sonder om te mors. Wees versigtig! As jy water mors, maak asseblief die groter houer leeg voordat jy weer probeer.

Vir die doel van hierdie eksperiment is dit veilig om aan te neem dat water `n standaarddigtheid van 1 het.000 kg/m. Tensy jy soutwater of `n heeltemal ander vloeistof gebruik, sal die meeste waters `n digtheid naby genoeg aan hierdie verwysingswaarde hê dat `n klein verskil nie ons resultate sal verander nie.

As jy `n pipet het, kan dit baie nuttig wees vir die korrekte herverspreiding van die water in die binneste houer.

Prent getiteld Bereken dryfvermoë Stap 9

3. Dompel `n klein voorwerp in die water. Soek nou ’n klein voorwerp wat in die binnehouer pas wat water kan weerstaan. Bepaal die massa van hierdie voorwerp in kilogram (jy kan `n skaal of balans gebruik wat sy gewig in gram aandui, en dit dan omskakel na kilogram). Doop dit dan stadig en eweredig onder die water totdat dit begin dryf of jy dit skaars kan vashou, waarna jy dit laat gaan. Van die water in die binneste houer sal oor die rand na die buitenste houer mors.

Vir die doel van ons voorbeeld, kom ons sê ons sit `n speelgoedmotor met `n massa van 0,05 kg in die binneste houer. Ons hoef nie die volume van die motor te bereken om die dryfkrag te bereken nie, soos ons in die volgende stap sal sien.

Prent getiteld Bereken dryfvermoë Stap 10

4. Gooi die oorlopende water in `n glas. Wanneer ons `n voorwerp in water dompel, word `n deel daarvan verplaas. As dit nie die geval was nie, sou daar geen ruimte wees vir die voorwerp om in die water te sink nie. Wanneer die water deur die voorwerp weggestoot word, stoot die water terug, wat dryfkrag tot gevolg het. Neem die water wat in die buitenste houer geloop het en gooi dit in `n klein maatbeker. Die hoeveelheid water in die maatbeker moet ongeveer gelyk wees aan die volume van die onderwater voorwerp.

Met ander woorde, as jou voorwerp dryf, is die volume van die gemorste water gelyk aan die volume van die voorwerp wat onder die oppervlak van die water is. As die voorwerp sink, sal die volume water wat gemors word gelyk wees aan die volume van die hele voorwerp.

Prent getiteld Bereken dryfvermoë Stap 11

5. Bereken die gewig van die gemorste water. Aangesien jy die digtheid van water ken en die volume van die gemorste water met die maatbeker kan meet, ken jy ook die massa. Skakel die volume om na m (a aanlyn omskakelingsinstrument nuttig) en vermenigvuldig dit met die digtheid van water (1.000 kg/m).

Gaan voort met ons voorbeeld, veronderstel ons speelgoedmotor het in die binneste houer gesink en ongeveer twee eetlepels water (0,00003 m) verplaas. Om die massa van die water te vind, vermenigvuldig ons dit met die digtheid: 1.000 kg/m × 0,00003 m = 0,03 kg.

Prent getiteld Bereken dryfvermoë Stap 12

6. Vergelyk die massa van die verplaasde water met dié van die voorwerp. Noudat jy die massa van beide die voorwerp wat in water ondergedompel is en dié van die verplaasde water ken, kan jy albei vergelyk om te sien watter een is groter. As die massa van die onderwater voorwerp groter is as dié van die verplaasde water, dan moes dit gesink het. Aan die ander kant, as die massa van die verplaasde water groter is, dan moes die voorwerp gedryf het. Dit is die beginsel van dryfkrag in aksie - om as `n voorwerp kop bo water te bly, sal dit `n massa water groter as dié van die voorwerp self moet verplaas.

Dus, lae massa maar hoë volume voorwerpe is die mees veerkragtige voorwerptipes. Hierdie eienskap beteken dat hol voorwerpe `n sterk dryfkrag ervaar. Dink aan `n kano - dit dryf goed omdat dit hol is, so `n kano kan baie water beweeg sonder `n baie hoë massa. As kano`s nie hol was nie, sou hulle nie baie goed gedryf het nie.

In ons voorbeeld het die motor `n groter massa (0,05 kg) as die verplaasde water (0,03 kg). Dit is in ooreenstemming met wat ons waargeneem het: die motor het gesink.