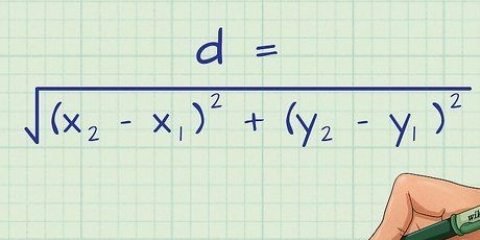Berekening van arbeid: 11 stappe (met prente)

Inhoud

Trappe
Wenke

In fisika, beteken "arbeid" iets heeltemal anders as alledaagse spraak. Om presies te wees, die term "arbeid" gebruik wanneer `n fisiese krag `n voorwerp laat beweeg. Oor die algemeen, hoe groter die verplasing deur `n gegewe krag, hoe meer werk word gedoen. Werk kan met die formule bereken word Werk = F × D × cos(θ), waar F = krag (in newton), D = verplasing (in meter) en θ = die hoek tussen die vektorkrag en die bewegingsrigting.

Trappe

Deel 1 van 3: Bepaling van arbeid in `n dimensie

1. Bepaal die rigting van die krag en die rigting van die beweging. Om mee te begin, is dit belangrik om beide die rigting van die krag en dié van die voorwerp te bepaal. Onthou dat voorwerpe nie altyd in dieselfde rigting beweeg as die krag wat op hulle toegepas word nie; byvoorbeeld, as jy `n klein karretjie aan die handvatsel trek, oefen jy `n diagonale krag daarop toe (as jy langer is as wat die wa hoog is) om dit vorentoe te beweeg. In hierdie afdeling handel ons oor situasies waar krag en beweging "wel" in dieselfde rigting gaan. Vir inligting oor hoe om arbeid so te bereken "nie" indien wel, kan jy hieronder meer lees.

Om dit duidelik te maak, sal ons die volgende probleem uitwerk. Gestel `n speelgoedtrein word deur `n lokomotief getrek. In hierdie geval is beide die kragvektor en die rigting van die trein se beweging gelyk aan mekaar; vorentoe. In die volgende paar stappe gebruik ons hierdie inligting om die werk verrig deur die lokomotief te bereken.

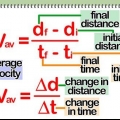
2. Bepaal die verplasing van die voorwerp. Die eerste veranderlike wat ons nodig het vir die formule van werk is D, of verplasing, wat gewoonlik maklik is om te vind. Verplasing is die afstand wat `n voorwerp in `n reguit lyn beweeg word. In wetenskaplike probleme word hierdie inligting gewoonlik gegee, of dit is moontlik om dit uit die data af te lei. In die regte wêreld kan jy die verplasing vind deur die afstand tussen die begin- en eindpunt te meet (nie langs die pad wat gereis is nie, maar "soos die kraai vlieg").

Die afstand moet in meter (SI-eenheid) vertoon word.

In ons voorbeeld van die trein bepaal ons die werk wat op die trein gedoen word terwyl dit langs die spoor beweeg. As die beginpunt op 0 gestel is, en die eindpunt op 2 meter, dan sê ons dat die verplasing D gelyk is aan 2 meter.

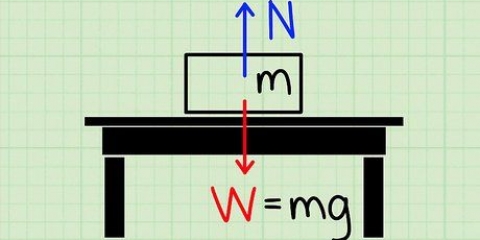
3. Bepaal die krag wat op die voorwerp uitgeoefen word. Bepaal dan die grootte van die krag wat gebruik word om die voorwerp te laat beweeg. Dit is `n maatstaf vir die "grootte" van die krag; hoe groter die krag, hoe groter sal die versnelling van die voorwerp wees. As die grootte van die krag nie gegee word nie, kan jy dit aflei van die massa en versnelling van die voorwerp (met die veronderstelling dat daar geen ander kragte is om in ag te neem nie) volgens die formule F = M xA.

Let daarop dat die eenheid van krag die Newton is.

Gestel ons weet nie die grootte van die krag in hierdie voorbeeld nie. Maar ons weet wel dat die massa van die trein gelyk is aan 0,5 kg en dat die krag dit teen 0,7 m/s laat versnel. In hierdie geval kan ons die grootte vind deur M x A = 0,5 x 0,7 = te gebruik 0,35 Newton.

4. Vermenigvuldig die krag maal die afstand. As jy weet wat die grootte van die krag op die voorwerp is en die afstand wat dit beweeg het, is die res maklik. Vermenigvuldig hierdie twee waardes saam om die werk te vind.

Nou is dit tyd om die werklike probleem op te los. Met `n waarde vir die krag van 0,35 Newton en `n waarde vir die verplasing van 2 meter, word die antwoord: 0,35 × 2 = 0,7 joule.

Jy het dalk opgemerk dat in die formule soos in die inleiding aangedui, daar een bykomende deel is: cos(θ). Soos hierbo genoem, is die krag en rigting van die beweging dieselfde. Dit beteken dat die hoek tussen hulle gelyk is aan 0. Aangesien cos(0) = 1, het ons nie die hoek nodig nie, want dit is gelyk aan 1.

5. Gee die antwoord in joules. In fisika, o.a. arbeid byna altyd uitgedruk in joules. 1 Joule word gedefinieer as 1 Newton wat op 1 meter uitgeoefen word, of met ander woorde, 1 Newton × meter. Dit lyk logies omdat jy `n afstand met krag vermenigvuldig en dit dus in Nm uitdruk.

Let daarop dat daar `n alternatiewe uitdrukking vir joules is; 1 Watt per sekonde. Sien hieronder vir `n meer gedetailleerde behandeling van mag met betrekking tot werk.

Deel 2 van 3: Vind werk wanneer krag vanuit `n hoek toegepas word

1. Bepaal die krag en verplasing soos gewoonlik. Hierbo het ons `n probleem oor werk bespreek, waar die voorwerp en die krag in dieselfde rigting gaan. In werklikheid is dit dikwels nie die geval nie. In daardie gevalle waar die krag op en die beweging van die voorwerp teenoorgesteld is, moet jy die verskil tussen die twee in ag neem en dit by die berekening insluit vir die korrekte resultaat. Om te begin, vind die grootte van die krag en die verplasing van die voorwerp soos gewoonlik.

Kom ons kyk na `n ander voorbeeld. In hierdie geval, kom ons sê ons trek die trein net soos in die vorige voorbeeld, maar die trek is opwaarts gehoek. Ons sal dit in die volgende stap in ag neem, maar vir eers hou ons by die basiese beginsels: die verplasing van die trein en die grootte van die krag op die trein. Gestel die krag het `n grootte van 10 newton en dat die verplasing weer gelyk is aan 2 meter, soos voorheen.

2. Bepaal nou die hoek tussen die rigting van die krag en die verplasing. Anders as die voorbeelde hierbo beskryf, is dit nou nodig om die verskil tussen die twee rigtings, uitgedruk in die hoek, te bepaal. As hierdie data nie gegee word nie, kan jy dit meet of dit aflei van ander inligting wat jy wel het.

In ons voorbeeldprobleem sê ons dat die krag vanuit `n hoek van 60 grade vanaf die horisontaal toegepas word. As die trein steeds horisontaal beweeg, dan is die hoek tussen die trein se verplasing en die krag gelyk aan 60.

3. Vermenigvuldig die krag F maal die verplasing D maal die hoek cos(θ). Sodra jy die verplasing, die krag en die hoek (tussen vektor en beweging) ken, is die oplossing amper so maklik soos dit is sonder om die hoek in ag te neem. Neem net die cos van die hoek (jy sal waarskynlik `n sakrekenaar hiervoor nodig hê) en vermenigvuldig dit met die krag en verplasing om jou antwoord te vind (in joules).

Kom ons los nou die voorbeeldprobleem op. Met behulp van `n sakrekenaar bepaal ons dat cos 60 gelyk is aan 1/2. Vul dit in die formule en dan kan ons oplos: 10 Newton × 2 meter × 1/2 = 10 joule.

Deel 3 van 3: Gebruik `n waarde vir arbeid

1. Jy kan ook die formule omkeer om die afstand, krag of hoek te vind. Die formule hierbo gegee is natuurlik nie net nuttig om werk te kry nie, maar ook, indien dit werk gegee word, om die ander veranderlikes van dieselfde formule te vind. In hierdie gevalle isoleer jy net die veranderlike wat jy wil bereken en oplos volgens eenvoudige algebraïese beginsels.

Gestel met die wete dat die trein met `n krag van 20 Newton teen `n hoek getrek word, en langs die spoor beweeg vir `n afstand van 5 meter, wat 86,6 Joule werk doen. Maar ons weet nie die hoek waarteen die krag op die voorwerp inwerk nie. Om dit op te los, kom ons plaas die veranderlike apart en werk dit so uit:
86,6 = 20 × 5 × cos(θ)
86,6/100 = cos(θ)
arccos(0.866) = θ = 30

2. Deel deur die tyd wat dit geneem het om die vermoë te vind. Arbeid is direk verwant aan "krag". Krag is bloot `n manier om die hoeveelheid werk wat binne `n gegewe stelsel verrig is, uit te druk oor die tyd wat dit geneem het. Dus, om die krag te vind, hoef jy net die werk te doen om die voorwerp te skuif, deur die tydsduur van die skuif te deel. Drywing word uitgedruk in eenhede van Watt (gelyk aan Joules per sekonde).

Gestel, gebaseer op die voorbeeld hierbo, het dit 12 sekondes geneem om die trein 5 meter te beweeg. In daardie geval deel ons die werk gedoen (86,6 joule) deur die tyd (12 sekondes) om die antwoord te vind. Die krag is dus: 86.6/12 = `7.22 watt.

3. Gebruik die formule TME_i + W_nc = TME_f om die meganiese energie van `n sisteem te vind. Werk kan ook gebruik word om die energie van `n gegewe sisteem te bepaal. In die bogenoemde formule, TME_i = is die aanvanklike totale meganiese energie binne die stelsel, TME_f = die finaal totale meganiese energie binne die sisteem, en W_nc = die werk wat op die sisteem gedoen word as gevolg van nie-konserwatiewe kragte.. In hierdie formule, as die krag beweeg met die rigting van verplasing, dan is dit positief, en as dit teenstaan, is dit negatief. Let daarop dat beide veranderlikes van energie gevind kan word met die formule (½)mv waar m = massa en v = volume.

Byvoorbeeld, in die voorbeeldprobleem twee stappe vroeër, kan ons aanneem dat die trein in beginsel `n totale meganiese energie van 100 joule gehad het. Aangesien die krag die trein in hierdie voorbeeld in die rigting van beweging trek, is dit positief. Die energie van die trein is TME_i + W_nc = 100 + 86,6 = 186, joule.

Let daarop dat nie-konserwatiewe kragte daardie kragte is waar die krag wat nodig is om `n voorwerp te versnel afhang van die voorwerp se pad. Wrywing is `n goeie voorbeeld; `n voorwerp wat `n kort reguit pad na `n sekere punt gedruk word, sal gemiddeld minder wrywing ervaar as `n voorwerp wat `n langer kronkelende pad na dieselfde eindpunt as die kort pad gedruk het.

Wenke

As jy dit regkry om `n probleem op te los, glimlag en klop jouself op die skouer!
Werk soveel moontlik oefeninge uit waarmee jy die onderwerp leer verstaan.
Hou aan oefen en probeer weer as dit nie die eerste keer werk nie.
Leer die volgende punte oor arbeid:

Arbeid kan positief of negatief wees. (Hier bedoel ons die fisiese betekenis van positief en negatief, nie die letterlike betekenis nie.)
Werk is negatief as die krag teenoor die rigting van verplasing is.
Werk is positief as die krag gelyk is aan die rigting van verplasing.

Artikels oor die onderwerp "Bereken arbeid"

Bereken versnelling

Bereken verplasing

Bereken die spoed van 'n voorwerp

Bereken massa

Оцените, пожалуйста статью