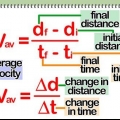
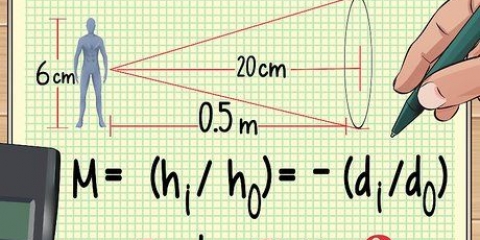
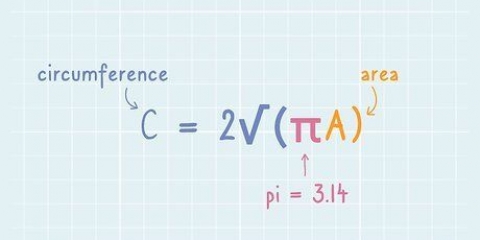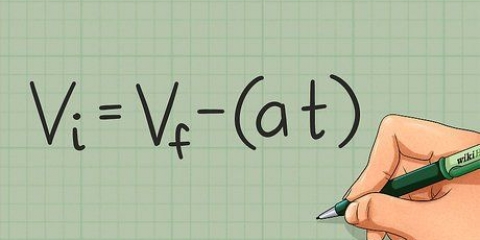Verplasing = d Verplasing is die afstand wat `n gegewe voorwerp afgelê het. Gewoonlik word die eenheid van verplasing in meter aangeteken. Tyd = t Spoed = v Vektoriale snelheid is die spoed van `n voorwerp in `n bepaalde rigting. Wanneer oombliklike spoed bereken word, soek ons die spoed van `n voorwerp op `n gegewe oomblik t (tyd). Snelheid word gewoonlik in meter per sekonde (m/s) aangeteken. Helling (of "gradiënt") = m Dit kan nuttig wees om die beweging van `n voorwerp in `n eenvoudige x-y-grafiek te wys met tyd langs die x-as en verplasing langs die y-as. Dan is die helling van die lyn by `n sekere punt die spoed van die voorwerp. 
Die snelheid (v) op `n gegewe tyd (t) is gelyk aan die helling (tempo van verandering) van bogenoemde vergelyking, waar verplasing (d) teen tyd (t) geplot word. 
`n Algemene reël vir die vind van die afgeleide: As y = a*x, dan is die afgeleide a*n*x. Hierdie reël word op enige term van die polinoom toegepas. Die konstante (die getal sonder `n veranderlike langsaan) sal verdwyn omdat dit met 0 vermenigvuldig word. 






Om oombliklike snelheid te bereken is dit nodig om die helling van `n grafiek vir enige gegewe punt te bereken. 




Die waarde waartoe die helling beweeg as H 0 nader, is die limiet. Dit is gelyk aan die helling van die raaklyn aan die kromme. Die raaklyn is `n reguit lyn wat gedefinieer word as `n parallel met die parabool oor `n oneindig kort afstand. Die helling van die raaklyn is dus die helling van die parabool/kromme as H `n oneindige afstand op die lyn word. Die vergelyking vir die vind van die raaklyn is die afgeleide van die vergelyking van die verplasingsfunksie, soos in deel een. 
Bereken oombliklike spoed
Inhoud
Vektoriale spoed (snelheid in Engels) word gedefinieer as die spoed van `n voorwerp in `n bepaalde rigting. Vir algemene doeleindes is die vind van die spoed van `n voorwerp so eenvoudig soos om die afstand afgelê te deel deur die tyd wat dit neem om daardie afstand te reis. Maar dit gee slegs die gemiddelde spoed langs `n gegewe pad. Met behulp van wiskundige vergelykings en afgeleides is dit moontlik om die snelheid van die voorwerp op enige gegewe tyd langs die pad te bereken. Dit word genoem oombliklike spoed. Ter wille van gerief en leesbaarheid sal ons in die volgende na spoed verwys, beide wanneer ons `normale` spoed en vektoriese spoed bedoel.
Trappe
Metode 1 van 2: Berekening van die oombliklike spoed

1. Wat is "oombliklike spoed". Voorwerpe wat beweeg kan dit doen met a konstante spoed – wat teen `n konstante spoed deur die reis beweeg. `n Hardloper wat langs `n sokkerveld draf, handhaaf omtrent dieselfde spoed oor die hele lengte van die veld. Voorwerpe kan ook beweeg met `n veranderlike spoed. Byvoorbeeld, `n motor wat langs `n pad met baie draaie ry, sal nie heeltyd dieselfde spoed hê nie – in die draaie neem die spoed af, net om weer op die reguit te verhoog.
- Oombliklike spoed is `n maatstaf van die spoed van `n voorwerp op enige tydstip. Byvoorbeeld, die oombliklike spoed van `n vuurpyl, presies een sekonde ná die aansteek van die dryfmiddel, is baie laer as sy oombliklike spoed 30 sekondes ná opstyg, as die vuurpyl tyd gehad het om spoed te kry.

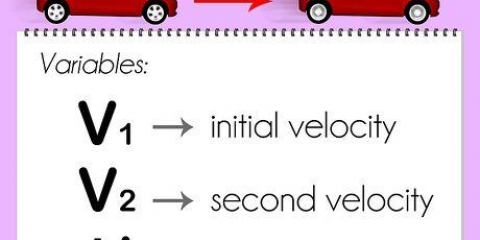
2. Ken jou veranderlikes. Wanneer jy te doen het met oombliklike snelheidsberekeninge, sal jy byna altyd sekere veranderlikes op `n sekere punt teëkom. Hierdie veranderlikes is:

3. N voorbeeld. Kom ons sê die verplasing van `n voorwerp kan deur `n vergelyking voorgestel word: verplasing(e) = 3t + 4t + 7. Die grafiek van hierdie funksie is `n geboë lyn of parabool, waar die x-as tyd voorstel en die y-as verplasing verteenwoordig.

4. Om die oombliklike snelheid van `n voorwerp met `n verplasing volgens bogenoemde funksie te bereken, benodig ons die afgeleide van hierdie funksie. Die afgeleide van `n funksie is gelyk aan die helling van die funksie by enige punt op die grafiek. Om die afgeleide te vind, differensieer ons die funksie volgens hierdie formule:

5. Gebruik hierdie formule om die afgeleide van die funksie te bereken. As ons dit skryf as y = 3x + 4x + 7, dan is die afgeleide (3*2)*x+(4*1)*x+(7*0)*x

6. Vereenvoudig die vergelyking. Deur al die terme tussen hakies te vermenigvuldig gee 6x+ 4x+ 0x

7. Hou aan om te vereenvoudig. Hierdie vergelyking kan geskryf word as 6x + 4. Die "0x" term word dan gelyk aan 0, terwyl die "4x" term word vereenvoudig tot 4 (n = 1.)

8. Maak hierdie nuwe funksie gelyk aan die helling m. Ons gebruik hierdie afgeleide funksie om die helling van die oorspronklike vergelyking te vind y = 3x + 4x + 7 vir enige gegewe waarde van x (tyd). Die oorspronklike helling van die vergelyking op enige gegewe tydstip is die oombliklike snelheid.

9. Vind die oombliklike spoed van die voorwerp vir t=4 sekondes. Al wat jy hoef te doen is om die tydwaarde in die x-veranderlike van die afgeleide van die vergelyking in te voer. Dit gee die volgende vergelyking y = 6(4) + 4 . Dit is vereenvoudig tot 28. Die oombliklike spoed van die voorwerp vir t=4 sekondes is 28 m/s.
Metode 2 van 2: Verstaan `n afgeleide

1. Teken `n gewone x-y-koördinaatstelsel. Om behoorlik te verstaan hoe `n afgeleide kan help om die oombliklike snelheid van `n voorwerp te vind, is `n grafiese voorstelling baie nuttig. Die y-as verteenwoordig die voorwerp se verplasing, terwyl die x-as tyd verteenwoordig.
- Die grafiek kan onder die x-as voortgaan. As die lyn wat die voorwerp se beweging voorstel onder die x-as daal, beteken dit die voorwerp beweeg in die omgekeerde rigting en voor die beginpunt. Gewoonlik sal die grafiek nie verder as die y-as strek nie. Spoed word nie gemeet vir voorwerpe wat terugbeweeg in tyd nie!
- As jy nie seker is hoe om `n grafiek te teken of presies wat die x-as en y-as verteenwoordig nie, leer hoe om kan `n grafiek van `n funksie teken.

2. Trek `n geboë lyn, begin vanaf die punt op die lyn x=0, in die rigting van die x-as. Die helling van die lyn is die tempo waarteen y verander gedeel deur die tempo waarteen x verander. Dus, as y gelyk is aan verplasing en x is gelyk aan tyd, dan is helling gelyk aan snelheid.

3. Om die helling van `n lyn vir `n sekere punt te vind, gebruik ons `n truuk waar ons die limiet van die vergelyking vind. Om die limiet te vind, vereis twee punte P en Q op `n geboë lyn en om die helling van die lyn deur beide punte te vind soos die afstand tussen die twee punte kleiner en kleiner word.

4. Kies `n punt P op die lyn. Plaas P byvoorbeeld op x=1. Die presiese ligging maak nie saak nie. Kies `n waarde wat gerieflik is.

5. Kies `n tweede punt Q op die lyn. Q moet `n entjie van die P af wees. In ons voorbeeld is Q by die punt met x=3, terwyl P by die punt is met x=1.

6. Vind die helling tussen P en Q. Die helling tussen P en Q word dan (die verskil in y-waarde van P en Q)/(die verskil in x-waarde P en Q). Ons verwys na hierdie verskil in x-waardes van P en Q as H. In hierdie geval is H gelyk aan 3-1=2.

7. Maak die waarde van H kleiner. Met ander woorde, bring Q nader aan P op die x-as, en bereken dan weer die helling tussen P en Q. Doen dit herhaaldelik en verminder elke keer die afstand tussen P en Q. Nadat dit `n paar keer bereken is, behoort dit duidelik te word dat die helling `n sekere waarde nader. Solank as wat H>0 sal die helling nooit hierdie waarde bereik nie, maar slegs nader. Ons sê dan dat die helling die limiet nader.

8. Gebruik afgeleides om die helling te vind as H `n oneindig klein interval op die lyn voorstel. Die afgeleide van `n vergelyking word gevind deur "x, is N*x" van toepassing op enige term van die oorspronklike vergelyking.
Wenke
- Verplasing is soos afstand, maar in `n sekere rigting, so verplasing is `n vektor en snelheid is `n skalêre hoeveelheid. Verplasing kan negatief wees terwyl afstand net positief kan wees.
- Om die versnelling (die verandering van snelheid oor tyd) te vind, gebruik die metode in deel een om die afgeleide van jou verplasingsfunksie te vind. Neem dan die afgeleide daarvan. Dit gee jou dan die vergelyking om die versnelling op enige gegewe tydstip te vind - al wat jy hoef te doen is om die tydwaarde in hierdie tweede afgeleide in te voer.
- Die vergelyking wat y (verplasing) met x (tyd) in verband bring kan baie eenvoudig wees, soos bv. y= 6x + 3. In hierdie geval is die helling konstant en dit is nie nodig om `n afgeleide van die helling te vind nie. Dit is gelyk aan 6, volgens die lineêre vergelyking y = mx + b.
Artikels oor die onderwerp "Bereken oombliklike spoed"
Оцените, пожалуйста статью
Gewilde