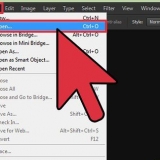
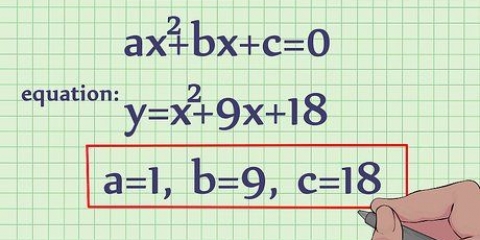3(x - 2/3) =
3(x - 2/3)(x -2/3) = 3[(x -2/3x -2/3x + 4/9)] 3 (x - 4/3x + 4/9) 
-4/3 + 15/3 = 11/3.










Split square
Inhoud
Kwadratering is `n nuttige tegniek om `n kwadratiese vergelyking te herskryf wat dit makliker maak om toesig te hou en op te los. Jy kan `n vierkant herskryf deur dit in meer hanteerbare stukke te herrangskik.
Trappe
Metode 1 van 2: Deel Een: Herskryf van `n standaardvergelyking

1. Skryf die vergelyking. Kom ons neem aan jy wil die volgende vergelyking oplos: 3x - 4x + 5.

2. Verwyder die koëffisiënt uit die vergelyking. Plaas die 3 buitehakies en deel elke term behalwe die konstante met 3. 3x gedeel deur 3 is x en 4x gedeel deur 3 is 4/3x. Die nuwe vergelyking lyk dus so: 3(x - 4/3x) + 5. Die 5 is buite die hakies omdat jy dit nie deur 3 gedeel het nie.

3. Deel die tweede term deur 2 en vierkantig. Die tweede term, ook genoem die b-term in die vergelyking, is 4/3. Halveer die tweede kwartaal. 4/3 ÷ 2, of 4/3 x 1/2, is gelyk aan 2/3. Kwadreer hierdie term deur beide die teller en noemer met hulself te vermenigvuldig. (2/3) = 4/9. Skryf hierdie term neer.

4. Optelling en aftrekking. jy het dit"bykomende" term wat nodig is om die eerste drie terme van die vergelyking in `n vierkant om te skakel. Maar onthou dat jy hierdie term bygevoeg het deur dit ook van die vergelyking af te trek. Dit maak natuurlik min verskil om die terme bloot weer te kombineer – dan is jy terug waar jy begin het. Die nuwe vergelyking moet nou so lyk: 3( x - 4/3 x + 4/9 - 4/9) + 5.

5. Kry die term wat jy afgetrek het buite hakies. Omdat jy reeds met die 3 buite die hakies werk, is dit nie moontlik om net -4/9 buite die hakies te plaas nie. Eerstens moet jy dit met 3 vermenigvuldig. -4/9 x 3 = -12/9, of -4/3. As jy te doen het met `n vergelyking wat slegs `n koëffisiënt 1 ofx bevat, kan jy hierdie stap oorslaan.

6. Skakel die terme tussen hakies om in `n vierkant. Jou vergelyking lyk nou so: 3(x -4/3x +4/9). Jy het van voor tot agter gewerk om 4/9 te kry, wat eintlik nog `n manier is om die faktor te vind wat die vierkant voltooi. So jy kan hierdie terme herskryf as: 3(x - 2/3). Jy kan dit kontroleer deur te vermenigvuldig waar jy sal sien dat jy weer dieselfde oorspronklike vergelyking as die antwoord kry.


7. Voeg die konstantes saam. Jy het nou twee konstantes, 3(x - 2/3) - 4/3 + 5. Al wat jy nou moet doen is om -4/3 by 5 by te tel en dit gee 11/3 as die antwoord. Jy doen dit deur hulle dieselfde noemer te gee: -4/3 en 15/3, en dan albei tellers by te tel om 11 te kry, en die noemer gelyk aan 3 te hou.


8. Skryf die vergelyking in `n ander vorm. Nou is jy klaar. Die finale vergelyking is 3(x - 2/3) + 11/3. Jy kan die 3 uitskakel deur die vergelyking deur 3 te deel, wat jou met die volgende vergelyking laat:(x - 2/3) + 11/9.Jy het nou suksesvol die vergelyking in `n ander vorm geskryf: a( x - h ) + k, waardeur k die konstante is.
Metode 2 van 2: Deel Twee: Los `n kwadratiese vergelyking op

1. Let op die taak. Kom ons neem aan jy wil die volgende vergelyking oplos: 3x + 4x + 5 = 6

2. Voeg die konstantes bymekaar en plaas dit aan die linkerkant van die gelykheidsteken. Konstante terme is daardie terme sonder `n veranderlike. In hierdie geval het jy 5 aan die linkerkant en 6 aan die regterkant. Jy wil 6 na links skuif, trek dus 6 van beide kante van die vergelyking af. Dit laat 0 aan die regterkant (6-6) en -1 aan die linkerkant (5-6). Die vergelyking lyk nou so: 3x + 4x - 1 = 0.

3. Neem die koëffisiënt van die vierkant buite die hakies. In hierdie geval is 3 die koëffisiënt van x. Om 3 van hakies uit te sluit, verwyder die 3, plaas die oorblywende term tussen hakies en deel elke term deur 3. Dus, 3x ÷ 3 = x, 4x ÷ 3 = 4/3x, en 1 ÷ 3 = 1/3. Die vergelyking lyk nou so: 3(x + 4/3x - 1/3) = 0.

4. Deel deur die konstante wat jy sopas tussen hakies geplaas het. Hiermee raak jy uiteindelik ontslae van daardie irriterende 3 buite die hakies. Deur elke term deur 3 te deel, kan dit uitgeskakel word sonder om die vergelyking te verander. Nou het jy: x + 4/3x - 1/3 = 0

5. Deel die tweede term deur 2 en vierkantig. Neem nou die tweede kwartaal, 4/3, de b term, en deel deur 2. 4/3 2 of 4/3 x 1/2, is 4/6, of 2/3. En 2/3 kwadraat is 4/9. Wanneer jy hiermee klaar is, moet jy dit links en regs van die vergelyking skryf, want jy het basies net `n nuwe term bygevoeg. Jy moet dit aan beide kante van die vergelyking doen. Die vergelyking lyk nou so: x + 4/3 x + 2/3 - 1/3 = 2/3

6. Skuif die oorspronklike konstante na die regterkant van die vergelyking en voeg dit by die term wat reeds daar is. Skuif die konstante, -1/3, na regs om dit 1/3 te maak. Voeg dit by die ander term, 4/9, of 2/3. Vind die kleinste gemene veelvoud sodat 1/3 en 4/9 bymekaar getel kan word. Dit gaan soos volg: 1/3 x 3/3 = 3/9. Tel nou 3/9 by 4/9 by sodat jy 7/9 aan die regterkant van die vergelyking het. Dit gee: x + 4/3 x + 2/3 = 4/9 + 1/3 en dan x + 4/3 x + 2/3 = 7/9.

7. Skryf die linkerkant van die vergelyking as `n vierkant. Aangesien jy reeds `n formule gebruik het om die ontbrekende term te vind, is die moeilikste deel reeds gedoen. Al wat jy hoef te doen is om die x en die helfte van die tweede koëffisiënt tussen hakies te plaas en dit te vierkantig, so :(x + 2/3). Let daarop dat die faktorisering van die vierkant 3 terme lewer: x + 4/3 x + 4/9. Die vergelyking lyk nou so: (x + 2/3) = 7/9.

8. Neem die vierkantswortel van beide kante van die vergelyking. Aan die linkerkant van die vergelyking is die vierkantswortel van (x + 2/3) gelyk aan x + 2/3. Die regterkant gee +/- (√7)/3. Die vierkantswortel van die noemer 9 is 3, en die vierkantswortel van 7 is √7. Moenie vergeet om die +/- te skryf nie, want `n vierkantswortel van `n getal kan positief of negatief wees.

9. Sit die veranderlike opsy. Om die veranderlike x van die res te isoleer, skuif die konstante 2/3 na die regterkant van die vergelyking. Jy het nou twee moontlike antwoorde vir x:+/- (√7)/3 - 2/3. Hierdie is jou twee antwoorde. Jy kan dit so los of uitbrei oor die vierkantswortel, as jy gevra word vir `n antwoord sonder `n radikale.
Wenke
- Maak seker jy plaas die +/- op die regte plekke anders kry jy net een antwoord.
- Selfs al ken jy die vierkantswortelformule, kan dit nie skade doen om so nou en dan kwadratiese vergelykings te oefen of kwadratiese vergelykings uit te werk nie. Op hierdie manier weet jy vir seker dat jy weet hoe om dit te doen wanneer dit nodig is.
Artikels oor die onderwerp "Split square"
Оцените, пожалуйста статью
Gewilde