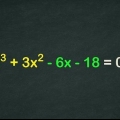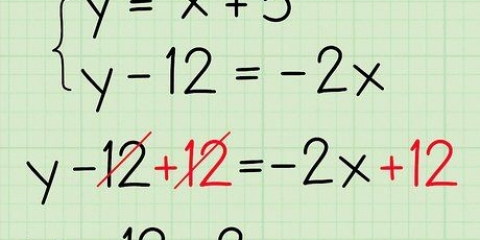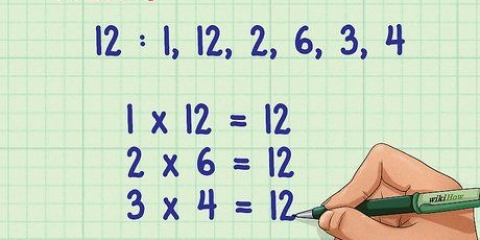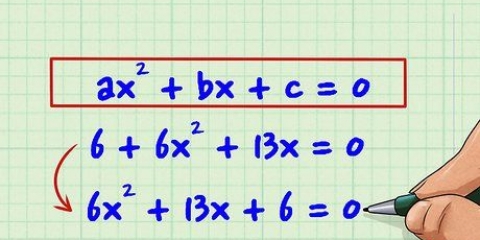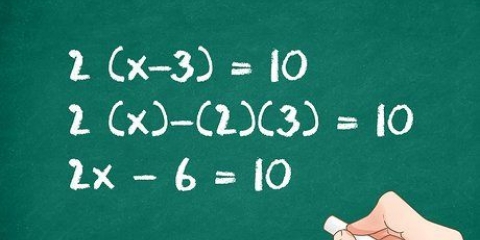Byvoorbeeld, 

Byvoorbeeld, om  in
in  om te isoleer, trek jy
om te isoleer, trek jy  van beide kante van die vergelyking af die vergelyking:
van beide kante van die vergelyking af die vergelyking:




Byvoorbeeld, om  om in opgelos te word
om in opgelos te word  , deel elke kant van die vergelyking deur
, deel elke kant van die vergelyking deur  :
:



So die oplossing van is is
is  .
. 

Byvoorbeeld, herskryf  so as
so as  .
. 
Byvoorbeeld,  .
. 
Byvoorbeeld, vir die kwadratiese polinoom  , jy moet twee getalle vind (
, jy moet twee getalle vind ( en
en  ), waar
), waar  en
en  .
. Omdat jy  jy weet dat een van die getalle negatief sal wees.
jy weet dat een van die getalle negatief sal wees. Jy behoort dit te sien  en
en  . So jy verdeel
. So jy verdeel  op in
op in  en herskryf die kwadratiese polinoom:
en herskryf die kwadratiese polinoom:  .
. 
Byvoorbeeld, die eerste twee terme in die polinoom  is
is  . `n Term wat in beide voorkom is
. `n Term wat in beide voorkom is  . Dit word die ontbinde groep
. Dit word die ontbinde groep  .
. 
Byvoorbeeld, die tweede twee terme in die polinoom  is
is  . `n Term wat in beide voorkom is
. `n Term wat in beide voorkom is  . So is die ontbinde groep
. So is die ontbinde groep  .
. 
Byvoorbeeld, na faktorisering deur groepering, word  gelyk aan
gelyk aan  .
. Die eerste binomiaal is  .
. Die tweede binomiaal is  .
. Dus die oorspronklike kwadratiese polinoom,  kan geskryf word as die gefaktoriseerde uitdrukking
kan geskryf word as die gefaktoriseerde uitdrukking  .
. 
Byvoorbeeld, om die eerste oplossing van te vind  , stel die eerste binomiale uitdrukking gelyk aan
, stel die eerste binomiale uitdrukking gelyk aan  en jou losmaak
en jou losmaak  aan. Dus:
aan. Dus:



Dus, die eerste oplossing van die kwadratiese polinoom is
is  .
. 
Byvoorbeeld, om die tweede oplossing vir te vind  , stel die tweede binomiale uitdrukking gelyk aan
, stel die tweede binomiale uitdrukking gelyk aan  en jou losmaak
en jou losmaak  aan. Dus:
aan. Dus:



Die tweede oplossing van die kwadratiese polinoom is dus gelyk aan
gelyk aan  .
.
Los polinome op
Inhoud
`n Polinoom is `n uitdrukking wat bestaan uit optelling en aftrekking van terme. `n Term kan bestaan uit veranderlikes, konstantes en koëffisiënte. Wanneer jy polinome oplos, probeer jy gewoonlik uitvind vir watter punte x = 0. Laagste graad polinome het een of twee oplossings, afhangende van of dit lineêre polinome of kwadratiese polinome is. Hierdie tipe polinome kan maklik opgelos word met behulp van elementêre algebra en faktorisering. Om hoërgraadpolinome op te los, kan jy artikels op wikiHow lees.
Trappe
Metode 1 van 2: Los `n lineêre polinoom op

1. Bepaal of jy met `n lineêre polinoom te doen het. `n Lineêre polinoom is `n polinoom van die eerste graad. Dit beteken dat geen veranderlike `n eksponent (of `n eksponent groter as 1) sal hê nie. Aangesien dit `n eerstegraadse polinoom is, het dit presies een oplossing.
- Byvoorbeeld,
is `n lineêre polinoom (of polinoom), omdat die veranderlike
het geen eksponent nie (wat dieselfde is as `n eksponent van 1).

2. Maak die vergelyking gelyk aan nul. Dit is `n noodsaaklike stap om alle polinome op te los.


3. Skuif die veranderlike term eenkant toe. Doen dit deur die konstante van beide kante van die vergelyking op te tel of af te trek. `n Konstante is `n term sonder `n veranderlike.
 in
in  om te isoleer, trek jy
om te isoleer, trek jy  van beide kante van die vergelyking af die vergelyking:
van beide kante van die vergelyking af die vergelyking:



4. Los die veranderlike op. Gewoonlik moet jy elke kant van die vergelyking deur die konstante deel. Dit gee jou die oplossing van die polinoom.
 om in opgelos te word
om in opgelos te word  , deel elke kant van die vergelyking deur
, deel elke kant van die vergelyking deur  :
:


So die oplossing van is
 is
is  .
.Metode 2 van 2: Los `n kwadratiese polinoom op

1. Bepaal of jy met `n kwadratiese polinoom te doen het. `n Kwadratiese polinoom is `n kwadratiese vergelyking. Dit beteken dat geen veranderlike `n eksponent groter as 2 het nie. Aangesien dit `n tweedegraadse polinoom is, is daar twee oplossings.
- Byvoorbeeld,
is `n kwadratiese polinoom, want die veranderlike
a
het as eksponent.

2. Maak seker dat die polinoom in volgorde van graad geskryf is. Dit beteken dat die term met eksponent  word eerste gelys gevolg deur die eerstegraadse term, dan die konstante.
word eerste gelys gevolg deur die eerstegraadse term, dan die konstante.
 word eerste gelys gevolg deur die eerstegraadse term, dan die konstante.
word eerste gelys gevolg deur die eerstegraadse term, dan die konstante. so as
so as  .
.
3. Maak die vergelyking gelyk aan nul. Dit is `n noodsaaklike stap om alle polinome op te los.
 .
.
4. Herskryf die uitdrukking as `n vierterm uitdrukking. Jy doen dit deur die eerstegraadse term (de  termyn). Jy soek twee getalle waarvan die som gelyk is aan die eerstegraadkoëffisiënt, en waarvan die produk gelyk is aan die konstante.
termyn). Jy soek twee getalle waarvan die som gelyk is aan die eerstegraadkoëffisiënt, en waarvan die produk gelyk is aan die konstante.
 termyn). Jy soek twee getalle waarvan die som gelyk is aan die eerstegraadkoëffisiënt, en waarvan die produk gelyk is aan die konstante.
termyn). Jy soek twee getalle waarvan die som gelyk is aan die eerstegraadkoëffisiënt, en waarvan die produk gelyk is aan die konstante. , jy moet twee getalle vind (
, jy moet twee getalle vind ( en
en  ), waar
), waar  en
en  .
. jy weet dat een van die getalle negatief sal wees.
jy weet dat een van die getalle negatief sal wees. en
en  . So jy verdeel
. So jy verdeel  op in
op in  en herskryf die kwadratiese polinoom:
en herskryf die kwadratiese polinoom:  .
.
5. Faktor deur groepering. Jy doen dit deur `n term te faktoriseer wat by die eerste twee voorwaardes in die polinoom pas.
 is
is  . `n Term wat in beide voorkom is
. `n Term wat in beide voorkom is  . Dit word die ontbinde groep
. Dit word die ontbinde groep  .
.
6. Faktoreer die tweede groep. Jy doen dit deur `n term wat in die tweede twee terme van die polinoom voorkom, te faktoriseer.
 is
is  . `n Term wat in beide voorkom is
. `n Term wat in beide voorkom is  . So is die ontbinde groep
. So is die ontbinde groep  .
.
7. Herskryf die polinoom as twee binomiale. `n Binomiaal is `n uitdrukking met twee terme. Jy het reeds `n binomiaal, die uitdrukking tussen hakies vir elke groep. Hierdie uitdrukking moet vir elke groep dieselfde wees. Die tweede binomiaal word gemaak deur die twee terme wat uit elke groep gefaktoreer is, te kombineer.
 gelyk aan
gelyk aan  .
. .
. .
. kan geskryf word as die gefaktoriseerde uitdrukking
kan geskryf word as die gefaktoriseerde uitdrukking  .
.
8. Vind eers die oplossing. Jy doen dit deur op te los  in die eerste binomiaal.
in die eerste binomiaal.
 in die eerste binomiaal.
in die eerste binomiaal. , stel die eerste binomiale uitdrukking gelyk aan
, stel die eerste binomiale uitdrukking gelyk aan  en jou losmaak
en jou losmaak  aan. Dus:
aan. Dus:


Dus, die eerste oplossing van die kwadratiese polinoom
 is
is  .
.
9. Bepaal die tweede oplossing. Jy doen dit deur  om in die tweede binomiaal op te los.
om in die tweede binomiaal op te los.
 om in die tweede binomiaal op te los.
om in die tweede binomiaal op te los. , stel die tweede binomiale uitdrukking gelyk aan
, stel die tweede binomiale uitdrukking gelyk aan  en jou losmaak
en jou losmaak  aan. Dus:
aan. Dus:


Die tweede oplossing van die kwadratiese polinoom is dus
 gelyk aan
gelyk aan  .
.Wenke
- Moenie bekommerd wees oor veranderlikes, soos t, of as jy `n vergelyking het wat gelykstaande is aan f(x) in plaas van 0. As die vraag wortels, nulle of faktore wil sien, hanteer dit soos enige ander probleem.
- Onthou die volgorde van bewerkings terwyl jy werk - maak eers die hakies skoon, doen dan die vermenigvuldiging en deling, en laastens optel en aftrek.
Artikels oor die onderwerp "Los polinome op"
Оцените, пожалуйста статью
Gewilde