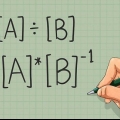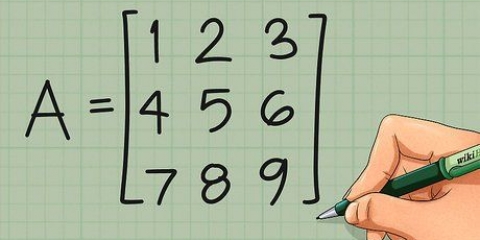Los matrikse op (met prente)

Inhoud

Trappe
Wenke

`n Matriks is `n baie nuttige manier om getalle in `n blokformaat voor te stel, wat jy dan kan gebruik om `n stelsel lineêre vergelykings op te los. As jy net twee veranderlikes het, sal jy waarskynlik `n ander metode gebruik. Lees hieroor in Oplos van `n stelsel vergelykings vir voorbeelde van hierdie ander metodes. Maar as jy drie of meer veranderlikes het, is `n matriks ideaal. Deur herhaalde kombinasies van vermenigvuldiging en optelling te gebruik, kan jy sistematies by `n oplossing uitkom.

Trappe

Deel 1 van 4: Stel die matriks op

1. Verifieer dat jy genoeg data het. Om `n unieke oplossing te kry vir elke veranderlike in `n lineêre stelsel deur `n matriks te gebruik, moet jy soveel vergelykings hê as die aantal veranderlikes wat jy probeer oplos. Byvoorbeeld: met die veranderlikes x, y en z benodig jy drie vergelykings. As jy vier veranderlikes het, het jy vier vergelykings nodig.

As jy minder vergelykings as die aantal veranderlikes het, sal jy `n paar grense van die veranderlikes leer (soos x = 3y en y = 2z), maar jy sal nie `n presiese oplossing kan kry nie. Vir hierdie artikel sal ons net werk aan `n unieke oplossing.

2. Skryf jou vergelykings in standaardvorm. Voordat jy data van die vergelykings in `n matriksvorm kan gooi, skryf jy eers elke vergelyking in standaardvorm. Die standaardvorm vir `n lineêre vergelyking is Ax+By+Cz=D, waar die hoofletters die koëffisiënte (syfers) is, en die laaste getal (in hierdie voorbeeld, die D) regs van die gelykheidsteken.

As jy meer veranderlikes het, gaan net voort met die lyn so lank as wat dit neem. Byvoorbeeld, as jy probeer om `n stelsel van ses veranderlikes op te los, sal jou standaardvorm soos Au+Bv+Cw+Dx+Ey+Fz=G lyk. In hierdie artikel sal ons fokus op stelsels met slegs drie veranderlikes. Om `n groter stelsel op te los is presies dieselfde, maar neem net meer tyd en meer stappe.

Let daarop dat in standaardvorm die bewerkings tussen die terme altyd `n byvoeging is. As daar `n aftrekking in jou vergelyking is, in plaas van `n optelling, sal jy later hiermee moet werk deur jou koëffisiënt negatief te maak. Om dit makliker te maak om te onthou, kan jy die vergelyking herskryf en die bewerking byvoeg en die koëffisiënt negatief maak. Byvoorbeeld, jy kan die vergelyking 3x-2y+4z=1 herskryf as 3x+(-2y)+4z=1.

3. Plaas die getalle van die stelsel vergelykings in `n matriks. `n Matriks is `n groep getalle, gerangskik in `n soort tabel, waarmee ons sal werk om die stelsel op te los. Dit bevat basies dieselfde data as die vergelykings self, maar in `n eenvoudiger formaat. Om die matriks van jou vergelykings in standaardvorm te maak, kopieer eenvoudig die koëffisiënte en die resultaat van elke vergelyking in `n enkele ry, en stapel daardie rye bo-op mekaar.

Gestel jy het `n stelsel wat bestaan uit die drie vergelykings 3x+y-z=9, 2x-2y+z=-3, en x+y+z=7. Die boonste ry van jou matriks sal die getalle 3, 1, -1, 9 bevat, aangesien dit die koëffisiënte en die oplossing van die eerste vergelyking is. Let daarop dat enige veranderlike wat nie `n koëffisiënt het nie, aanvaar word om `n koëffisiënt van 1 te hê. Die tweede ry van die matriks word 2, -2, 1, -3 en die derde ry 1, 1, 1, 7.

Maak seker dat jy die x-koëffisiënte in die eerste kolom, die y-koëffisiënte in die tweede, die z-koëffisiënte in die derde en die oplossingsterme in die vierde belyn. Wanneer jy klaar met die matriks gewerk het, sal hierdie kolomme belangrik wees wanneer jy jou oplossing skryf.

4. Trek `n groot vierkantige hakie om jou hele matriks. Volgens konvensie word `n matriks aangedui deur `n paar vierkantige hakies, [ ], rondom die hele blok getalle. Die hakies beïnvloed geensins die oplossing nie, maar dit dui wel aan dat jy met matrikse werk. `n Matriks kan uit enige aantal rye en kolomme bestaan. In hierdie artikel sal ons hakies om `n ry terme gebruik om aan te dui dat hulle bymekaar hoort.

5. Gebruik van algemene simboliek. Wanneer daar met matrikse gewerk word, is dit algemeen om te verwys na die rye met die afkorting R en die kolomme met die afkorting C. Jy kan syfers saam met hierdie letters gebruik om `n spesifieke ry of kolom aan te dui. Byvoorbeeld, om ry 1 van `n matriks aan te dui, kan jy R1 skryf. Ry 2 word dan R2.

Jy kan enige spesifieke posisie in `n matriks aandui deur `n kombinasie van R en C te gebruik. Byvoorbeeld, om `n term in die tweede ry, derde kolom aan te dui, kan jy dit R2C3 noem.

Deel 2 van 4: Leer die bewerkings vir die oplossing van `n stelsel met `n matriks

1. Verstaan die vorm van die oplossingmatriks. Voordat jy jou stelsel van vergelykings begin oplos, moet jy verstaan wat jy met die matriks gaan doen. Op hierdie punt het jy `n matriks wat soos volg lyk:

31-19
2-21-3
1117
Jy werk met `n aantal basiese bewerkings om die `oplossingsmatriks` te skep. Die oplossingmatriks sal soos volg lyk:
100x
010j
001z
Let daarop dat die matriks bestaan uit 1`e in `n diagonale lyn met 0`e in alle ander spasies behalwe die vierde kolom. Die getalle in die vierde kolom is die oplossings vir die veranderlikes x, y en z.

2. Gebruik skalêre vermenigvuldiging. Die eerste hulpmiddel tot jou beskikking om `n stelsel met behulp van `n matriks op te los, is skalêre vermenigvuldiging. Dit is bloot `n term wat beteken dat jy die elemente in `n ry van die matriks vermenigvuldig met `n konstante getal (nie `n veranderlike nie). Wanneer jy skalêre vermenigvuldiging gebruik, hou in gedagte dat jy elke term van die hele ry moet vermenigvuldig met watter getal jy ook al kies. As jy die eerste term vergeet en net vermenigvuldig, sal jy `n verkeerde oplossing kry. Jy hoef egter nie die hele matriks op dieselfde tyd te vermenigvuldig nie. Met skalêre vermenigvuldiging werk jy net op een ry op `n slag.

Dit is algemeen om breuke in skalêre vermenigvuldiging te gebruik, want dikwels wil jy `n diagonale ry van 1`e kry. Raak gewoond daaraan om met breuke te werk. Dit sal ook makliker wees (vir die meeste stappe in die oplossing van die matriks) om jou breuke in onbehoorlike vorm te kan skryf, en dan terug te skakel na gemengde getalle vir die finale oplossing. Daarom is die getal 1 2/3 makliker om mee te werk as jy dit as 5/3 skryf.

Byvoorbeeld, die eerste ry (R1) van ons voorbeeldprobleem begin met die terme [3.1,-1,9]. Die oplossingmatriks moet `n 1 in die eerste posisie van die eerste ry bevat. Om die 3 in `n 1 te `verander`, kan ons die hele ry met 1/3 vermenigvuldig. Dit skep die nuwe R1 van [1.1/3,-1/3.3].

Maak seker dat jy enige negatiewe tekens laat waar hulle hoort.

3. Gebruik ry-optelling of ry-aftrekking. Die tweede hulpmiddel wat jy kan gebruik, is om twee rye van die matriks op te tel of af te trek. Om die 0 terme in jou oplossingmatriks te skep, moet jy getalle optel of aftrek om by die 0 uit te kom. Byvoorbeeld, as R1 van `n matriks [1,4,3,2] is en R2 is [1,3,5,8], dan kan jy die eerste ry van die tweede ry aftrek en `n nuwe ry skep [ 0,-1, 2,6], want 1-1=0 (eerste kolom), 3-4=-1 (tweede kolom), 5-3=2 (derde kolom) en 8-2=6 (vierde kolom) kolom). Wanneer jy `n ry optel of aftrek, herskryf jou nuwe resultaat in plaas van die ry waarmee jy begin het. In hierdie geval sal ons ry 2 uithaal en die nuwe ry invoeg [0,-1,2,6].

Jy kan verkorte notasie gebruik en hierdie bewerking verklaar as R2-R1=[0,-1,2,6].

Onthou dat optel en aftrekking net teenoorgestelde vorme van dieselfde bewerking is. Jy kan daaraan dink as om twee getalle by te tel of die teenoorgestelde af te trek. Byvoorbeeld, as jy met die eenvoudige vergelyking 3-3=0 begin, kan jy hieraan dink as `n optelprobleem van 3+(-3)=0. Die resultaat is dieselfde. Dit lyk eenvoudig, maar dit is soms makliker om `n probleem in een of ander vorm te oorweeg. Hou net jou negatiewe tekens dop.

4. Kombineer ryoptelling en skalêre vermenigvuldiging in `n enkele stap. Jy kan nie verwag dat die terme altyd ooreenstem nie, so kan `n eenvoudige optel of aftrekking gebruik om 0`e in jou matriks te skep. Meer dikwels sal jy `n veelvoud van `n ander ry moet optel (of aftrek). Om dit te doen, doen eers die skalêre vermenigvuldiging en voeg dan daardie resultaat by die teikenry wat jy probeer verander.

Paar; dat daar `n ry 1 van [1,1,2,6] is en `n ry 2 van [2,3,1,1]. Jy wil `n 0-term in die eerste kolom van R2 hê. Dit wil sê, jy wil die 2 na `n 0 verander. Om dit te doen moet jy `n 2 aftrek. Jy kan `n 2 kry deur eers ry 1 te vermenigvuldig met die skalêre vermenigvuldiging 2, en dan die eerste ry van die tweede ry af te trek. In verkorte vorm kan dit geskryf word as R2-2*R1. Vermenigvuldig eers R1 met 2 om [2,2,4,12] te kry. Trek dit dan van R2 af om [(2-2),(3-2),(1-4),(1-12)] te kry. Vereenvoudig dit en jou nuwe R2 word [0,1,-3,-11].

5. Kopieer rye wat onveranderd bly terwyl jy werk. Soos jy aan die matriks werk, sal jy `n enkele ry op `n slag verander, hetsy deur skalêre vermenigvuldiging, ry-optelling of ry-aftrekking, of deur `n kombinasie van stappe. Wanneer jy een ry verander, maak seker dat jy die ander rye van jou matriks in hul oorspronklike vorm kopieer.

`n Algemene fout kom voor wanneer `n gekombineerde vermenigvuldigings- en optelstap in een beweging uitgevoer word. Gestel byvoorbeeld jy moet R1 twee keer van R2 aftrek. Wanneer jy R1 met 2 vermenigvuldig om hierdie stap te doen, onthou dat R1 nie in die matriks verander nie. Jy doen net die vermenigvuldiging om R2 te verander. Kopieer eers R1 in sy oorspronklike vorm, maak dan die verandering na R2.

6. Werk eers van bo na onder. Om die stelsel op te los, werk jy in `n baie georganiseerde patroon, en "los" in wese een term van die matriks op `n slag. Die volgorde vir `n drie-veranderlike skikking sal soos volg lyk:

1. Maak `n 1 in die eerste ry, eerste kolom (R1C1).

2. Maak `n 0 in die tweede ry, eerste kolom (R2C1).

3. Maak `n 1 in die tweede ry, tweede kolom (R2C2).

4. Maak `n 0 in die derde ry, eerste kolom (R3C1).

5. Maak `n 0 in die derde ry, tweede kolom (R3C2).

6. Maak `n 1 in die derde ry, derde kolom (R3C3).

7. Werk terug van onder na bo. Op hierdie stadium, as jy die stappe reg gedoen het, is jy halfpad deur die oplossing. Jy moet die diagonale lyn van 1`e hê, met 0`e daaronder. Die getalle in die vierde kolom maak op hierdie stadium nie saak nie. Nou werk jy soos volg terug:

Skep `n 0 in die tweede ry, derde kolom (R2C3).

Skep `n 0 in die eerste ry, derde kolom (R1C3).

Skep `n 0 in die eerste ry, tweede kolom (R1C2).

8. Kyk of jy die oplossingmatriks geskep het. As jou werk korrek is, het jy die oplossingmatriks geskep met 1`e in `n diagonale lyn van R1C1, R2C2, R3C3 en 0`e in die ander posisies van die eerste drie kolomme. Die getalle in die vierde kolom is die oplossings vir jou lineêre stelsel.

Deel 3 van 4: Stel die stappe saam om die stelsel op te los

1. Begin met `n voorbeeldstelsel van lineêre vergelykings. Om hierdie stappe te oefen, kom ons begin met die stelsel wat ons vroeër gebruik het: 3x+y-z=9, 2x-2y+z=-3, en x+y+z=7. As jy dit in `n matriks skryf, het jy R1= [3.1,-1,9], R2=[2,-2,1,-3] en R3=[1,1,1,7].

2. Skep `n 1 in die eerste posisie R1C1. Let daarop dat R1 tans met `n 3 begin. Jy moet dit verander na `n 1. Jy kan dit doen deur skalêre vermenigvuldiging, deur al vier terme van R1 met 1/3 te vermenigvuldig. In snelskrif kan jy skryf as R1*1/3. Dit gee `n nuwe resultaat vir R1 as R1=[1,1/3,-1/3,3]. Neem R2 en R2, onveranderd, aan as R2=[2,-2,1,-3] en R3=[1,1,1,7].

Let daarop dat vermenigvuldiging en deling net omgekeerde funksies van mekaar is. Ons kan sê dat ons vermenigvuldig met 1/3 of deel met 3, sonder om die resultaat te verander.

3. Skep `n 0 in die tweede ry, eerste kolom (R2C1). Op hierdie punt R2=[2,-2,1,-3]. Om nader aan die oplossingmatriks te kom, moet jy die eerste term van `n 2 na `n 0 verander. Jy kan dit doen deur twee keer die waarde van R1 af te trek, aangesien R1 met `n 1 begin. In snelskrif is die operasie R2-2*R1. Onthou dat jy nie R1 verander nie, werk net daarmee. Kopieer dus eers R1 as R1=[1,1/3,-1/3,3]. As jy dan elke term van R1 verdubbel, kry jy 2*R1=[2,2/3,-2/3,6]. Ten slotte, trek hierdie resultaat van die oorspronklike R2 af om jou nuwe R2 te kry. Werk kwartaal vir kwartaal, hierdie aftrekking word (2-2), (-2-2/3), (1-(-2/3), (-3-6). Ons vereenvoudig dit na die nuwe R2=[0,-8/3,5/3,-9]. Let daarop dat die eerste term 0 is (wat ook al jou doelwit was).

Skryf ry 3 (wat nie verander het nie) as R3=[1,1,1,7].

Wees versigtig wanneer jy negatiewe getalle aftrek om seker te maak dat die karakters korrek bly.

Laat ons nou eers die breuke in hul onbehoorlike vorm plaas. Dit maak latere stappe van die oplossing makliker. Jy kan die breuke in die laaste stap van die probleem vereenvoudig.

4. Skep `n 1 in die tweede ry, tweede kolom (R2C2). Om aan te hou om die diagonale lyn van 1`e te vorm, moet jy die tweede term -8/3 in 1 omskakel. Doen dit deur die hele ry te vermenigvuldig met die wederkerige van daardie getal (-3/8). Simbolies is hierdie stap R2*(-3/8). Die gevolglike tweede ry is R2=[0.1,-5/8.27/8].

Let daarop dat, as die linker helfte van die ry begin lyk soos die oplossing met die 0 en 1, die regter helfte lelik kan lyk, met onbehoorlike breuke. Los hulle net vir wat hulle nou is.

Onthou om voort te gaan om die onaangeraakte rye te kopieer, dus R1=[1,1/3,-1/3,3] en R3=[1,1,1,7].

5. Skep `n 0 in die derde ry, eerste kolom (R3C1). Jou fokus beweeg nou na die derde ry, R3=[1,1,1,7]. Om `n 0 in die eerste posisie te maak, moet jy `n 1 aftrek van die 1 wat tans in daardie posisie is. As jy opkyk, is daar `n 1 in die eerste posisie van R1. Jy hoef dus net R1 van R3 af te trek om die resultaat te kry wat jy nodig het. Werk kwartaal vir kwartaal dit word (1-1), (1-1/3), (1-(-1/3)), (7-3). Hierdie vier mini-probleme kan dan vereenvoudig word na die nuwe R3=[0.2/3.4/3.4].

Gaan voort met kopieer langs R1=[1.1/3,-1/3.3] en R2=[0.1,-5/8.27/8]. Onthou jy verander net een ry op `n slag.

6. Maak `n 0 in die derde ry, tweede kolom (R3C2). Hierdie waarde is tans 2/3, maar moet na `n 0 omgeskakel word. Met die eerste oogopslag lyk dit of jy dubbele aftrekking van die R1-waardes kan doen, aangesien die ooreenstemmende kolom van R1 `n 1/3 bevat. As jy egter al die waardes van R1 verdubbel en aftrek, verander die 0 in die eerste kolom van R3, wat jy nie wil hê nie. Dit sal `n stap terug in jou oplossing wees. Jy moet dus met een of ander kombinasie van R2 werk. As jy 2/3 van R2 aftrek, skep jy `n 0 in die tweede kolom, sonder om die eerste kolom te verander. In verkorte vorm is dit R3- 2/3*R2. Die individuele terme word (0-0), (2/3-2/3), (4/3-(-5/3*2/3)), (4-27/8*2/3). Vereenvoudiging gee dan R3=[0,0,42/24.42/24].

7. Skep `n 1 in die derde ry, derde kolom (R3C3). Dit is `n eenvoudige vermenigvuldiging met die wederkerige van die getal wat dit sê. Die huidige waarde is 42/24, so jy kan vermenigvuldig met 24/42 om die gewenste waarde van 1 te kry. Let daarop dat die eerste twee terme albei 0 is, so enige vermenigvuldiging bly 0. Die nuwe waarde van R3=[0,0,1,1].

Let daarop dat die breuke wat in die vorige stap redelik ingewikkeld gelyk het, reeds begin oplos.

Gaan voort met R1=[1.1/3,-1/3.3] en R2=[0.1,-5/8.27/8].

Let daarop dat jy op hierdie punt die diagonaal van 1`e vir jou oplossingmatriks het. Jy hoef net drie elemente van die matriks in 0`e om te skakel om jou oplossing te vind.

8. Skep `n 0 in die tweede ry, derde kolom. R2 is tans [0.1,-5/8.27/8], met `n waarde van -5/8 in die derde kolom. Jy moet dit omskep na `n 0. Dit beteken dat jy een of ander bewerking met R3 moet uitvoer wat bestaan uit die byvoeging van 5/8. Aangesien die ooreenstemmende derde kolom van R3 `n 1 is, moet jy al die waardes van R3 met 5/8 vermenigvuldig en die resultaat by R2 tel. In kort is dit R2+5/8*R3. Kwartaal vir kwartaal is dit R2=(0+0), (1+0), (-5/8+5/8), (27/8+5/8). Dit kan vereenvoudig word na R2=[0,1,0,4].

Neem dan R1=[1,1/3,-1/3,3] en R3=[0,0,1,1].

9. Skep `n 0 in die eerste ry, derde kolom (R1C3). Die eerste ry is tans R1=[1.1/3,-1/3.3]. Jy moet die -1/3 in die derde kolom omskakel na `n 0, met `n kombinasie van R3. Jy wil nie R2 gebruik nie, want die 1 in die tweede kolom van R2 sal die R1 op die verkeerde manier verander. So jy vermenigvuldig R3*1/3 en tel die resultaat by R1. Die notasie hiervoor is R1+1/3*R3. Om dit kwartaal vir kwartaal uit te werk, lei tot R1=(1+0), (1/3+0), (-1/3+1/3), (3+1/3). Jy kan dit vereenvoudig na `n nuwe R1=[1,1/3,0,10/3].

Neem die onveranderde R2=[0,1,0,4] en R3=[0,0,1,1].

10. Maak `n 0 in die eerste ry, tweede kolom (R1C2). As alles reg gedoen word, behoort dit die laaste stap te wees. Jy moet die 1/3 in die tweede kolom omskakel na `n 0. Jy kan dit kry deur R2*1/3 te vermenigvuldig en af te trek. In kort is dit R1-1/3*R2. Die resultaat is R1=(1-0), (1/3-1/3), (0-0), (10/3-4/3). Vereenvoudiging gee dan R1=[1,0,0,2].

11. Soek die oplossingmatriks. Op hierdie stadium, as alles goed gegaan het, sou jy die drie rye R1=[1,0,0,2], R2=[0,1,0,4] en R3=[0,0,1,1] hê moet he. Let daarop dat as jy dit in blokmatriksvorm skryf met die rye bo-op mekaar, het jy diagonale 1`e met 0`e verder aan, en jou oplossings is in die vierde kolom. Die oplossingmatriks moet soos volg lyk:

1002

0104

0011

12. Verstaan jou oplossing. Sodra jy die lineêre vergelykings na `n matriks omgeskakel het, plaas die x-koëffisiënte in die eerste kolom, die y-koëffisiënte in die tweede kolom, die z-koëffisiënte in die derde kolom. As jy nou die matriks na vergelykings wil herskryf, beteken hierdie drie lyne van die matriks eintlik die drie vergelykings 1x+0y+0z=2, 0x+1y+0z=4, en 0x+0y+1z=1. Aangesien ons die 0 terme kan deurtrek en nie die 1-koëffisiënte hoef te skryf nie, vereenvoudig hierdie drie vergelykings tot die oplossing, x=2, y=4 en z=1. Dit is die oplossing vir jou stelsel lineêre vergelykings.

Deel 4 van 4: Kontroleer jou oplossing

1. Verwerk die oplossings in elke veranderlike in elke vergelyking. Dit is altyd `n goeie idee om te kyk of jou oplossing werklik korrek is. Jy doen dit deur jou resultate in die oorspronklike vergelykings te toets.

Die oorspronklike vergelykings vir hierdie probleem was: 3x+y-z=9, 2x-2y+z=-3, en x+y+z=7. Wanneer jy die veranderlikes vervang met hul waardes wat jy gevind het, kry jy 3*2+4-1=9, 2*2-2*4+1=-3, en 2+4+1=7.

2. Vereenvoudig enige vergelyking. Voer die bewerkings in elke vergelyking uit volgens die basiese reëls van bewerkings. Die eerste vergelyking vereenvoudig na 6+4-1=9, of 9=9. Die tweede vergelyking kan vereenvoudig word na 4-8+1=-3, of -3=-3. Die laaste vergelyking is eenvoudig 7=7.

Aangesien elke vergelyking tot `n ware wiskundige stelling vereenvoudig, is jou oplossings korrek. Indien enige van die oplossings nie korrek is nie, gaan asseblief weer jou werk na en kyk vir enige foute. Sommige algemene foute kom voor wanneer jy ontslae raak van minustekens langs die pad of wanneer die vermenigvuldiging en optel van breuke verwar word.

3. Skryf jou finale oplossings neer. Vir hierdie gegewe probleem is die finale oplossing x=2, y=4 en z=1.

Wenke

As jou stelsel vergelykings baie kompleks is, met baie veranderlikes, wil jy dalk `n grafiese sakrekenaar gebruik in plaas daarvan om die werk met die hand te doen. Vir inligting hieroor kan jy ook wikiHow raadpleeg.