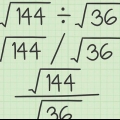Deel matrikse (met prente)

Inhoud

Trappe
Wenke
Waarskuwings

As jy weet hoe om twee matrikse met mekaar te vermenigvuldig, dan is jy goed op pad om een matriks deur `n ander matriks te kan `deel`. Deling is tussen aanhalingstekens omdat matrikse tegnies nie verdeel kan word nie. In plaas daarvan vermenigvuldig ons die een matriks met die omgekeerde uit `n ander matriks. Hierdie berekeninge word dikwels gebruik om stelsels lineêre vergelykings op te los.

Trappe

Deel 1 van 3: Verstaan dat `deel` onmoontlik is

1. Verstaan wat `deel` van `n matriks beteken. Tegnies bestaan daar nie iets soos matriksverdeling nie. Die verdeling van matrikse is nie `n gedefinieerde funksie nie. Die naaste daaraan is vermenigvuldiging met die inverse van `n ander matriks. Met ander woorde, alhoewel [A] ÷ [B] nie gedefinieer is nie, kan jy die probleem oplos [A] * [B]. Aangesien hierdie twee vergelykings gelykstaande is aan skalare, "voel" dit soos `n matriksverdeling, maar dit is belangrik om die korrekte terminologie te gebruik.

Let daarop dat [A] * [B] en [B] * [A] nie dieselfde probleem is nie. Jy sal dalk albei moet oplos om alle moontlike antwoorde te vind.
Byvoorbeeld, in plaas van $(\begin{matrix} 13 & 26 \\ 39 & 13 \end{matrix}) \div (\begin{matrix} 7 & 4 \\ 2 & 3 \end{matrix})$ ${begin{pmatrix}13&26\39&13end{pmatrix}}div {begin{pmatrix}7&4\2&3end{pmatrix}}$ , skryf $(\begin{matrix} 13 & 26 \\ 39 & 13 \end{matrix}) *^{(\begin{matrix} 7 & 4 \\ 2 & 3 \end{matrix}) - 1}$ ${begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}^{{-1}}$ .
miskien moet jy ook $(\begin{matrix} 7 & 4 \\ 2 & 3 \end{matrix}) - 1 * (\begin{matrix} 13 & 26 \\ 39 & 13 \end{matrix})$ ${begin{pmatrix}7&4\2&3end{pmatrix}}^{{-1}}*{begin{pmatrix}13&26\39&13end{pmatrix}}$ bereken, wat dalk net `n ander antwoord kan oplewer.

2. Kontroleer die `deler-matriks` vierkant is. Om die inverse van `n matriks te kan bepaal, moet dit `n vierkantige matriks wees, dus met dieselfde aantal rye en kolomme. As die matriks waarvan jy die inverse wil vind nie `n vierkantige matriks is nie, dan is daar geen unieke oplossing vir die probleem nie.

Die term `delermatriks` is `n bietjie los, want dit gaan nie eintlik oor `n delingsprobleem nie. Vir [A] * [B] verwys dit na matriks [B]. In ons voorbeeld is dit

(\begin{matrix} 7 & 4 \\ 2 & 3 \end{matrix})

${begin{pmatrix}7&4\2&3end{pmatrix}}$ .

`n Matriks met `n inverse word `omkeerbaar` of `nie-enkelvoud` genoem.` Matrikse sonder inverse is `enkelvoud.`

3. Kyk of die twee matrikse met mekaar vermenigvuldig kan word. Om twee matrikse saam te vermenigvuldig, moet die aantal kolomme in die eerste matriks gelyk wees aan die aantal rye in die tweede matriks. As dit nie in beide gevalle werk nie ([A] * [B] of [B] * [A]), is daar geen oplossing vir die probleem nie.

Byvoorbeeld, as [A] `n 4 x 3-matriks (4 rye, 3 kolomme) is en [B] `n 2 x 2-matriks (2 rye, 2 kolomme) is, dan is daar geen oplossing nie. [A] * [B] werk nie omdat 3 ≠ 2, en [B] * [A] werk nie omdat 2 ≠ 4.

Weet dat die inverse [B] altyd dieselfde aantal rye en kolomme het as die oorspronklike matriks [B]. Dit is nie nodig om die inverse te bereken om hierdie stap te voltooi nie.

In ons voorbeeldprobleem is beide matrikse 2 x 2, dus kan hulle in enige volgorde vermenigvuldig word.

4. Bepaal die determinant van `n 2 x 2 matriks. Daar is nog een vereiste kontrole voordat jy die inverse van `n matriks kan bepaal. Die determinant van die matriks kan nie nul wees nie. As die determinant nul is, dan het die matriks geen inverse nie. Hier is hoe om die determinant te bepaal in die eenvoudigste geval (die 2 x 2 matriks):

2×2 matriks: die determinant van die matriks

(\begin{matrix} a & b \\ c & d \end{matrix})

${begin{pmatrix}a&b\c&dend{pmatrix}}$ is ad - bc. Met ander woorde, neem die produk van die hoofhoeklyn (links bo na regs onder), trek dan die produk van die antidiagonaal (regs bo na links onder) van daar af.

Byvoorbeeld, die matriks

(\begin{matrix} 7 & 4 \\ 2 & 3 \end{matrix})

${begin{pmatrix}7&4\2&3end{pmatrix}}$ het die determinant (7)(3) - (4)(2) = 21 - 8 = 13. Dit is nie nul nie, dus is dit moontlik om die inverse te bepaal.

5. Bepaal die determinant van `n groter matriks. As jou matriks 3 x 3 of groter is, is nog werk nodig om die determinant te bepaal:

3 x 3 matriks: Kies `n element en kruis die ry en kolom waaraan dit behoort. Bepaal die determinant van die oorblywende 2 x 2 matriks, vermenigvuldig met die gekose element, en hou `n matrikstekentabel om die teken te bepaal. Herhaal vir die ander twee elemente in dieselfde ry en kolom as die eerste wat jy gekies het, en tel dan al drie determinante bymekaar. Lees hierdie artikel vir stap-vir-stap instruksies en wenke om dit vinniger te doen.

Groter matrikse: Gebruik van `n grafiese sakrekenaar of sagteware word hier aanbeveel. Die metode is soortgelyk aan dié van `n 3 x 3 matriks, maar neem baie tyd as jy dit met die hand doen. Byvoorbeeld, om die determinant van `n 4 x 4 matriks te vind, moet jy eers die determinante van vier 3 x 3 matrikse vind.

6. Aanhou. As jou matriks nie `n vierkant is nie, of as die determinant daarvan nul is, skryf dit as `geen unieke oplossing`. Die probleem is opgelos. As die matriks `n vierkant is en die determinant daarvan nie nul is nie, gaan na die volgende deel vir die volgende stap: vind die inverse.

Deel 2 van 3: Omkering van die matriks

1. Ruil die posisies van die elemente van die 2 x 2 hoofhoeklyn om. As jy met `n 2 x 2 matriks te doen het, kan jy `n kortpad gebruik om hierdie berekening baie makliker te maak. Die eerste stap van hierdie vinnige oplossing behels die omruiling van die boonste-linker element met die onder-regs element. Byvoorbeeld:

$(\begin{matrix} 7 & 4 \\ 2 & 3 \end{matrix})$ ${begin{pmatrix}7&4\2&3end{pmatrix}}$ → $(\begin{matrix} 3 & 4 \\ 2 & 7 \end{matrix})$ ${begin{pmatrix}3&4\2&7end{pmatrix}}$
Opmerking: Die meeste mense gebruik `n sakrekenaar om die inverse van `n 3 x 3 matriks (of groter) te bepaal. As jy dit nog met die hand wil bereken, kyk aan die einde van hierdie deel.

2. Neem die teenoorgestelde van die ander twee elemente, maar laat hulle in daardie posisie. Met ander woorde, vermenigvuldig die top oordeel en onderkant links-elemente met-1:

(\begin{matrix} 3 & 4 \\ 2 & 7 \end{matrix})

${begin{pmatrix}3&4\2&7end{pmatrix}}$ →

(\begin{matrix} 3 & - 4 \\ - 2 & 7 \end{matrix})

${begin{pmatrix}3&-4\-2&7end{pmatrix}}$

3. Neem die wederkerige van die determinant. Jy het die determinant van hierdie matriks in die afdeling hierbo gevind, so dit is nie nodig om dit weer te bereken nie. Skryf net die wederkerige van 1/(determinant):

In ons voorbeeld is die determinant 13. Die wederkerige hiervan is

\frac{1}{13}

${frac{1}{13}}$ .

4. Vermenigvuldig die nuwe matriks met die resiproke van die determinant. Vermenigvuldig elke element van die nuwe matriks met die wederkerige wat jy sopas gevind het. Die resulterende matriks is die inverse van die 2 x 2 matriks:

\frac{1}{13} * (\begin{matrix} 3 & - 4 \\ - 2 & 7 \end{matrix})

${frac{1}{13}}*{begin{pmatrix}3&-4\-2&7end{pmatrix}}$
=

(\begin{matrix}  \end{matrix} \frac{3}{13} - 4 13 - 2 13 & \frac{7}{13})

${begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}$

5. Bevestig dat die inverse korrek is. Om jou werk na te gaan, vermenigvuldig die inverse met die oorspronklike matriks. As die inverse korrek is, dan is hul produk altyd die identiteit van die matriks,

(\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix})

${begin{pmatrix}1&0\0&1end{pmatrix}}$ As dit wiskundig korrek is, gaan voort na die volgende afdeling om die probleemuitwerking te voltooi.

Vir die doel van die voorbeeldprobleem vermenigvuldig ons

(\begin{matrix}  \end{matrix} \frac{3}{13} - 4 13 - 2 13 & \frac{7}{13}) * (\begin{matrix} 7 & 4 \\ 2 & 3 \end{matrix}) = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix})

${begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}={begin{pmatrix}1&0\0&1end{pmatrix} }}$ .

Sien wikihow vir meer inligting oor die vermenigvuldiging van matrikse.

Let wel: Matriksvermenigvuldiging is nie kommutatief nie: die volgorde van die faktore maak saak. Wanneer `n matriks met sy inverse vermenigvuldig word, sal beide die identiteitsmatriks tot gevolg hê.

6.Bepaal die matriksinversie van `n 3 x 3 matriks of groter. Tensy jy nuut in hierdie proses is, kan jy jouself baie tyd bespaar deur `n grafiese sakrekenaar of wiskunde sagteware op groter matrikse te gebruik. As jy dit met die hand moet bereken, hier is `n vinnige opsomming van een metode wat jy kan gebruik:

Voeg die identiteitsmatriks I aan die regterkant van jou matriks by. Byvoorbeeld, [B] → [B | ek]. Die identiteitsmatriks het `1`-elemente langs die hoofdiagonaal, en `0`-elemente in alle ander posisies.

Doen rybewerkings om die matriks te verklein totdat die linkerkant in ry-vlakvorm is, gaan dan voort om te verminder totdat die linkerkant die identiteitsmatriks is.

Wanneer die hele bewerking voltooi is, is jou matriks in die vorm [I | B]. Met ander woorde, die regterkant word die inverse van die oorspronklike matriks.

Deel 3 van 3: Vermenigvuldig die matrikse om die probleem te voltooi

1. Skryf beide moontlike vergelykings neer. In "gewone wiskunde" met skalare is vermenigvuldiging kommutatief; 2 x 6 = 6 x 2. Dit is nie van toepassing op matrikse nie, so jy sal dalk twee probleme moet oplos:

[A] * [B] is die oplossing X vir probleem X[B] = [A].
[B] * [A] is die oplossing X vir probleem [B]X = [A].
As dit deel van `n vergelyking is, maak seker dat jy dieselfde bewerking aan beide kante van die vergelyking toepas. As [A] = [C], dan is [B][A] nie gelyk aan [C][B], want [B] is links van [A], maar regs van [C].

2. Bepaal die afmetings van jou antwoord. Die afmetings van die finale matriks is die buitenste afmetings van die twee faktore. Dit het dieselfde aantal rye as die eerste matriks, en dieselfde aantal kolomme as die tweede matriks.

Om terug te keer na die oorspronklike voorbeeld: beide

(\begin{matrix} 13 & 26 \\ 39 & 13 \end{matrix})

${begin{pmatrix}13&26\39&13end{pmatrix}}$ en

(\begin{matrix}  \end{matrix} \frac{3}{13} - 4 13 - 2 13 & \frac{7}{13})

${begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}$ is 2 x 2 matrikse, dus is die afmetings van die antwoord ook 2 x 2.

Om `n effens meer ingewikkelde voorbeeld te neem: as [A] `n is 4 x is `n 3-matriks en [B] is `n 3 x 3 matriks, dan het die matriks [A] * [B] afmetings 4 x 3.

3. Bepaal die waarde van die eerste element. Kyk na die gekoppelde artikel vir gedetailleerde instruksies, of verfris jou kennis met hierdie opsomming:

Om ry 1, kolom 1 van [A][B] te vind, vind die puntproduk van [A] ry 1 en [B] kolom 1. Dus, vir `n 2 x 2 matriks, bereken jy

a 1, 1 * b_{1, 1} + a_{1, 2} * b_{2, 1}

$a_{{1,1}}*b_{{1,1}}+a_{{1,2}}*b_{{2,1}}$ .

In ons voorbeeld

(\begin{matrix} 13 & 26 \\ 39 & 13 \end{matrix}) * (\begin{matrix}  \end{matrix} \frac{3}{13} - 4 13 - 2 13 & \frac{7}{13})

${begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}} \{frac{-2}{13}}&{frac{7}{13}}end{pmatrix}}$ , is ry 1 kolom 1 van jou antwoord:

(13 * \frac{3}{13}) + (26 * - 2 13)

$(13*{frac{3}{13}})+(26*{frac{-2}{13}})$

= 3 + - 4

$=3+-4$

= - 1

$=-1$

4. Bereken die puntproduk vir elke posisie in jou matriks. Byvoorbeeld, die element by posisie 2.1 is die puntproduk van [A] ry 2 en [B] kolom 1. Probeer om self die voorbeeld uit te werk. Jy behoort die volgende antwoorde te kry:

(\begin{matrix} 13 & 26 \\ 39 & 13 \end{matrix}) * (\begin{matrix}  \end{matrix} \frac{3}{13} - 4 13 - 2 13 & \frac{7}{13}) = (\begin{matrix} - 1 & 10 \\ 7 & - 5 \end{matrix})

${begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}} \{frac{-2}{13}}&{frac{7}{13}}end{pmatrix}}={begin{pmatrix}-1&10\7&-5end {pmatrix}}$

En die ander oplossing:

(\begin{matrix}  \end{matrix} \frac{3}{13} - 4 13 - 2 13 & \frac{7}{13}) * (\begin{matrix} 13 & 26 \\ 39 & 13 \end{matrix}) = (\begin{matrix} - 9 & 2 \\ 19 & 3 \end{matrix})

${begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}*{begin{pmatrix}13&26\39&13end{pmatrix}}={begin{pmatrix}-9&2\19&3end{ pmmatrix}}$

Wenke

Jy kan `n matriks deur `n skalaar deel deur elke element van die matriks deur die skalaar te deel.

Byvoorbeeld, die matriks $(\begin{matrix} 6 & 8 \\ 2 & 4 \end{matrix})$ ${begin{pmatrix}6&8\2&4end{pmatrix}}$ gedeel deur 2 = $(\begin{matrix} 3 & 4 \\ 1 & 2 \end{matrix})$ ${begin{pmatrix}3&4\1&2end{pmatrix}}$

Waarskuwings

Sakrekenaars is nie altyd 100% akkuraat in matrikswiskunde nie. Byvoorbeeld, as jou sakrekenaar aandui dat `n element `n baie klein waarde het (bv. 2E), dan is die waarde waarskynlik nul.