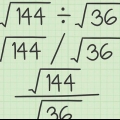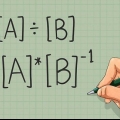Voorbeeld 1: Los op:  .
.
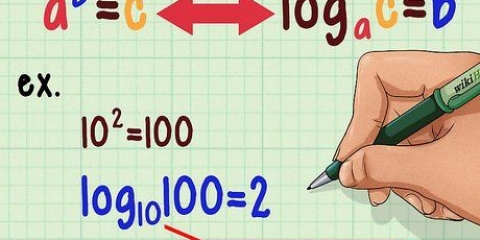
Begin deur dit na `n logaritme om te skakel deur die formule hierbo te gebruik: .
. Hierdie formule is die `verandering van basis`-formule, afgelei van die basiese logaritmiese eienskappe. 
Voorbeeld 1 (vervolg.): Herskryf  as
as  . Die waarde van `?` is die antwoord op die probleem. Jy sal dalk `n paar moet probeer om dit te vind:
. Die waarde van `?` is die antwoord op die probleem. Jy sal dalk `n paar moet probeer om dit te vind:



16 is waarna jy gesoek het, so = 4.
= 4. 
Voorbeeld 2: Wat is  ?
? Skakel dit om na `n logaritme::  .(Let daarop dat die 3 verdwyn in enige aanvanklike logboek -- dit is van toepassing op enige basis).
.(Let daarop dat die 3 verdwyn in enige aanvanklike logboek -- dit is van toepassing op enige basis). Herskryf as  en toets moontlike waardes van ?:
en toets moontlike waardes van ?:


Aangesien 58 tussen hierdie twee getalle val, het geen heelgetal as antwoord nie.
geen heelgetal as antwoord nie. Laat jou antwoord as:  .
. 

As óf x of y negatief is, is daar geen oplossing vir die probleem nie. as albei x as y negatief is, verwyder die negatiewe tekens deur die eienskap te gebruik 
Daar is geen logaritmes van negatiewe getalle in die voorbeeldprobleem nie, so jy kan voortgaan na die volgende stap. 
Gebruik dit om die linkerkant van die voorbeeldprobleem uit te brei:

Vervang dit terug in die oorspronklike vergelyking:

→


Die voorbeeldprobleem het `n nuwe term:  . Aangesien 3 = 27, vereenvoudig
. Aangesien 3 = 27, vereenvoudig  vieslik 3.
vieslik 3. Die volledige vergelyking is nou:




 .
.
In die voorbeeldprobleem, die n steeds vasgevang in die term  .
.
Rondom die n om te isoleer, gebruik die produkreël van logaritmes:

Vervang dit terug in die volledige vergelyking:





Sedert 3 = 19683, n =19683
Deel logaritmes
Inhoud
Logaritmes lyk dalk moeilik om te gebruik, maar net soos eksponente of polinome moet jy net die regte tegnieke aanleer. Jy hoef net `n paar basiese eienskappe te ken om twee logaritmes met dieselfde basis te deel, of om `n logaritme met `n kwosiënt uit te brei.
Trappe
Metode 1 van 2: Verdeel logaritmes met die hand

1. Kyk vir negatiewe getalle en ene. Hierdie metode hanteer probleme in die vorm  . Dit werk egter nie vir `n paar spesiale gevalle nie:
. Dit werk egter nie vir `n paar spesiale gevalle nie:
 . Dit werk egter nie vir `n paar spesiale gevalle nie:
. Dit werk egter nie vir `n paar spesiale gevalle nie: - Die logaritme van `n negatiewe getal word nie vir alle basisse (soos
of
). Skryf dan `Geen oplossing`.
- Die logaritme van nul is ook ongedefinieerd vir alle basisse. As jy `n term sien soos
, skryf dan ook `Geen oplossing`.
- Die logaritme van een in enige basis (
) is altyd gelyk aan nul, aangesien
vir alle waardes van X. Vervang daardie logaritme met 1 in plaas daarvan om die metode hieronder te gebruik.
- As die twee logaritmes verskillende basisse het, soos
, en jy kan nie een van hulle tot `n heelgetal vereenvoudig nie, dan kan die probleem nie met die hand opgelos word nie.

2. Wysig die uitdrukking in een logaritme. Gestel jy het nie enige van die bogenoemde uitsonderings gevind nie, kan jy nou die probleem in een logaritme vereenvoudig. Om dit te doen, gebruik die formule .
.
 .
. .
.Begin deur dit na `n logaritme om te skakel deur die formule hierbo te gebruik:
 .
.
3. Bereken dit met die hand indien moontlik. Onthou: om  om op te los, dink jy aan `
om op te los, dink jy aan ` ` of `Watter eksponent kan ek gebruik a verhef tot X om te kry?` Dit is nie altyd moontlik om dit sonder `n sakrekenaar op te los nie, maar as jy gelukkig is, sal jy met `n maklik vereenvoudigde logaritme eindig.
` of `Watter eksponent kan ek gebruik a verhef tot X om te kry?` Dit is nie altyd moontlik om dit sonder `n sakrekenaar op te los nie, maar as jy gelukkig is, sal jy met `n maklik vereenvoudigde logaritme eindig.
 om op te los, dink jy aan `
om op te los, dink jy aan ` ` of `Watter eksponent kan ek gebruik a verhef tot X om te kry?` Dit is nie altyd moontlik om dit sonder `n sakrekenaar op te los nie, maar as jy gelukkig is, sal jy met `n maklik vereenvoudigde logaritme eindig.
` of `Watter eksponent kan ek gebruik a verhef tot X om te kry?` Dit is nie altyd moontlik om dit sonder `n sakrekenaar op te los nie, maar as jy gelukkig is, sal jy met `n maklik vereenvoudigde logaritme eindig. as
as  . Die waarde van `?` is die antwoord op die probleem. Jy sal dalk `n paar moet probeer om dit te vind:
. Die waarde van `?` is die antwoord op die probleem. Jy sal dalk `n paar moet probeer om dit te vind:


16 is waarna jy gesoek het, so
 = 4.
= 4.
4. Laat die antwoord in logaritmevorm as jy dit nie kan vereenvoudig nie. Sommige logaritmes is baie moeilik om met die hand op te los. Jy benodig `n sakrekenaar as jy die antwoord vir `n praktiese doel nodig het. Wanneer jy probleme in wiskundeklas oplos, verwag jou onderwyser waarskynlik dat jy die antwoord as logaritme moet los. Hier is nog `n voorbeeld wat hierdie metode gebruik vir `n moeiliker probleem:
 ?
? .(Let daarop dat die 3 verdwyn in enige aanvanklike logboek -- dit is van toepassing op enige basis).
.(Let daarop dat die 3 verdwyn in enige aanvanklike logboek -- dit is van toepassing op enige basis). en toets moontlike waardes van ?:
en toets moontlike waardes van ?:

Aangesien 58 tussen hierdie twee getalle val, het
 geen heelgetal as antwoord nie.
geen heelgetal as antwoord nie. .
.Metode 2 van 2: Werk met die logaritme van `n kwosiënt

1. Begin met `n deelprobleem in `n logaritme. Hierdie afdeling help jou om probleme met uitdrukkings in die vorm op te los  .
.
 .
. - Begin byvoorbeeld met hierdie probleem:
`Los op vir n if.`

2. Kyk vir negatiewe getalle. Die logaritme van `n negatiewe getal is ongedefinieerd. As x of y `n negatiewe getal is, kyk of die probleem `n oplossing het voordat jy voortgaan:


3. Verdeel die kwosiënt in twee logaritmes. `n Nuttige eienskap van logaritmes word beskryf deur die formule:  . Met ander woorde, die logaritme van `n kwosiënt is altyd gelyk aan die logaritme van die teller, minus die logaritme van die noemer.
. Met ander woorde, die logaritme van `n kwosiënt is altyd gelyk aan die logaritme van die teller, minus die logaritme van die noemer.
 . Met ander woorde, die logaritme van `n kwosiënt is altyd gelyk aan die logaritme van die teller, minus die logaritme van die noemer.
. Met ander woorde, die logaritme van `n kwosiënt is altyd gelyk aan die logaritme van die teller, minus die logaritme van die noemer.

→


4. Vereenvoudig die logaritmes indien moontlik. As enige van die nuwe logaritmes in die uitdrukking `n heelgetal is, vereenvoudig dit nou.
 . Aangesien 3 = 27, vereenvoudig
. Aangesien 3 = 27, vereenvoudig  vieslik 3.
vieslik 3.

5. Isoleer die veranderlike. Soos enige wiskundeprobleem, help dit om die term met die veranderlike aan die een kant van die vergelyking te isoleer. Elimineer soortgelyke terme waar moontlik om die vergelyking te vereenvoudig.


 .
.
6. Gebruik bykomende eienskappe van logaritmes wanneer nodig. Om die veranderlike van ander terme binne dieselfde logaritme te isoleer, herskryf die term deur verskillende logaritmiese eienskappe te gebruik.
 .
.Rondom die n om te isoleer, gebruik die produkreël van logaritmes:





7. Gaan voort om te vereenvoudig totdat jy die oplossing vind. Herhaal dieselfde algebraïese en logaritmiese tegnieke om die probleem op te los. As daar geen heelgetaloplossing is nie, gebruik `n sakrekenaar en rond af tot die naaste beduidende getal.


Sedert 3 = 19683, n =19683
Artikels oor die onderwerp "Deel logaritmes"
Оцените, пожалуйста статью
Soortgelyk
Gewilde