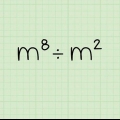Tien tot die mag van drie











Soos hier getoon, kan jy voortgaan om die basis te vermenigvuldig met die produk van elk van die eerste pare getalle totdat jy die finale antwoord kry. Hou net aan om die eerste twee getalle te vermenigvuldig, vermenigvuldig dan hierdie antwoord met die volgende getal in die ry. Dit geld vir enige eksponent. Wanneer jy klaar is met die voorbeeld, kry jy  .
. 




Gebruik `n soekenjin soos Startpage, Duckduckgo of Google om die antwoord te vind. Jy kan die `^`-knoppie op jou rekenaar, tablet of slimfoon gebruik om die uitdrukking in die soekkassie in te voer, en jy sal dadelik die antwoord sien, en voorstelle vir soortgelyke uitdrukkings om te verken (Duckduckgo wys selfs `n volledige sakrekenaar). 





Aangesien alles dieselfde getal is, maar vermenigvuldig, kan ons hierdie kombineer: 




Aangesien die basisse dieselfde is, kan jy hulle net bymekaar voeg: 




Soos jy binne `n oomblik sal sien, is enige getal wat deel is van `n breuk, soos  , herskryf word as
, herskryf word as  . Negatiewe eksponente vorm breuke.
. Negatiewe eksponente vorm breuke. 
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Onthou dat `n getal sonder `n mag `n eksponent van 1 het
Onthou dat `n getal sonder `n mag `n eksponent van 1 het =
= 
 =
= 




![Oplossing van eksponente x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Oplossing van eksponente ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)



Oplossing van eksponente
Inhoud
Eksponente word gebruik wanneer `n getal met homself vermenigvuldig word. In plaas van 



Trappe
Metode 1 van 3: Los eenvoudige eksponente op

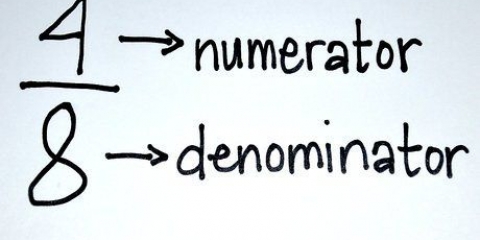
1. Leer die korrekte terme en woordeskat vir eksponensiële probleme. Het jy `n eksponent soos  , dan werk jy met twee eenvoudige dele. Die onderstelnommer hier is `n 2, of die basis. Hierdie getal word verhoog tot die krag van 3, ook bekend as die eksponent of krag. Praat ons van
, dan werk jy met twee eenvoudige dele. Die onderstelnommer hier is `n 2, of die basis. Hierdie getal word verhoog tot die krag van 3, ook bekend as die eksponent of krag. Praat ons van  , dan sê ons `twee tot die derde mag`, `twee tot die derde mag`, of `twee verhoog tot die derde mag`.`
, dan sê ons `twee tot die derde mag`, `twee tot die derde mag`, of `twee verhoog tot die derde mag`.`
 , dan werk jy met twee eenvoudige dele. Die onderstelnommer hier is `n 2, of die basis. Hierdie getal word verhoog tot die krag van 3, ook bekend as die eksponent of krag. Praat ons van
, dan werk jy met twee eenvoudige dele. Die onderstelnommer hier is `n 2, of die basis. Hierdie getal word verhoog tot die krag van 3, ook bekend as die eksponent of krag. Praat ons van  , dan sê ons `twee tot die derde mag`, `twee tot die derde mag`, of `twee verhoog tot die derde mag`.`
, dan sê ons `twee tot die derde mag`, `twee tot die derde mag`, of `twee verhoog tot die derde mag`.` - As `n getal tot die tweede mag verhoog word, soos
, dan kan jy ook sê dat die getal is vierkantig is, soos `vyf kwadraat.`
- As `n getal tot die derde mag verhoog word, soos
, dan kan jy ook daardie nommer a sê kubusnommer is.
- As `n getal sonder `n eksponent genoem word, soos byvoorbeeld 4, dan is dit teoreties in die eerste mag en kan herskryf word as
.
- As die eksponent gelyk is aan 0, en `n `getal (nie-nul)` word verhoog tot die `nul mag`, dan is die heelgetal gelyk aan 1, as
of selfs iets soos
Meer hieroor in die `Wenke`-afdeling.

2. Vermenigvuldig die basis die aantal kere op sigself soos aangedui deur die eksponent. As jy `n krag met die hand moet oplos, begin jy deur dit as `n vermenigvuldiging te herskryf. Jy vermenigvuldig die basis die aantal kere met homself, soos aangedui deur die eksponent. So, het jy  dan vermenigvuldig jy drie vier keer met homself
dan vermenigvuldig jy drie vier keer met homself  . Nog `n paar voorbeelde is:
. Nog `n paar voorbeelde is:
 dan vermenigvuldig jy drie vier keer met homself
dan vermenigvuldig jy drie vier keer met homself  . Nog `n paar voorbeelde is:
. Nog `n paar voorbeelde is:



3. Los `n uitdrukking op: Vermenigvuldig die eerste twee getalle saam om die produk te kry. Byvoorbeeld, met  , begin jy met
, begin jy met  Dit lyk na `n vervelige taak, maar doen dit net stap vir stap. Begin deur die eerste twee viere te vermenigvuldig. Vervang dan die twee viere met die antwoord soos hieronder getoon:
Dit lyk na `n vervelige taak, maar doen dit net stap vir stap. Begin deur die eerste twee viere te vermenigvuldig. Vervang dan die twee viere met die antwoord soos hieronder getoon:
 , begin jy met
, begin jy met  Dit lyk na `n vervelige taak, maar doen dit net stap vir stap. Begin deur die eerste twee viere te vermenigvuldig. Vervang dan die twee viere met die antwoord soos hieronder getoon:
Dit lyk na `n vervelige taak, maar doen dit net stap vir stap. Begin deur die eerste twee viere te vermenigvuldig. Vervang dan die twee viere met die antwoord soos hieronder getoon:



4. Vermenigvuldig die antwoord van die eerste paar (16) met die volgende getal. Hou aan om die getalle te vermenigvuldig om jou eksponent te `groei`. Om voort te gaan met ons voorbeeld, vermenigvuldig ons 16 met die volgende 4 sodat:






 .
.
5. Probeer ook die volgende voorbeelde en kontroleer jou antwoorde met `n sakrekenaar.




6. Gebruik die `exp,` `X n  ` of `^` knoppie van jou sakrekenaar vir die eksponente. Dit is byna onmoontlik om groter eksponente te vind, soos
` of `^` knoppie van jou sakrekenaar vir die eksponente. Dit is byna onmoontlik om groter eksponente te vind, soos  met die hand, maar sakrekenaars kan dit maklik hanteer. Die knoppie hiervoor word gewoonlik duidelik genoeg aangedui. Die Windows-sakrekenaar kan uitgebrei word na `n wetenskaplike sakrekenaar deur op die sakrekenaar se `View`-oortjie te klik en `Scientific` te kies. As jy die standaard sakrekenaar terug wil hê, klik weer op `View` en kies `Default`.
met die hand, maar sakrekenaars kan dit maklik hanteer. Die knoppie hiervoor word gewoonlik duidelik genoeg aangedui. Die Windows-sakrekenaar kan uitgebrei word na `n wetenskaplike sakrekenaar deur op die sakrekenaar se `View`-oortjie te klik en `Scientific` te kies. As jy die standaard sakrekenaar terug wil hê, klik weer op `View` en kies `Default`.
 ` of `^` knoppie van jou sakrekenaar vir die eksponente. Dit is byna onmoontlik om groter eksponente te vind, soos
` of `^` knoppie van jou sakrekenaar vir die eksponente. Dit is byna onmoontlik om groter eksponente te vind, soos  met die hand, maar sakrekenaars kan dit maklik hanteer. Die knoppie hiervoor word gewoonlik duidelik genoeg aangedui. Die Windows-sakrekenaar kan uitgebrei word na `n wetenskaplike sakrekenaar deur op die sakrekenaar se `View`-oortjie te klik en `Scientific` te kies. As jy die standaard sakrekenaar terug wil hê, klik weer op `View` en kies `Default`.
met die hand, maar sakrekenaars kan dit maklik hanteer. Die knoppie hiervoor word gewoonlik duidelik genoeg aangedui. Die Windows-sakrekenaar kan uitgebrei word na `n wetenskaplike sakrekenaar deur op die sakrekenaar se `View`-oortjie te klik en `Scientific` te kies. As jy die standaard sakrekenaar terug wil hê, klik weer op `View` en kies `Default`.Metode 2 van 3: Optel, aftrek en vermenigvuldig eksponente

1. Jy kan slegs maggetalle van mekaar optel of aftrek as hulle dieselfde basis en dieselfde eksponent het. As jy te doen het met identiese basisse en eksponente, soos  , dan kan jy die optelling van die terme tot `n vermenigvuldiging vereenvoudig. Moenie dit vergeet nie
, dan kan jy die optelling van die terme tot `n vermenigvuldiging vereenvoudig. Moenie dit vergeet nie  beskou kan word as
beskou kan word as  , sodat
, sodat  deur by te voeg, waar `1 van daardie + 1 van daardie = 2 van daardie`, wat ook al `dit` mag wees. Tel net die aantal soortgelyke terme bymekaar (dié met die identiese basis en eksponent), en vermenigvuldig die som met daardie eksponensiële uitdrukking. Jy kan dan
deur by te voeg, waar `1 van daardie + 1 van daardie = 2 van daardie`, wat ook al `dit` mag wees. Tel net die aantal soortgelyke terme bymekaar (dié met die identiese basis en eksponent), en vermenigvuldig die som met daardie eksponensiële uitdrukking. Jy kan dan  los en vermenigvuldig daardie antwoord met twee. Onthou dat dit moontlik is omdat `n vermenigvuldiging niks meer is as om `n optelling te herskryf nie, want
los en vermenigvuldig daardie antwoord met twee. Onthou dat dit moontlik is omdat `n vermenigvuldiging niks meer is as om `n optelling te herskryf nie, want  . Hier is `n paar voorbeelde:
. Hier is `n paar voorbeelde:
 , dan kan jy die optelling van die terme tot `n vermenigvuldiging vereenvoudig. Moenie dit vergeet nie
, dan kan jy die optelling van die terme tot `n vermenigvuldiging vereenvoudig. Moenie dit vergeet nie  beskou kan word as
beskou kan word as  , sodat
, sodat  deur by te voeg, waar `1 van daardie + 1 van daardie = 2 van daardie`, wat ook al `dit` mag wees. Tel net die aantal soortgelyke terme bymekaar (dié met die identiese basis en eksponent), en vermenigvuldig die som met daardie eksponensiële uitdrukking. Jy kan dan
deur by te voeg, waar `1 van daardie + 1 van daardie = 2 van daardie`, wat ook al `dit` mag wees. Tel net die aantal soortgelyke terme bymekaar (dié met die identiese basis en eksponent), en vermenigvuldig die som met daardie eksponensiële uitdrukking. Jy kan dan  los en vermenigvuldig daardie antwoord met twee. Onthou dat dit moontlik is omdat `n vermenigvuldiging niks meer is as om `n optelling te herskryf nie, want
los en vermenigvuldig daardie antwoord met twee. Onthou dat dit moontlik is omdat `n vermenigvuldiging niks meer is as om `n optelling te herskryf nie, want  . Hier is `n paar voorbeelde:
. Hier is `n paar voorbeelde: 
2. Vermenigvuldig getalle met dieselfde basis deur die eksponente bymekaar te tel. As jy twee eksponente met dieselfde basis het, soos  , dan moet jy net die twee eksponente met dieselfde basis byvoeg. Dus,
, dan moet jy net die twee eksponente met dieselfde basis byvoeg. Dus, . As jy dit `n bietjie vreemd vind, verdeel dit in kleiner dele om te verstaan hoe die stelsel werk:
. As jy dit `n bietjie vreemd vind, verdeel dit in kleiner dele om te verstaan hoe die stelsel werk:
 , dan moet jy net die twee eksponente met dieselfde basis byvoeg. Dus,
, dan moet jy net die twee eksponente met dieselfde basis byvoeg. Dus, . As jy dit `n bietjie vreemd vind, verdeel dit in kleiner dele om te verstaan hoe die stelsel werk:
. As jy dit `n bietjie vreemd vind, verdeel dit in kleiner dele om te verstaan hoe die stelsel werk:






3. Vermenigvuldig `n eksponensiële getal verhoog tot `n ander mag, soos ( X 2 ) 5  . As jy `n getal tot `n sekere mag verhoog, en die geheel word tot `n sekere mag verhoog, vermenigvuldig net die twee eksponente. Dus,
. As jy `n getal tot `n sekere mag verhoog, en die geheel word tot `n sekere mag verhoog, vermenigvuldig net die twee eksponente. Dus,  . As jy deurmekaar raak, dink weer wat hierdie simbole eintlik beteken.
. As jy deurmekaar raak, dink weer wat hierdie simbole eintlik beteken.  beteken net jy
beteken net jy  Vermenigvuldig 5 keer met homself, dus:
Vermenigvuldig 5 keer met homself, dus:
 . As jy `n getal tot `n sekere mag verhoog, en die geheel word tot `n sekere mag verhoog, vermenigvuldig net die twee eksponente. Dus,
. As jy `n getal tot `n sekere mag verhoog, en die geheel word tot `n sekere mag verhoog, vermenigvuldig net die twee eksponente. Dus,  . As jy deurmekaar raak, dink weer wat hierdie simbole eintlik beteken.
. As jy deurmekaar raak, dink weer wat hierdie simbole eintlik beteken.  beteken net jy
beteken net jy  Vermenigvuldig 5 keer met homself, dus:
Vermenigvuldig 5 keer met homself, dus:



4. Dink aan negatiewe eksponente as breuke, of die wederkerige van die getal. Weet nie wat `n wederkerigheid is nie, geen probleem nie. As jy te doen het met `n negatiewe eksponent, soos  , maak dan die eksponent positief en plaas dit as die noemer onder een, wat lei tot
, maak dan die eksponent positief en plaas dit as die noemer onder een, wat lei tot  . Hier is `n paar bykomende voorbeelde:
. Hier is `n paar bykomende voorbeelde:
 , maak dan die eksponent positief en plaas dit as die noemer onder een, wat lei tot
, maak dan die eksponent positief en plaas dit as die noemer onder een, wat lei tot  . Hier is `n paar bykomende voorbeelde:
. Hier is `n paar bykomende voorbeelde:


5. Verdeel twee getalle met dieselfde basis deur die eksponente af te trek. Deling is die teenoorgestelde van vermenigvuldiging, en hoewel hulle nie presies as teenoorgesteldes opgelos word nie, is hulle hier. As jy met die vergelyking te doen het  , trek net die boonste eksponent van die onderste een af, en laat die basis soos dit is. Dus,
, trek net die boonste eksponent van die onderste een af, en laat die basis soos dit is. Dus,  , of 16.
, of 16.
 , trek net die boonste eksponent van die onderste een af, en laat die basis soos dit is. Dus,
, trek net die boonste eksponent van die onderste een af, en laat die basis soos dit is. Dus,  , of 16.
, of 16. , herskryf word as
, herskryf word as  . Negatiewe eksponente vorm breuke.
. Negatiewe eksponente vorm breuke.
6. Probeer `n paar oefenoefeninge om gewoond te raak om met maggetalle te werk. Die volgende oefeninge oefen alles wat tot dusver bespreek is. Vir die antwoord, kies net die reël wat die probleem bevat.
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Onthou dat `n getal sonder `n mag `n eksponent van 1 het
Onthou dat `n getal sonder `n mag `n eksponent van 1 het =
= 
 =
= 
Metode 3 van 3: Los breuke as maggetalle op

1. Behandel breuke in die vorm van maggetalle, soos X 1 2  as `n vierkantswortel.
as `n vierkantswortel.  is in werklikheid presies dieselfde as
is in werklikheid presies dieselfde as  . Dit is waar, ongeag die noemer van die breuk, dus
. Dit is waar, ongeag die noemer van die breuk, dus  word die kwadratiese wortel van x, ook geskryf as
word die kwadratiese wortel van x, ook geskryf as ![Oplossing van eksponente {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
.
 as `n vierkantswortel.
as `n vierkantswortel.  is in werklikheid presies dieselfde as
is in werklikheid presies dieselfde as  . Dit is waar, ongeag die noemer van die breuk, dus
. Dit is waar, ongeag die noemer van die breuk, dus  word die kwadratiese wortel van x, ook geskryf as
word die kwadratiese wortel van x, ook geskryf as ![Oplossing van eksponente {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
. - Wortels is die omgekeerde van eksponente. Byvoorbeeld, as jy die antwoord van neem
na die vierde mag, dan kom jy terug na
, en so kan
ook geskryf word as
. Nog `n voorbeeld is
en toe
en dus
.

2. Maak die teller `n normale eksponent vir `n gemengde breuk. kan onmoontlik lyk, maar is maklik as jy onthou hoe eksponente vermenigvuldig word. Maak die basis `n vierkantswortel, soos `n gewone breuk, en verhef die hele ding tot die mag boaan die breuk. As jy dit moeilik vind om dit te onthou, gaan weer deur die teorie. Uiteindelik geld dit
kan onmoontlik lyk, maar is maklik as jy onthou hoe eksponente vermenigvuldig word. Maak die basis `n vierkantswortel, soos `n gewone breuk, en verhef die hele ding tot die mag boaan die breuk. As jy dit moeilik vind om dit te onthou, gaan weer deur die teorie. Uiteindelik geld dit  net gelyk
net gelyk  Byvoorbeeld:
Byvoorbeeld:
 kan onmoontlik lyk, maar is maklik as jy onthou hoe eksponente vermenigvuldig word. Maak die basis `n vierkantswortel, soos `n gewone breuk, en verhef die hele ding tot die mag boaan die breuk. As jy dit moeilik vind om dit te onthou, gaan weer deur die teorie. Uiteindelik geld dit
kan onmoontlik lyk, maar is maklik as jy onthou hoe eksponente vermenigvuldig word. Maak die basis `n vierkantswortel, soos `n gewone breuk, en verhef die hele ding tot die mag boaan die breuk. As jy dit moeilik vind om dit te onthou, gaan weer deur die teorie. Uiteindelik geld dit  net gelyk
net gelyk  Byvoorbeeld:
Byvoorbeeld:

![Oplossing van eksponente x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Oplossing van eksponente ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)

3. Jy kan breuke optel, aftrek en vermenigvuldig in die vorm van maggetalle – net soos jy gewoonlik sou doen. Dit is baie makliker om die eksponente op te tel of af te trek voordat hulle opgelos of omgeskakel word na vierkantswortels. As die basis dieselfde is en die eksponent dieselfde is, kan jy hulle net optel en aftrek. As net die basis dieselfde is, dan kan jy die eksponente soos gewoonlik vermenigvuldig en deel, solank jy in ag neem hoe om breuke op te tel en af te trek. Byvoorbeeld:


Wenke
- Die meeste sakrekenaars het `n knoppie vir eksponente - druk nadat jy die basis ingevoer het - om kraggetalprobleme op te los.Gewoonlik lyk dit soos `n ^ of x^y.
- `Vereenvoudig` in wiskunde beteken doen die wysigings wat nodig is om die eenvoudigste vorm van die betrokke uitdrukkings te kry.
- 1 is die identiteitselement van eksponente. Dit beteken dat enige reële getal verhoog tot die mag 1 (tot die eerste mag) die getal self is, byvoorbeeld:
Ook, 1 is die identiteitselement van vermenigvuldiging (1 as vermenigvuldiger, soos
), en van afdeling (1 as dividend, soos
.
- Die basis nul tot nul (0) is ongedefinieerd (Engels: dne, bestaan nie). Rekenaars of sakrekenaars sal dan `n `fout` gee. Onthou dat enige nie-nul getal verhef tot die mag 0 altyd gelyk is aan 1,
- Byvoorbeeld, hoër wiskunde vir denkbeeldige getalle is,
, waardeur
; e is `n irrasionele, kontinue konstante gelyk aan 2,71828..., en a is `n arbitrêre konstante. Die bewys kan gevind word in die meeste hoër wiskunde boeke.
Waarskuwings
- `n Eksponensiële toename veroorsaak dat die produk vinniger en vinniger styg, sodat die antwoord verkeerd kan voorkom as dit korrek is. (Kontroleer dit deur byvoorbeeld `n eksponensiële funksie te teken.: 2, as x `n reeks verskillende waardes het).
Artikels oor die onderwerp "Oplossing van eksponente"
Оцените, пожалуйста статью
Gewilde