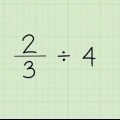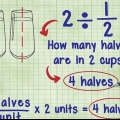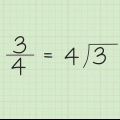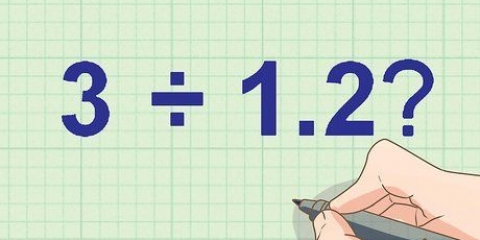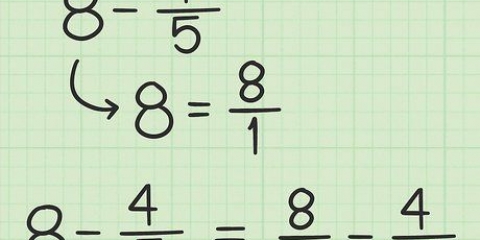Byvoorbeeld: die inverse (die inverse) van  is
is  .
. 
Byvoorbeeld: 

Byvoorbeeld:  kan tot die gemengde getal vereenvoudig word
kan tot die gemengde getal vereenvoudig word  .
. 

Byvoorbeeld, as jy deel deur  , dan dui die 4 in die noemer aan dat jy die geheel in vier gelyke dele moet verdeel.
, dan dui die 4 in die noemer aan dat jy die geheel in vier gelyke dele moet verdeel. 
Byvoorbeeld: stel jou deel 5 voor  , dan kleur jy driekwart in `n ander kleur vir elke groep. Let daarop dat baie groepe twee kwarte in een geheel en een kwart in `n ander geheel sal bevat.
, dan kleur jy driekwart in `n ander kleur vir elke groep. Let daarop dat baie groepe twee kwarte in een geheel en een kwart in `n ander geheel sal bevat. 
Byvoorbeeld, jy het ses groepe van  moet die vyf sirkels maak.
moet die vyf sirkels maak. 
Byvoorbeeld: na die verdeling van die vyf vorms in groepe van  , het jy twee kwartiere, of
, het jy twee kwartiere, of  oor. Aangesien `n hele groep uit drie stukke bestaan, en jy het twee stukke, is jou breuk
oor. Aangesien `n hele groep uit drie stukke bestaan, en jy het twee stukke, is jou breuk  .
. 
Byvoorbeeld:  .
. 

Maak `n breuk van 16 deur dit `n teller te maak met die noemer 1:  .
. Vind die wederkerige van die breuk deur die teller en noemer om te keer:  word
word  .
. Vermenigvuldig die twee breuke saam:  .
. Vereenvoudig, indien nodig:  .
. 
Trek nege sirkels om die nege blikkies voor te stel. Omdat sy  eet op `n slag, verdeel elke sirkel in derdes.
eet op `n slag, verdeel elke sirkel in derdes. Kleur die groepe van in  .
. Tel die aantal volledige groepe. Dit moet 13 wees. Interpreteer die oorblywende stukke. Daar is een stuk oor, en dit is  . Want `n hele groep
. Want `n hele groep  is, jy het `n halwe groep oor. So die breuk is
is, jy het `n halwe groep oor. So die breuk is  .
. Kombineer die aantal groepe heelgetalle en breuke om jou finale antwoord te vind:  .
.
Deling van 'n heelgetal deur 'n breuk
Inhoud
As jy `n heelgetal deur `n breuk wil deel, bereken jy eintlik hoeveel `groepe` van die breuk in die geheel ingaan. Die standaard manier om `n heelgetal deur `n breuk te deel, is om die heelgetal met die wederkerige van die breuk te vermenigvuldig. Jy kan ook `n grafiek skep om hierdie berekening te help visualiseer.
Trappe
Metode 1 van 3: Vermenigvuldig met die inverse

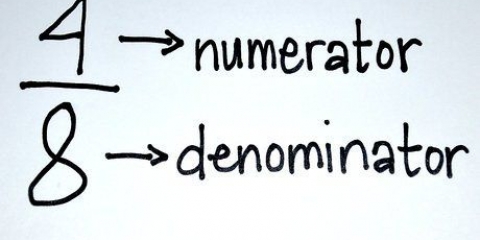
1. Skakel die heelgetal om na `n breuk. Jy doen dit deur die heelgetal in die teller van `n breuk te verander. Maak die noemer 1.
- Byvoorbeeld: Bereken jou
, dan verander jy eers
in
.

2. Vind die wederkerige van die breuk. Die wederkerigheid van `n getal is gelyk aan die inverse van daardie getal. Om die wederkerigheid van `n breuk te vind, ruil die teller en noemer om.
 is
is  .
.
3. Vermenigvuldig die twee breuke. Om breuke te vermenigvuldig, vermenigvuldig eers die tellers met mekaar. Vermenigvuldig dan die noemers saam. Die produk van die twee breuke is gelyk aan die kwosiënt van jou oorspronklike deelprobleem.


4. Vereenvoudig, indien nodig. As jy `n onbehoorlike breuk het (m.a.w. die teller is groter as die noemer), kan die probleem jou vra om dit na `n gemengde getal te verander. Normaalweg sal die verklaring vra vir om breuke te vereenvoudig tot die laagste terme.
 kan tot die gemengde getal vereenvoudig word
kan tot die gemengde getal vereenvoudig word  .
.Metode 2 van 3: Teken `n diagram

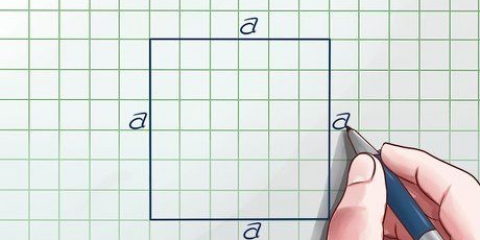
1. Teken vorms wat die heelgetal verteenwoordig. Jou vorm moet in gelyke groepe verdeel kan word, soos `n vierkant of `n sirkel. Teken die vorms so groot dat jy dit in kleiner stukke kan verdeel.
- Byvoorbeeld: in die berekening
, sal jy vyf sirkels teken.

2. Deel elke hele vorm deur die noemer van die breuk. Die noemer van `n breuk sê vir jou in hoeveel dele `n hele vorm verdeel is. Verdeel elke hele vorm in sy dele soos aangedui deur die breuk.
 , dan dui die 4 in die noemer aan dat jy die geheel in vier gelyke dele moet verdeel.
, dan dui die 4 in die noemer aan dat jy die geheel in vier gelyke dele moet verdeel.
3. Skakeer die groepe wat die breuk verteenwoordig. Aangesien jy die heelgetal deur die breuk deel, sien jy hoeveel groepe van die breuk in die heelgetal is. So dui jy eers die groepe aan. Dit kan nuttig wees om elke groep `n ander kleur te gee, aangesien sommige groepe dele in twee verskillende heelvorms het. Laat die oorblywende stukke leeg.
 , dan kleur jy driekwart in `n ander kleur vir elke groep. Let daarop dat baie groepe twee kwarte in een geheel en een kwart in `n ander geheel sal bevat.
, dan kleur jy driekwart in `n ander kleur vir elke groep. Let daarop dat baie groepe twee kwarte in een geheel en een kwart in `n ander geheel sal bevat.
4. Tel die aantal hele groepe. Dit sal jou die heelgetal van jou antwoord gee.
 moet die vyf sirkels maak.
moet die vyf sirkels maak.
5. Interpreteer die oorblywende stukke. Vergelyk die aantal stukke wat jy met `n hele groep oor het. Die breuk van `n groep wat jy oor het, dui die breuk van jou antwoord aan. Wees versigtig om nie die aantal stukke wat jy het te vergelyk met die aantal stukke wat jy het met `n hele vorm nie, want dit sal jou die verkeerde breuk gee.
 , het jy twee kwartiere, of
, het jy twee kwartiere, of  oor. Aangesien `n hele groep uit drie stukke bestaan, en jy het twee stukke, is jou breuk
oor. Aangesien `n hele groep uit drie stukke bestaan, en jy het twee stukke, is jou breuk  .
.
6. Skryf die antwoord neer. Kombineer die groepe van die heelgetal met die groepe van die breuk om die kwosiënt van jou oorspronklike delingsom te vind.
 .
.Metode 3 van 3: Voorbeeld van probleme met oplossings

1. Los op: Hoe dikwels doen  in
in  ?
?
 in
in  ?
? - Omdat die opdrag vra hoeveel groepe van
gaan in 8 is dit `n verdelingsom.
- Maak `n breuk van 8 deur dit `n teller te maak met noemer 1:
.
- Vind die wederkerige van die breuk deur die teller en noemer om te keer:
word
.
- Vermenigvuldig die twee breuke saam:
.
- Vereenvoudig, indien nodig:
.

2. Los op: .
.
 .
. .
. word
word  .
. .
. .
.
3. Los die volgende probleem op deur `n diagram te teken. Rufus het nege blikkies boontjies. Sy eet elke dag  n blikkie. Vir hoeveel dae het sy blikkies?
n blikkie. Vir hoeveel dae het sy blikkies?
 n blikkie. Vir hoeveel dae het sy blikkies?
n blikkie. Vir hoeveel dae het sy blikkies? eet op `n slag, verdeel elke sirkel in derdes.
eet op `n slag, verdeel elke sirkel in derdes. .
. . Want `n hele groep
. Want `n hele groep  is, jy het `n halwe groep oor. So die breuk is
is, jy het `n halwe groep oor. So die breuk is  .
. .
.Artikels oor die onderwerp "Deling van 'n heelgetal deur 'n breuk"
Оцените, пожалуйста статью
Soortgelyk
Gewilde