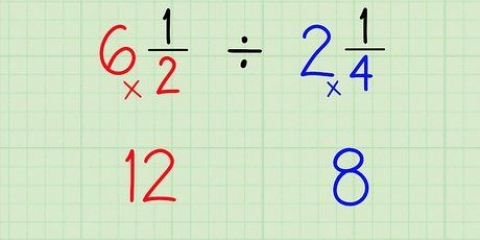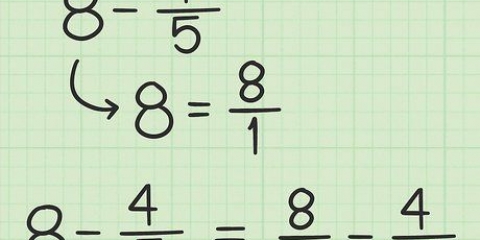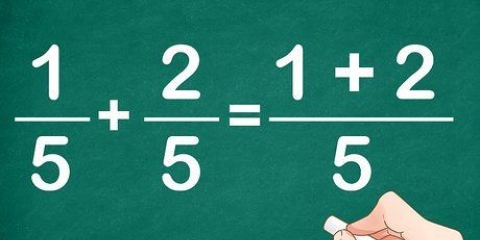Los ekwivalente breuke op: 8 stappe (met prente)

Inhoud

Trappe
- Metode 1 van 2: Skep ekwivalente breuke
- Metode 2 van 2: Los ekwivalente breuke met veranderlikes op
Wenke
Waarskuwings

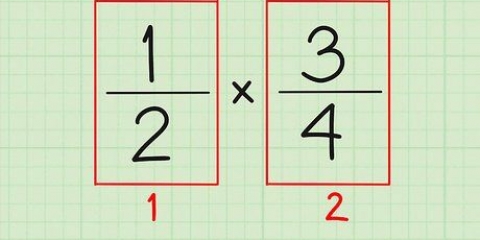
Twee breuke is "ekwivalent" as hulle dieselfde waarde het. Byvoorbeeld, die breuke 1/2 en 2/4 is ekwivalent omdat 1 oor 2 dieselfde waarde het as 2 oor 4 (0,5 in desimale vorm). Om te weet hoe om `n breuk na `n ander, dog ekwivalente breuk om te skakel, is `n noodsaaklike wiskunde wat jy nodig het, van basiese algebra tot gevorderde wiskunde. Kyk na Stap 1 om te begin!

Trappe

Metode 1 van 2: Skep ekwivalente breuke

Prent getiteld Doen ekwivalente breuke Stap 1

1. Vermenigvuldig die teller en noemer van `n breuk met dieselfde getal om `n ekwivalente breuk te kry. Twee breuke wat verskil, maar per definisie ekwivalent het, tellers en noemers wat veelvoude van mekaar is. Met ander woorde, vermenigvuldiging van die teller en noemer van `n breuk met dieselfde getal sal `n ekwivalente breuk produseer. Alhoewel die getalle in hierdie nuwe breuk verskil, het dit steeds dieselfde waarde.

Byvoorbeeld, as ons die breuk 4/8 neem en beide die teller en noemer met 2 vermenigvuldig, kry ons (4×2)/(8×2) = 8/16. Hierdie twee breuke is ekwivalent.

(4×2)/(8×2) is in wese dieselfde as 4/8 × 2/2. Onthou wanneer ons twee breuke vermenigvuldig, doen ons dit so - teller maal teller en noemer maal noemer. Let daarop dat 2/2 gelyk is aan 1. Dit is dus maklik om te sien hoekom 4/8 gelyk is aan 8/16 - die tweede breuk is die eerste breuk vermenigvuldig met 2!

2. Deel die teller en noemer of `n breuk deur dieselfde getal om `n ekwivalente breuk te kry. Soos vermenigvuldiging, kan deling ook gebruik word om `n nuwe breuk gelykstaande aan die gegewe breuk te skep. Deel net die teller en noemer van `n breuk deur dieselfde getal om `n ekwivalente breuk te kry. Daar is `n voorbehoud hier - die resulterende breuk moet bestaan uit heelgetalle in beide die teller en noemer om geldig te wees.

Byvoorbeeld, kom ons neem weer 4/8. As ons, in plaas van om te vermenigvuldig, beide die teller en die noemer deur 2 deel, kry ons (4 2)/(8 ÷ 2) = 2/4. 2 en 4 is albei heelgetalle, so hierdie ekwivalente breuk is geldig.

Prent getiteld Doen ekwivalente breuke Stap 2

3. Vereenvoudig jou breuk deur die grootste gemene deler (GGD) te gebruik. Enige gegewe breuk het `n oneindige aantal ekwivalente breuke - jy kan die teller en noemer vermenigvuldig met enige heelgetal, groot of klein om `n ekwivalente breuk te kry. Maar die eenvoudigste vorm van `n gegewe breuk is gewoonlik die een met die kleinste terme. In daardie geval is die teller en noemer albei so klein as moontlik - hulle kan nie meer deur enige heelgetal gedeel word om die term nog kleiner te maak nie. Om `n breuk te vereenvoudig, deel ons beide die teller en noemer deur die grootste gemene deler.

Die grootste gemene deler (GGD) van die teller en noemer is die grootste heelgetal waarmee beide teller en noemer deelbaar is. So in ons 4/8 voorbeeld, want 4 is die grootste deler van beide 4 en 8, deel ons die teller en noemer van ons breuk deur 4 om die eenvoudigste terme te kry. (4 4)/(8 ÷ 4) = 1/2.

Prent getiteld Doen ekwivalente breuke Stap 8

4. As jy wil, skakel gemengde getalle om na onbehoorlike breuke om omskakeling makliker te maak. Natuurlik sal nie elke breuk wat jy teëkom so maklik wees om te vereenvoudig soos 4/8 nie. Byvoorbeeld, gemengde getalle (bv. 1 3/4, 2 5/8, 5 2/3, ens.) kan hierdie omskakeling `n bietjie moeiliker maak. As jy `n breuk van `n gemengde getal wil maak, kan jy dit op twee maniere doen: maak die gemengde getal `n onbehoorlike breuk, en gaan dan voort, of hou die gemengde getal en gee `n gemengde getal as antwoord.

Om `n onbehoorlike breuk om te skakel, vermenigvuldig die heelgetal van die gemengde getal met die noemer van die breuk en tel dan die produk by die teller. Byvoorbeeld, 1 2/3 = ((1 × 3) + 2)/3 = 5/3. Dan kan jy dit weer omskakel indien nodig. Byvoorbeeld, 5/3 × 2/2 = 10/6, steeds dieselfde as 1 2/3.

Dit is egter nie nodig om `n onbehoorlike breuk om te skakel nie. Ons kan die heelgetal ignoreer en net die breuk omskakel en dan die heelgetal daarby voeg. Byvoorbeeld, by 3 4/16 kyk ons net na 4/16. 4/16 ÷ 4/4 = 1/4. So nou tel ons weer die heelgetal by en kry `n nuwe gemengde getal, 3 1/4.

5. Moet nooit optel of aftrek om ekwivalente breuke te kry nie. Wanneer breuke na hul ekwivalente vorm omgeskakel word, is dit belangrik om te onthou dat die enigste bewerkings wat jy toepas, vermenigvuldiging en deling is. Moet nooit optel of aftrek gebruik nie. Vermenigvuldiging en deling werk om ekwivalente breuke te kry, want hierdie bewerkings is eintlik vorme van die getal 1 (2/2, 3/3, ens.)en gee antwoorde wat gelyk is aan die breuk waarmee jy begin het. Optelling en aftrekking het nie hierdie vermoë nie.

Byvoorbeeld, hierbo het ons gevind dat 4/8 ÷ 4/4 = 1/2 . As ons eerder 4/4 hierby gevoeg het, sou ons `n heeltemal ander antwoord gekry het. 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 of 3/2, en nie een hiervan is gelyk aan 4/8 nie.

Metode 2 van 2: Los ekwivalente breuke met veranderlikes op

1. Gebruik kruisvermenigvuldiging om breuk-ekwivalensieprobleme op te los. `n Moeilike tipe algebra-probleem wat met ekwivalente breuke handel, behels vergelykings met twee breuke, waar een of albei `n veranderlike bevat. In gevalle soos hierdie weet ons dat hierdie breuke ekwivalent is omdat hulle die enigste terme aan weerskante van die gelyketeken van `n vergelyking is, maar dit is nie altyd duidelik hoe om die veranderlike op te los nie. Gelukkig kan ons met kruiselings vermenigvuldig, hierdie tipe probleem oplos sonder enige probleme.

Kruisvermenigvuldiging is presies hoe dit klink - jy vermenigvuldig op `n kruismanier oor die gelykheidsteken. Met ander woorde, jy vermenigvuldig die teller van een breuk met die noemer van die ander breuk en omgekeerd. Dan los jy die vergelyking verder op.
Byvoorbeeld, ons het die vergelyking 2/x = 10/13. Kruisvermenigvuldig nou: vermenigvuldig 2 met 13 en 10 met x, en werk die vergelyking verder uit:

2×13 = 26
10 × x = 10 x
10x = 26. Nou werk ons die vergelyking verder uit. x = 26/10 = 2.6

2. Gebruik kruisvermenigvuldiging op dieselfde manier as meerveranderlike vergelykings of veranderlike uitdrukkings. Een van die beste kenmerke van kruisvermenigvuldiging is dat dit amper dieselfde werk of jy nou met twee eenvoudige of komplekse breuke te doen het. Byvoorbeeld, as beide breuke veranderlikes bevat, sal niks verander nie - jy sal net van hierdie veranderlikes moet ontslae raak. Net so, as die tellers of noemers van jou breukveranderlike uitdrukkings bevat, net "voortgaan om te vermenigvuldig" deur die verspreidingseienskap te gebruik en op te los soos jy gewoonlik doen.

Gestel ons het byvoorbeeld die vergelyking ((x + 3)/2) = ((x + 1)/4). In hierdie geval los ons dit op deur kruisvermenigvuldiging:

(x + 3) × 4 = 4x + 12

(x + 1) × 2 = 2x + 2

2x + 2 = 4x + 12

2 = 2x + 12

-10 = 2x

-5 = x

3. Gebruik tegnieke om polinome op te los. Kruisvermenigvuldiging werk nie altyd `n resultaat wat jy met eenvoudige algebra kan oplos. As jy met veranderlike terme te doen het, sal jy vinnig `n kwadratiese vergelyking of ander polinoom kry as gevolg daarvan. In sulke gevalle gebruik jy byvoorbeeld kwadraat en/of die vierkantsformule.

Byvoorbeeld, ons neem die vergelyking ((x +1)/3) = (4/(2x - 2)). Eerste kruis vermenigvuldig:

(x + 1) × (2x - 2) = 2x + 2x -2x - 2 = 2x - 2

4×3 = 12

2x - 2 = 12. Op hierdie punt wil ons dit omskakel na `n kwadratiese vergelyking (ax + bx + c = 0) deur 12 van beide kante af te trek, wat 2x - 14 = 0 gee. Nou gebruik ons die formule (x = (-b +/- √(b - 4ac))/2a) om die waarde van x te vind:

x = (-b +/- √(b - 4ac))/2a. In ons vergelyking, 2x - 14 = 0, a = 2, b = 0, en c = -14.

x = (-0 +/- √(0 - 4(2)(-14))))/2(2)

x = (+/- √( 0 - -112))/2(2)

x = (+/- √(112))/2(2)

x = (+/- 10.58/4)

x = +/- 2.64 Op hierdie punt kontroleer ons ons antwoord deur 2.64 en -2.64 in die oorspronklike kwadratiese vergelyking te vervang.

Wenke

Om breuke na `n ekwivalente vorm om te skakel is eintlik soos om met `n breuk soos 2/2 of 5/5 te vermenigvuldig. Aangesien dit uiteindelik gelyk is aan 1, bly die waarde van die breuk dieselfde.