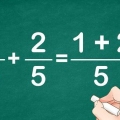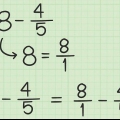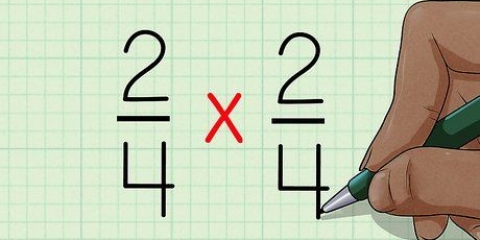Bestel breuke volgens grootte

Inhoud

Trappe
Wenke

Alhoewel dit maklik is om heelgetalle soos 1, 3 en 8 volgens grootte te orden, is dit nie altyd duidelik met breuke nie. As elke noemer gelyk is, kan jy hulle net soos heelgetalle orden, bv. 1/5, 3/5 en 8/5. In ander gevalle kan jy die breuke omskakel sodat hulle dieselfde noemer het, sonder om die waarde van die breuk te verander. Dit word makliker met oefening en jy kan `n paar handige truuks gebruik, beide wanneer jy twee breuke vergelyk of wanneer jy breuke bestel waar die teller groter is as die noemer, die ongepaste breuke soos 7/3.

Trappe

Metode 1 van 3: Orden van enige aantal breuke

Prent getiteld Bestel breuke van die minste tot die grootste Stap 1

1. Vind `n gelyke noemer vir alle breuke. Gebruik een van die volgende metodes om `n noemer te vind, of verminder die getal van `n breuk, wat jy kan gebruik om elke breuk in die lys te herskryf vir maklike vergelyking. Dit is wat jy noem a gemene deler, of die minste gemene deler as dit die kleinste moontlik is:

Vermenigvuldig elke noemer saam. Byvoorbeeld, as jy 2/3, 5/6 en 1/3 vergelyk, vermenigvuldig hierdie noemers saam: 3 x 6 = 18. Dit is `n eenvoudige metode, maar een wat dikwels `n baie groter getal tot gevolg het as die ander metodes, wat `n bietjie moeiliker is.
Of lys veelvoude van elke noemer in `n aparte kolom totdat `n getal wat meer dikwels voorkom uitstaan. Byvoorbeeld, by 2/3, 5/6 en 1/3 het jy `n lys veelvoude van 3:3, 6, 9, 12, 15, 18. Dan `n lys van veelvoude van 6: 6, 12, 18. Omdat 18 in beide lyste voorkom, gebruik daardie getal (Jy kan ook 12 gebruik, maar die voorbeelde hieronder neem aan dat jy 18 gebruik).

Prent getiteld Bestel breuke van die minste tot die grootste Stap 2

2. Skakel elke breuk om sodat hulle `n gelyke noemer het. Onthou dat as jy die teller en noemer van `n breuk met dieselfde getal vermenigvuldig, die waarde van die breuk dieselfde bly. Gebruik hierdie tegniek met elke breuk, een op `n slag, sodat elke breuk dieselfde noemer het. Probeer dit vir 2/3, 5/6 en 1/3, met die noemer 18:

18 ÷ 3 = 6, dus 2/3 = (2x6)/(3x6)=12/18

18 ÷ 6 = 3, dus 5/6 = (5x3)/(6x3)=15/18

18 ÷ 3 = 6, dus 1/3 = (1x6)/(3x6)=6/18

Prent getiteld Bestel breuke van die minste tot die grootste Stap 3

3. Rangskik die breuke volgens die tellers. Noudat alle breuke dieselfde noemer het, is hulle maklik om te vergelyk. Bestel hulle van die kleinste tot die grootste volgens die toonbank. Dit gee ons die volgende lys: 6/18, 12/18, 15/18.

Prent getiteld Bestel breuke van die minste tot die grootste Stap 4

4. Keer elke breuk terug na sy oorspronklike vorm. Laat die breuke in hierdie volgorde, maar skakel hulle terug na die oorspronklike breuk. Jy doen dit deur eenvoudig te onthou watter breuk aan watter behoort of deur die boonste en onderste getalle van die breuk weer te deel:

6/18 = (6 6)/(18 ÷ 6) = 1/3

12/18 = (12 6)/(18 ÷ 6) = 2/3

15/18 = (15 3)/(18 ÷ 3) = 5/6

Die antwoord is "1/3, 2/3, 5/6"

Metode 2 van 3: Orden van twee breuke met kruisvermenigvuldiging

Prent getiteld Bestel breuke van die minste tot die grootste Stap 5

1. Skryf die twee breuke langs mekaar neer. Vergelyk byvoorbeeld die breuk 3/5 en die breuk 2/3. Skryf hierdie langs mekaar: 3/5 aan die linkerkant en 2/3 aan die regterkant.

Prent getiteld Bestel breuke van die minste tot die grootste Stap 6

2. Vermenigvuldig die teller van die eerste breuk met die noemer van die tweede. Dus: 3 x 3 = 9.

Dit word kruisvermenigvuldiging genoem, want jy vermenigvuldig getalle diagonaal met mekaar.

Prent getiteld Bestel breuke van die minste tot die grootste stap 7

3. Skryf jou antwoord langs die eerste breuk neer. Skryf die produk van 3 x 3 = 9, langs die eerste breuk neer.

Prent getiteld Bestel breuke van die minste tot die grootste stap 8

4. Vermenigvuldig die teller van die tweede breuk met die noemer van die eerste. Om nou te sien watter is die grootste, vergelyk ons die antwoord met `n ander vermenigvuldiging. Vermenigvuldig hierdie twee getalle saam. In hierdie voorbeeld (ons vergelyk 3/5 en 2/3), vermenigvuldig ons 2 x 5.

Prent getiteld Bestel breuke van die minste tot die grootste Stap 9

5. Skryf die antwoord langs die tweede breuk neer. Skryf die resultaat van 2 x 5 =10 langs die tweede breuk neer.

Prent getiteld Bestel breuke van die minste tot die grootste Stap 10

6. Vergelyk die waardes van die uitkomste. As een waarde groter is as die ander, is die breuk langs die resultaat ook die grootste. Dus, aangesien 9 minder as 10 is, is 3/5 minder as 2/3.

Onthou om altyd die produk van die vermenigvuldiging langs die breuk waarvan jy die teller gebruik het te plaas.

Prent getiteld Bestel breuke van die minste tot die grootste stap 11

7. Hoe presies werk dit? Wat jy doen is om die breuke om te skakel sodat hulle albei dieselfde noemer het. Dit is dus wat kruisvermenigvuldiging eintlik doen! Dit slaan eintlik oor om die noemers neer te skryf, want in die geval van soortgelyke noemers hoef jy net die tellers te vergelyk. Dus soos volg, sonder die kort roete van kruisvermenigvuldiging:

3/5=(3x3)/(5x3)=9/15

2/3=(2x5)/(3x5)=10/15

9/15 is minder as 10/15

So 3/5 is minder as 2/3

Metode 3 van 3: Orden van breuke groter as een

Prent getiteld Bestel breuke van die minste tot die grootste stap 12

1. Gebruik hierdie metode vir breuke waar die teller groter is as die noemer. As die teller groter as die noemer is, dan is hierdie breuk groter as 1. 8/3 is `n voorbeeld hiervan. Jy kan dit ook gebruik vir breuke met dieselfde teller en noemer, soos 9/9. Hierdie is albei voorbeelde van "onbehoorlik" breuke.

Jy kan steeds die ander metodes vir hierdie breuke gebruik. Hierdie metode sal jou help om hierdie breuke beter te verstaan en kan `n bietjie vinniger wees.

Prent getiteld Bestel breuke van die minste tot die grootste stap 13

2. Skakel enige onbehoorlike breuk om na `n gemengde breuk. Maak dit `n kombinasie van `n heelgetal en `n breuk. Soms kan jy dit maklik uit jou kop doen. Byvoorbeeld, 9/9 = 1. In die moeiliker gevalle, gebruik lang deling om uit te vind hoeveel keer die noemer deelbaar is deur die teller. Enige res van die lang verdeling bly as `n breuk. Byvoorbeeld:

8/3 = 2 + 2/3

9/9 = 1

19/4 = 4 + 3/4

13/6 = 2 + 1/6

Prent getiteld Bestel breuke van die minste tot die grootste stap 14

3. Sorteer die gemengde getalle volgens die heelgetal. Noudat daar nie meer onbehoorlike breuke is nie, het jy `n beter idee van die grootte van elke getal. Ignoreer eers die breuke en sorteer elke gemengde getal volgens die heelgetal:

1 is die kleinste

2 + 2/3 en 2 + 1/6 (ons weet nog nie watter een groter as die ander is nie)

4 + 3/4 is die grootste

Prent getiteld Bestel breuke van die minste tot die grootste stap 15

4. Vergelyk die breuke in elke groep indien nodig. As jy veelvuldige gemengde getalle met dieselfde heelgetal het, soos 2 + 2/3 en 2 + 1/6, vergelyk die breuk van beide getalle om uit te vind watter is groter. In die voorbeeld vergelyk ons 2 + 2/3 en 2 + 1/6, en skakel die breuke om na dieselfde noemer:

2/3 = (2x2)/(3x2) = 4/6

1/6 = 1/6

4/6 is groter as 1/6

2 + 4/6 is groter as 2 + 1/6

2 + 2/3 is groter as 2 + 1/6

Prent getiteld Bestel breuke van die minste tot die grootste stap 16

5. Gebruik die resultaat om die lys gemengde getalle verder te sorteer. Die volgorde van die hele lys word nou: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.

Prent getiteld Bestel breuke van die minste tot die grootste stap 17

6. Skakel die gemengde getalle terug na die oorspronklike breuke. Hou die volgorde dieselfde, maar maak enige veranderinge ongedaan en herskryf die breuke as die oorspronklike onbehoorlike breuke: 9/9, 8/3, 13/6, 19/4.

Wenke

Wanneer `n groot aantal breuke in volgorde geplaas word, kan dit nuttig wees om klein groepies van 2, 3 of 4 breuke te vergelyk.
Alhoewel dit nuttig kan wees om die minste gemene deler te vind, sal enige gemene deler werk. Probeer om 2/3, 5/6 en 1/3 te rangskik met `n gemene deler van 36 en kyk of jy dieselfde resultaat kry.
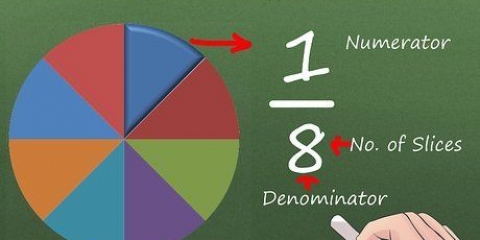
As die tellers almal dieselfde is, kan jy ook vinnig die breuke orden. Byvoorbeeld, 1/8 < 1/7 < 1/6 < 1/5. Dink hieraan asof dit `n pizza is: as jy van 1/2 na 1/8 gaan, sny jy die pizza in 8 stukke in plaas van 2 en die stukke is kleiner.