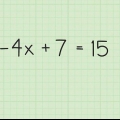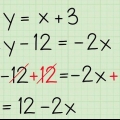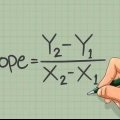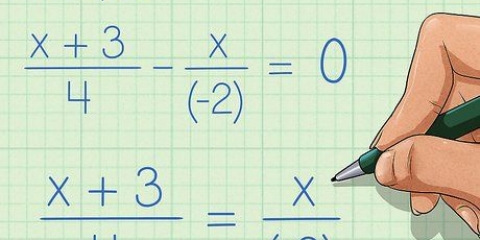Hoe om stelsels van vergelykings op te los deur twee veranderlikes te gebruik

Inhoud

Trappe
Wenke
Waarskuwings

In `n `stelsel van vergelykings` word jy gevra om twee of meer vergelykings gelyktydig op te los. Wanneer hierdie twee verskillende veranderlikes bevat, soos x en y, of a en b, kan dit met die eerste oogopslag moeilik wees om te sien hoe om dit op te los. Gelukkig, sodra jy weet wat om te doen, het jy net `n paar basiese wiskundevaardighede nodig (en soms `n bietjie kennis van breuke) om die probleem op te los. As dit vereis word, of as jy `n visuele leerder is, leer ook hoe om die vergelykings te teken. Om `n grafiek te teken (plot) kan nuttig wees om te `sien wat aangaan`, of om jou werk na te gaan, maar dit kan ook stadiger wees as die ander metodes en sal nie met alle stelsels vergelykings werk nie.

Trappe

Metode 1 van 3: Gebruik die substitusiemetode

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 1

1. Beweeg die veranderlikes na verskillende kante van die vergelyking. Hierdie `vervangingsmetode` begin deur `x op te los` (of enige ander veranderlike) in een van die vergelykings. Ons het byvoorbeeld die volgende vergelykings: 4x + 2j = 8 en 5x + 3x = 9. Kom ons kyk eers na die eerste vergelyking. Herrangskik deur 2y van elke kant af te trek, en jy kry: 4x = 8 - 2j.

Hierdie metode gebruik dikwels breuke op `n later stadium. Jy kan ook die uitskakelingsmetode hieronder gebruik as jy verkies om nie met breuke te werk nie.

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 2

2. Verdeel beide kante van die vergelyking om `op te los vir x`. Sodra jy die term x (of watter veranderlike jy ook al gebruik) aan die een kant van die vergelyking het, verdeel beide kante van die vergelyking om die veranderlike te isoleer. Byvoorbeeld:

4x = 8 - 2j

(4x)/4 = (8/4) - (2j/4)

x = 2 - y

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 3

3. Prop dit terug in die ander vergelyking. Maak seker om terug te keer na die Ander vergelyking, nie die een wat jy reeds gebruik het nie. In daardie vergelyking vervang jy die veranderlike wat jy opgelos het sodat net een veranderlike oorbly. Byvoorbeeld:

Jy weet nou dat: x = 2 - y.

Die tweede vergelyking, wat jy nog nie verander het nie, is: 5x + 3x = 9.

In die tweede vergelyking, vervang x met `2 - ½y`: 5(2 - ½j) + 3j = 9.

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 4

4. Los op vir die oorblywende veranderlike. Jy het nou `n vergelyking met net een veranderlike. Gebruik algemene algebra-tegnieke om daardie veranderlike op te los. As die veranderlikes mekaar kanselleer, gaan voort na die laaste stap. Andersins sal jy met `n antwoord op een van jou veranderlikes eindig:

5(2 - ½j) + 3j = 9

10 – (5/2)j + 3j = 9

10 – (5/2)j + (6/2)j = 9 (As jy nie hierdie stap verstaan nie, leer hoe om breuke by te voeg. Dit is dikwels, maar nie altyd nie, nodig met hierdie metode).

10 + j = 9

y = -1

y = -2

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 5

5. Gebruik die antwoord om die ander veranderlike op te los. Moenie die fout maak om die probleem halfpad klaar te maak nie. Jy sal die antwoord wat jy gekry het weer in een van die oorspronklike vergelykings moet invoer sodat jy vir die ander veranderlike kan oplos:

Jy weet nou dat: y = -2

Een van die oorspronklike vergelykings is: 4x + 2j = 8. (Albei vergelykings kan vir hierdie stap gebruik word).

Prop in -2 in plaas van y: 4x + 2(-2) = 8.

4x - 4 = 8

4x = 12

x = 3

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 6

6. Weet wat om te doen wanneer beide veranderlikes mekaar uitkanselleer. Wanneer jy x = 3y + 2 of `n soortgelyke antwoord in die ander vergelyking kry, dan probeer jy `n vergelyking met net een veranderlike kry. Soms eindig jy eerder met `n vergelyking sonder veranderlikes. Gaan jou werk dubbel na en maak seker dat jy die (herrangskik) eerste vergelyking in die tweede vergelyking vervang, nie die eerste vergelyking nie. As jy seker is dat jy geen foute gemaak het nie, sal jy een van die volgende resultate kry:

As jy eindig met `n vergelyking sonder veranderlikes en wat nie waar is nie (byvoorbeeld, 3 = 5), dan het die probleem geen oplossing nie. (As jy die vergelykings geteken het, sal jy sien dat hulle parallel is en nooit sny nie).

As jy eindig met `n vergelyking met geen veranderlikes, maar dié wel waar is (byvoorbeeld, 3 = 3), dan het die probleem `n oneindige aantal oplossings. Die twee vergelykings is presies gelyk aan mekaar. (As jy die twee vergelykings grafiek, sal jy sien dat hulle presies oorvleuel).

Metode 2 van 3: Gebruik die eliminasiemetode

1. Bepaal die veranderlike wat uitgeskakel moet word. Soms sal die vergelykings mekaar in `n veranderlike `uitskakel` sodra jy hulle bymekaar tel. Byvoorbeeld, wanneer jy die vergelykings doen 3x + 2j = 11 en 5x - 2j = 13 kombineer, sal die `+2y` en `-2y` mekaar uitskakel, met al `ys word uit die vergelyking verwyder. Kyk na die vergelykings in jou probleem om uit te vind of enige van die veranderlikes op hierdie manier uitgeskakel sal word. As geen van die veranderlikes uitgeskakel word nie, lees verder na die volgende stap vir advies.

Beeld getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 7

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 8

2. Vermenigvuldig `n vergelyking om `n veranderlike uit te skakel. (Slaan hierdie stap oor as die veranderlikes mekaar reeds uitgeskakel het). As geen van die veranderlikes in die vergelykings vanself uitgeskakel word nie, moet jy een van die vergelykings verander sodat hulle. Dit is die maklikste om te verstaan met `n voorbeeld:

Gestel jy het die stelsel van vergelykings 3x - y = 3 en -x + 2y = 4.

Kom ons verander die eerste vergelyking sodat die veranderlike y word uitgeskakel. (Jy kan dit ook doen vir X doen en kry dieselfde antwoord).

Die - jy` van die eerste vergelyking moet uitgeskakel word met die+ 2j ` in die tweede vergelyking. Ons kan dit doen deur - y om met 2 te vermenigvuldig.

Ons vermenigvuldig beide kante van die eerste vergelyking met 2, soos volg: 2(3x - y)=2(3), en dus 6x - 2j = 6. Nou sal - 2j val weg teen die +2j in die tweede vergelyking.

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 9

3. Kombineer die twee vergelykings. Om twee vergelykings te kombineer, voeg die linker- en regterkante bymekaar. As jy die vergelyking korrek geskryf het, behoort een van die veranderlikes teen die ander uit te kanselleer. Hier is `n voorbeeld wat dieselfde vergelykings as die laaste stap gebruik:

Jou vergelykings is: 6x - 2j = 6 en -x + 2y = 4.

Kombineer die linkerkante: 6x - 2y - x + 2y = ?

Kombineer die regte kante: 6x - 2y - x + 2y = 6 + 4.

Beeld getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 10

4. Los op vir die laaste veranderlike. Vereenvoudig die gekombineerde vergelyking, gebruik dan basiese algebra om die laaste veranderlike op te los. As daar geen veranderlikes oor is na vereenvoudiging nie, gaan oor na die laaste stap in hierdie afdeling. Andersins behoort jy `n eenvoudige antwoord op een van jou veranderlikes te kry. Byvoorbeeld:

Jy het: 6x - 2y - x + 2y = 6 + 4.

Groepeer die veranderlikes X en y met mekaar: 6x - x - 2y + 2y = 6 + 4.

Vereenvoudig: 5x = 10

Los op vir x: (5x)/5 = 10/5, sodat x = 2.

Beeld getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 11

5. Los op vir die ander veranderlikes. Jy het een veranderlike gevind, maar jy is nog nie heeltemal klaar nie. Vervang jou antwoord in een van die oorspronklike vergelykings sodat jy die ander veranderlike kan oplos. Byvoorbeeld:

Jy weet wat x = 2, en daardie een van jou oorspronklike vergelykings 3x - y = 3 is.

Prop 2 in, in plaas van x: 3(2) - y = 3.

Los op vir y in die vergelyking: 6 - j = 3

6 - j + j = 3 + j, so 6 = 3 + j

3 = j

Beeld getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 12

6. Weet wat om te doen as beide veranderlikes mekaar kanselleer. Soms lei die kombinasie van twee vergelykings tot `n vergelyking wat geen sin maak nie, of wat jou nie help om die probleem op te los nie. Kontroleer jou werk van die begin af, maar as jy nie `n fout gemaak het nie, skryf een van die volgende antwoorde:

As jou gekombineerde vergelyking geen veranderlikes het nie en nie waar is nie (soos 2 = 7), dan is daar geen oplossing nie wat geld vir beide vergelykings. (As jy albei vergelykings grafiek, sal jy sien dat hulle parallel is en nooit sny nie).

As jou gekombineerde vergelyking geen veranderlikes het nie en waar is (soos 0 = 0), dan is daar `n oneindige aantal oplossings. Die twee vergelykings is eintlik identies. (As jy dit op `n grafiek plaas, sal jy sien dat hulle heeltemal oorvleuel).

Metode 3 van 3: Teken die vergelykings in grafieke

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 13

1. Gebruik slegs hierdie metode wanneer gespesifiseer. Tensy jy `n rekenaar of `n grafiese sakrekenaar gebruik, kan baie stelsels vergelykings slegs ongeveer met hierdie metode opgelos word. Jou onderwyser of wiskunde handboek kan jou vra om hierdie metode te gebruik, so jy is waarskynlik vertroud met grafiese vergelykings soos lyne. Jy kan ook hierdie metode gebruik om te kyk of jou antwoorde van een van die ander metodes korrek is.

Die basiese idee is dat jy beide vergelykings grafiek en die punt bepaal waar hulle sny. Die x- en y-waardes op hierdie punt lewer die waarde van x en die waarde van y in die stelsel van vergelykings.

Beeld getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 14

2. Los beide vergelykings vir y op. Hou die twee vergelykings apart, gebruik algebra om elke vergelyking om te skakel in die vorm `y = __x + __`. Byvoorbeeld:

Die eerste vergelyking is: 2x + y = 5. Verander dit na: y = -2x + 5.

Die tweede vergelyking is: -3x + 6j = 0. Verander dit na 6j = 3x + 0, en vereenvoudig omy = ½x + 0.

Is beide vergelykings identies, dan word die hele lyn `n `kruising`. Skryf: oneindige oplossings.

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 15

3. Teken `n koördinaatstelsel. Teken op `n stuk grafiekpapier `n vertikale `y-as` en `n horisontale `x-as`. Begin by die punt waar die lyne sny, en benoem die nommers 1, 2, 3, 4, ens. op langs die y-as en weer regs langs die x-as. Benoem die nommers -1, -2, ens. langs die y-as af en links langs die x-as.

As jy nie grafiekpapier het nie, gebruik `n liniaal om seker te maak die getalle is eweredig gespasieer.

As jy groot getalle of desimale gebruik, moet jy dalk die grafiek skaal. (Byvoorbeeld 10, 20, 30 of 0.1, 0.2.0.3 in plaas van 1, 2, 3).

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 16

4. Trek die y-afsnit vir elke lyn. Sodra jy `n vergelyking in die vorm het y = __x + __ jy kan dit begin teken deur `n punt te teken waar die lyn die y-as sny. Dit is altyd op `n y-waarde, gelyk aan die laaste getal in hierdie vergelyking.

In die voorgenoemde voorbeelde, een reël (y = -2x + 5) in die y-as 5. Die ander lyn (y = ½x + 0) gaan deur die nulpunt 0. (Dit is die punte (0.5) en (0.0) in die grafiek).

Merk elkeen van die lyne met `n ander kleur, indien moontlik.

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 17

5. Gebruik die helling om voort te gaan om die lyne te trek. In die vorm y = __x + __, is die getal vir die x de gradiënt van die lyn af. Elke keer as x met een verhoog word, sal die y-waarde met die waarde van die helling toeneem. Gebruik hierdie inligting om die punt op die grafiek vir elke lyn te vind, wanneer x = 1. (Alternatiewelik, vervang x = 1 vir enige vergelyking en los op vir y).

In ons voorbeeld, die reël y = -2x + 5 `n helling van -2. By x = 1 val die lyn 2 afvanaf die punt x = 0. Trek die lynstuk tussen (0.5) en (1.3).

Die reël y = ½x + 0het `n helling van ½. By x = 1 gaan die lyn ½ op vanaf die punt x = 0. Trek die lynstuk tussen (0,0) en (1,½).

As die lyne dieselfde helling het die lyne sal nooit sny nie, so daar is geen oplossing vir die stelsel vergelykings nie. Skryf: geen oplossing nie.

Beeld getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 18

6. Gaan voort om die lyne te teken totdat hulle sny. Stop en kyk na jou grafiek. As die lyne reeds oor mekaar gekruis het, gaan voort na die volgende stap. Andersins neem jy `n besluit op grond van wat die lyne doen:

As die lyne na mekaar toe beweeg, sal jy voortgaan om punte in daardie rigting te teken.

As die lyne van mekaar wegbeweeg, gaan terug en teken punte in die ander rigting, begin by x = -1.

As die lyne nêrens naby mekaar is nie, spring vorentoe en stip meer verafgeleë punte, soos x = 10.

Prent getiteld Los stelsels van algebraïese vergelykings op wat twee veranderlikes bevat Stap 19

7. Vind die antwoord by die snypunt van die lyne. Sodra die twee lyne sny, is die x- en y-waardes op daardie punt die oplossing vir die probleem. As jy gelukkig is, sal die antwoord `n heelgetal wees. Byvoorbeeld, in ons voorbeelde sny die twee lyne (2.1) so is jou antwoord x = 2 en y = 1. In sommige stelsels vergelykings sal die lyne sny teen `n waarde tussen twee heelgetalle, en tensy jou grafiek uiters akkuraat is, sal dit moeilik wees om te sê waar dit is. As dit die geval is, kan jy `n antwoord gee soos: `x is tussen 1 en 2`. Jy kan ook die vervangingsmetode of eliminasiemetode gebruik om die presiese antwoord te vind.

Wenke

Jy kan jou werk nagaan deur die antwoorde terug te voer in die oorspronklike vergelykings. As die vergelykings waar is (byvoorbeeld, 3 = 3), dan is jou antwoord korrek.
In die eliminasiemetode moet jy soms `n vergelyking met `n negatiewe getal vermenigvuldig om `n veranderlike uit te skakel.

Waarskuwings

Hierdie metodes kan nie gebruik word wanneer jy met `n maggetal, soos x, handel nie. Vir meer inligting oor vergelykings van hierdie tipe het jy `n gids nodig vir die faktorisering van vierkante met twee veranderlikes.