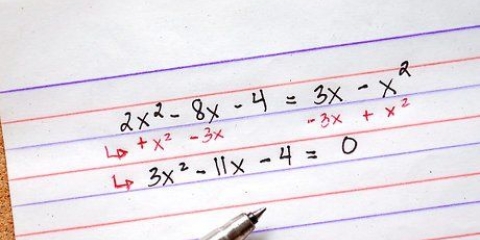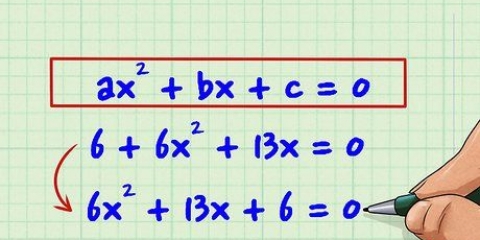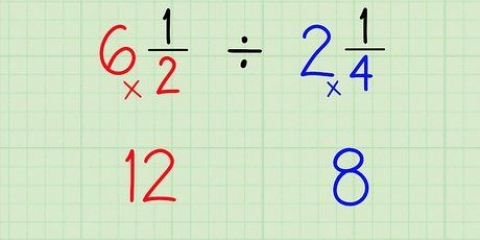Kruisvermenigvuldiging werk op algemene algebraïese beginsels. Rasionale uitdrukkings en ander breuke kan na gewone getalle omgeskakel word deur die noemers te vermenigvuldig. Kruisvermenigvuldiging is basies `n gerieflike, verkorte manier om beide kante van die vergelyking met die noemers van die breuke te vermenigvuldig. Glo jy dit nie? Probeer dit - jy sal dieselfde resultate sien nadat jy dit vereenvoudig het. 
Byvoorbeeld, as (x+3)/4 = x/(-2) jou oorspronklike rasionale uitdrukking was, dan word dit na kruisvermenigvuldiging gelyk aan -2(x+3) = 4x. Dit kan moontlik herskryf word as -2x - 6 = 4x. 
In ons voorbeeld is dit moontlik om beide kante van die vergelyking te deel deur -2, wat usx+3 = -2x gee. Deur x van beide kante van die gelykheidsteken af te trek, gee ons 3 = -3x. En laastens, deur beide kante deur -3 te deel, kry ons -1 = x, of ook x = -1. Nou het ons x gevind wat ons rasionale vergelyking oplos. 

Soms is die kleinste gemene veelvoud – die kleinste getal wat deur elkeen van die noemers deelbaar is – onmiddellik sigbaar. Byvoorbeeld, as jou uitdrukking soos x/3 + 1/2 = (3x+1)/6 lyk, dan is dit maklik om te sien dat die lcm deelbaar moet wees deur 3, 2 en 6, dus is dit gelyk aan 6. Maar meer dikwels is die LCF van `n rasionale vergelyking glad nie onmiddellik duidelik nie. In daardie gevalle, probeer die veelvoude van die grootste noemer totdat jy `n getal kry wat die veelvoude van die ander, kleiner noemers insluit. Dikwels is die LCF `n produk van twee noemers. Neem byvoorbeeld die vergelyking x/8 + 2/6 = (x - 3)/9, waar die lcm gelyk is aan 8*9 = 72. As een of meer van die noemers `n veranderlike bevat, is hierdie proses ietwat moeiliker, maar dit is beslis nie onmoontlik nie. In daardie gevalle is die LCF `n uitdrukking (met veranderlikes) waarin alle noemers heeltemal inpas, nie net `n enkele getal nie. As `n voorbeeld, die vergelyking 5/(x-1) = 1/x + 2/(3x), waar die lcg gelyk is aan 3x(x-1), want dit is volledig deelbaar deur enige noemer – deel deur (x- 1) ) gee 3x, deling deur 3x gee (x-1) en deling deur x gee 3(x-1). 
In ons voorbeeld kan ons x/3 met 2/2 vermenigvuldig om 2x/6 te kry en 1/2 met 3/3 vermenigvuldig om 3/6 te kry. 3x +1/6 het reeds `n 6 (LCM) as noemer, so ons kan dit met 1/1 vermenigvuldig of dit net los. In ons voorbeeld met veranderlikes in die noemers, is die hele proses `n bietjie meer ingewikkeld. Aangesien die lcc gelyk is aan 3x(x-1) vermenigvuldig ons enige rasionale uitdrukking met `n breuk wat 3x(x-1) as die noemer lewer. Ons vermenigvuldig 5/(x-1) met (3x)/(3x) en dit gee 5(3x)/(3x)(x-1), ons vermenigvuldig 1/x met 3(x-1)/3(x) -1) en dit gee 3(x-1)/3x(x-1) en ons vermenigvuldig 2/(3x) met (x-1)/(x-1) en dit gee uiteindelik 2(x-1)/ 3x (x-1). 
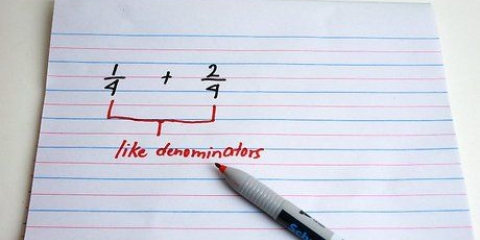
In ons voorbeeld, na vermenigvuldiging, deur 1 as `n breuk te wedden, kry ons 2x/6 + 3/6 = (3x+1)/6. Twee breuke kan bygevoeg word as hulle dieselfde noemer het, dus kan ons hierdie vergelyking skryf as (2x+3)/6 = (3x+1)/6 sonder om die waarde daarvan te verander. Vermenigvuldig beide kante met 6 om die noemers uit te kanselleer, en laat ons met 2x+3 = 3x+1. Trek hier 1 van beide kante af om 2x+2 = 3x te kry en trek 2x van albei kante af om 2 = x te kry, wat dan ook geskryf kan word as x = 2. In ons voorbeeld met veranderlikes in die noemers, die vergelyking na vermenigvuldiging van elke term met "1" gelyk aan 5(3x)/(3x)(x-1) = 3(x-1)/3x(x-1) + 2(x-1)/3x(x-1). Deur elke term met die lcm te vermenigvuldig, maak dit moontlik om die noemers uit te skakel, wat vir ons 5(3x) = 3(x-1) + 2(x-1) gee. Dit word verder uitgebrei as 15x = 3x - 3 + 2x -2, wat weer vereenvoudig kan word as 15x = x - 5. Deur x van beide kante af te trek, lewer 14x = -5, wat die finale antwoord kan vereenvoudig tot x = -5/14.
Los vergelykings met breuke op
Inhoud
`n Rasionele funksie is `n breuk met een of meer veranderlikes in die teller of noemer. `n Rasionele vergelyking is enige vergelyking wat ten minste een rasionale uitdrukking bevat. Soos gewone algebraïese vergelykings, kan rasionale uitdrukkings opgelos word deur dieselfde bewerking aan beide kante van die vergelyking toe te pas totdat die veranderlike aan die een kant van die gelykheidsteken geïsoleer is. Twee spesiale metodes, kruisvermenigvuldiging en die vind van die kleinste gemene veelvoud van die noemers, is veral nuttig om veranderlikes te isoleer en rasionale vergelykings op te los.
Trappe
Metode 1 van 2: Metode Een: Kruisvermenigvuldiging

1. Indien nodig, herrangskik die vergelyking om te verseker dat daar `n breuk aan beide kante van die gelyke-teken is. Kruisvermenigvuldiging is `n vinnige metode om rasionale vergelykings op te los. Ongelukkig werk hierdie metode net vir rasionale vergelykings wat presies een rasionale uitdrukking of breuk aan beide kante van die gelykteken het. As dit nie die geval is in jou vergelyking nie, dan het jy waarskynlik `n paar algebraïese bewerkings nodig om die terme op die regte plek te kry. Sommige rasionale vergelykings kan nie so maklik na die korrekte vorm omgeskakel word nie. Gebruik in daardie gevalle die metodes wat die kleinste gemene veelvoud van die noemers gebruik.
- Byvoorbeeld, die vergelyking (x + 3)/4 - x/(-2) = 0 kan maklik omgeskakel word na die korrekte vorm vir kruisvermenigvuldiging deur x/(-2) aan beide kante van die vergelyking by te tel, wat dit tot gevolg het lyk so: (x + 3)/4 = x/(-2).
- Onthou dat desimale en heelgetalle na breuke omgeskakel kan word deur dit as noemer 1 te gee. (x + 3)/4 - 2.5 = 5, kan byvoorbeeld herskryf word as (x + 3)/4 = 7.5/1, wat toelaat dat kruisvermenigvuldiging toegepas word.

2. Kruis Vermenigvuldig. Kruisvermenigvuldiging beteken eenvoudig om die teller van een breuk te vermenigvuldig met die noemer van die ander en omgekeerd. Vermenigvuldig die teller van die breuk links van die gelykheidsteken met die breuk regs. Herhaal met die teller aan die regterkant en die noemer van die breuk aan die linkerkant.

3. Maak die twee produkte gelyk aan mekaar. Na die kruisvermenigvuldiging bly jy oor met twee produkte. Maak hierdie twee terme gelyk en vereenvoudig hulle om die eenvoudigste terme aan beide kante van die vergelyking te laat.

4. Los op vir die veranderlike. Gebruik algebraïese bewerkings om die waarde van die veranderlike in die vergelyking te vind. Onthou dat as x aan beide kante van die gelyke-teken verskyn, jy `n x-term moet optel of aftrek om seker te maak dat daar net x-terme aan die een kant van die gelyke-teken is.
Metode 2 van 2: Metode Twee: Vind die kleinste gemene veelvoud (GKM) van die noemers

1. Probeer om te sien wanneer dit voor die hand liggend is om die kleinste gemene veelvoud van die noemers te vind. Die kleinste gemene veelvoud (LCM) van die noemers kan gebruik word om rasionale vergelykings te vereenvoudig, wat dit moontlik maak om die waardes van hul veranderlikes te vind. Om `n LCF te vind is `n goeie idee as die rasionale vergelyking nie maklik herskryf kan word in `n vorm waar daar net een breuk of rasionale uitdrukking aan elke kant van die gelyktekens is nie. Vir die oplossing van rasionale vergelykings met drie terme of meer, is LCF`s `n nuttige hulpmiddel. Maar vir die oplossing van rasionale vergelykings met slegs twee terme, is kruisvermenigvuldiging dikwels vinniger.

2. Ondersoek die noemer van elke breuk. Vind die kleinste getal wat deelbaar is deur enige noemer. Dit is die kgv van jou vergelyking.

3. Vermenigvuldig elke breuk in die rasionale vergelyking met 1. Om enige term met 1 te vermenigvuldig, kan sinloos lyk, maar hier is `n truuk. 1 kan as `n breuk geskryf word – bv. 2/2 en 3/3. Vermenigvuldig elke breuk in jou rasionale vergelyking met 1, skryf 1 elke keer as die getal of term vermenigvuldig met elke noemer om die LCF as `n breuk voor te stel.

4. Vereenvoudig en los op vir x. Noudat elke term in jou rasionale vergelyking dieselfde noemer het, is dit moontlik om die noemers uit die vergelyking te verwyder en vir die tellers op te los. Vermenigvuldig net beide kante van die vergelyking met die lcg om die noemers uit te skakel sodat jy net met die tellers oorbly. Nou het dit `n gereelde vergelyking geword wat jy vir die veranderlike kan oplos deur dit aan die een kant van die gelykheidsteken te isoleer.
Wenke
- Sodra jy die waarde van die veranderlike gevind het, kontroleer jou antwoord deur hierdie waarde in die oorspronklike vergelyking in te voeg. Sodra jy die veranderlike se waarde reg gekry het, behoort jy die vergelyking te kan vereenvoudig tot `n eenvoudige, geldige stelling, soos 1 = 1.
- Elke vergelyking kan as `n rasionele uitdrukking geskryf word; Sit dit net as teller bo die noemer 1. Dus kan die vergelyking x+3 geskryf word as (x+3)/1, albei het dieselfde waarde.
Artikels oor die onderwerp "Los vergelykings met breuke op"
Оцените, пожалуйста статью
Gewilde